
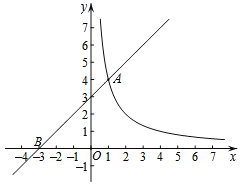
【题目】如图,在平面直角坐标系xOy中,直线y=x+3与函数y=![]() (x>0)的图象交于点A(1,m),与x轴交于点B.
(x>0)的图象交于点A(1,m),与x轴交于点B.
(1)求m,k的值;
(2)过动点P(0,n)(n>0)作平行于x轴的直线,交函数y=![]() (x>0)的图象于点C,交直线y=x+3于点D.
(x>0)的图象于点C,交直线y=x+3于点D.
①当n=2时,求线段CD的长;
②若CD≥OB,结合函数的图象,直接写出n的取值范围.
【答案】(1)m=4,k=4;(2)①CD=3;②0<n≤2或n≥3+![]() .
.
【解析】
(1)先利用一次函数解析式确定m的值得到A点坐标,然后把A点坐标代入y=![]() 得到k的值;
得到k的值;
(2)①利用C、D的纵坐标都为2得到C点和D点的横坐标,然后求两横坐标之差得到线段CD的长;
②先确定(﹣3,0),由于C、D的纵坐标都为n,根据一次函数和反比例函数图象上点的坐标特征可表示出C(![]() ,n),D(n﹣3,n),讨论:当点C在点D的右侧时,先利用CD=OB得到
,n),D(n﹣3,n),讨论:当点C在点D的右侧时,先利用CD=OB得到![]() ﹣(n﹣3)=3,解得n1=2,n2=﹣2(舍去),再结合图象可判断当0<n≤2时,CD≥OB;当点C在点D的左侧时,先利用CD=OB得到n﹣3﹣
﹣(n﹣3)=3,解得n1=2,n2=﹣2(舍去),再结合图象可判断当0<n≤2时,CD≥OB;当点C在点D的左侧时,先利用CD=OB得到n﹣3﹣![]() =3,解得n1=3+
=3,解得n1=3+![]() ,n2=3﹣
,n2=3﹣![]() (舍去),再结合图象可判断当n≥3+
(舍去),再结合图象可判断当n≥3+![]() 时,CD≥OB.
时,CD≥OB.
(1)∵直线y=x+3经过点A(1,m),
∴m=1+3=4,
∵反比例函数![]() 的图象经过点A(1,4),
的图象经过点A(1,4),
∴k=1×4=4;
(2)①当n=2时,点P的坐标为(0,2),
当y=2时,2=![]() ,解得x=2,
,解得x=2,
∴点C的坐标为(2,2),
当y=2时,x+3=2,解得x=﹣1,
∴点D的坐标为(﹣1,2),
∴CD=2﹣(﹣1)=3;
②当y=0时,x+3=0,解得x=﹣3,则B(﹣3,0)
当y=n时,n=![]() ,解得x=
,解得x=![]() ,
,
∴点C的坐标为(![]() ,n),
,n),
当y=n时,x+3=n,解得x=n﹣3,
∴点D的坐标为(n﹣3,n),
当点C在点D的右侧时,
若CD=OB,即![]() ﹣(n﹣3)=3,解得n1=2,n2=﹣2(舍去),
﹣(n﹣3)=3,解得n1=2,n2=﹣2(舍去),
∴当0<n≤2时,CD≥OB;
当点C在点D的左侧时,
若CD=OB,即n﹣3﹣![]() =3,解得n1=3+
=3,解得n1=3+![]() ,n2=3﹣
,n2=3﹣![]() (舍去),
(舍去),
∴当n≥3+![]() 时,CD≥OB,
时,CD≥OB,
综上所述,n的取值范围为0<n≤2或n≥3+![]() .
.
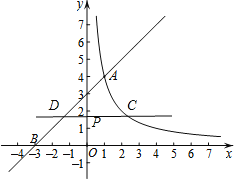


科目:初中数学 来源: 题型:
【题目】已知锐角∠AOB,如图,(1)在射线OA上取一点C,以点O为圆心,OC长为半径作![]() ,交射线OB于点D,连接CD;(2)分别以点C,D为圆心,CD长为半径作弧,两弧交于点P,连接CP,DP;(3)作射线OP交CD于点Q.根据以上作图过程及所作图形,下列结论中错误的是( )
,交射线OB于点D,连接CD;(2)分别以点C,D为圆心,CD长为半径作弧,两弧交于点P,连接CP,DP;(3)作射线OP交CD于点Q.根据以上作图过程及所作图形,下列结论中错误的是( )
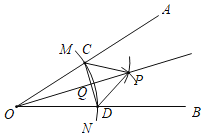
A.CP∥OBB.CP=2QCC.∠AOP=∠BOPD.CD⊥OP
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:在平面直角坐标系![]() 中,对于任意的实数
中,对于任意的实数![]() ,直线
,直线![]() 都经过平面内一个定点
都经过平面内一个定点![]() .
.
(1)求点![]() 的坐标.
的坐标.
(2)反比例函数![]() 的图象与直线
的图象与直线![]() 交于点
交于点![]() 和另外一点
和另外一点![]()
①求![]() 的值;
的值;
②当![]() 时,求
时,求![]() 的取值范围
的取值范围
查看答案和解析>>
科目:初中数学 来源: 题型:
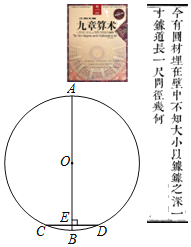
【题目】《九章算术》是中国传统数学重要的著作之一,奠定了中国传统数学的基本框架.其中卷九中记载了一个问题:“今有圆材,埋在壁中,不知大小,以锯锯之,深一寸,锯道长一尺,问径几何?”其意思是:如图,AB为⊙O的直径,弦CD⊥AB于点E,BE=1寸,CD=1尺,那么直径AB的长为多少寸?(注:1尺=10寸)根据题意,该圆的直径为_____寸.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点E是正方形ABCD内一动点,满足∠AEB=90°且∠BAE<45°,过点D作DF⊥BE交BE的延长线于点F.
(1)依题意补全图形;
(2)用等式表示线段EF,DF,BE之间的数量关系,并证明;
(3)连接CE,若AB=2![]() ,请直接写出线段CE长度的最小值.
,请直接写出线段CE长度的最小值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,线段AB=5cm,∠BAM=90°,P是![]() 与∠BAM所围成的图形的外部的一定点,C是
与∠BAM所围成的图形的外部的一定点,C是![]() 上一动点,连接PC交弦AB于点D.设A,D两点间的距离为xcm,P,D两点间的距离为y1cm,P,C两点间的距离为y2cm.小腾根据学习函数的经验,分别对函数y1,y2随自变量x的变化而变化的规律进行了探究.
上一动点,连接PC交弦AB于点D.设A,D两点间的距离为xcm,P,D两点间的距离为y1cm,P,C两点间的距离为y2cm.小腾根据学习函数的经验,分别对函数y1,y2随自变量x的变化而变化的规律进行了探究.
下面是小腾的探究过程,请补充完整:
按照表中自变量x的值进行取点、画图、测量,分别得到了y1,y2与x的几组对应值:
x/cm | 0.00 | 1.00 | 1.56 | 1.98 | 2.50 | 3.38 | 4.00 | 4.40 | 5.00 |
y1/cm | 2.75 | 3.24 | 3.61 | 3.92 | 4.32 | 5.06 | 5.60 | 5.95 | 6.50 |
y2/cm | 2.75 | 4.74 | 5.34 | 5.66 | 5.94 | 6.24 | 6.37 | 6.43 | 6.50 |
(1)在同一平面直角坐标系xOy中,画出各组数值所对应的点(x,y1),(x,y2),并画出函数y1,y2的图象;
(2)连接BP,结合函数图象,解决问题:当△BDP为等腰三角形时,x的值约为_____cm(结果保留一位小数).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:点P为图形M上任意一点,点Q为图形N上任意一点,若点P与点Q之间的距离PQ始终满足PQ>0,则称图形M与图形N相离.
(1)已知点A(1,2)、B(0,﹣5)、C(2,﹣1)、D(3,4).
①与直线y=3x﹣5相离的点是 ;
②若直线y=3x+b与△ABC相离,求b的取值范围;
(2)设直线y=![]() x+3、直线y=﹣
x+3、直线y=﹣![]() x+3及直线y=﹣2围成的图形为W,⊙T的半径为1,圆心T的坐标为(t,0),直接写出⊙T与图形W相离的t的取值范围.
x+3及直线y=﹣2围成的图形为W,⊙T的半径为1,圆心T的坐标为(t,0),直接写出⊙T与图形W相离的t的取值范围.
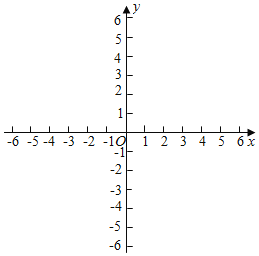
查看答案和解析>>
科目:初中数学 来源: 题型:
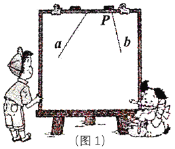
【题目】已知:如图1,直线![]() ,
,![]() 所成的角跑到画板外面去了,你有什么办法作出这两条直线所成角的角平分线?
所成的角跑到画板外面去了,你有什么办法作出这两条直线所成角的角平分线?
小明的做法是:
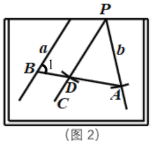
(1)如图2,画![]() ;
;
(2)以![]() 为圆心,任意长为半径画圆弧,分别交直线
为圆心,任意长为半径画圆弧,分别交直线![]() ,
,![]() 于点
于点![]() ,
,![]() ;
;
(3)连结![]() 并延长交直线
并延长交直线![]() 于点
于点![]() ;
;
请你先完成下面的证明,然后完成第(4)步作图:
∵![]()
∴![]() ( )
( )
∵以![]() 为圆心,任意长为半径画圆弧,分别交直线
为圆心,任意长为半径画圆弧,分别交直线![]() ,
,![]() 于点
于点![]() ,
,![]()
∴![]()
∴![]()
∴![]()
∴以直线![]() ,
,![]() 的交点和点
的交点和点![]() 、
、![]() 为顶点所构成的三角形为等腰三角形( )
为顶点所构成的三角形为等腰三角形( )
根据上面的推理证明完成第(4)步作图
(4)请在图2画板内作出“直线![]() ,
,![]() 所成的跑到画板外面去的角”的平分线(画板内的部分),尺规作出图形,并保留作图痕迹.
所成的跑到画板外面去的角”的平分线(画板内的部分),尺规作出图形,并保留作图痕迹.
第(4)步这么作图的理论依据是: .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com