
【题目】已知:在平面直角坐标系![]() 中,对于任意的实数
中,对于任意的实数![]() ,直线
,直线![]() 都经过平面内一个定点
都经过平面内一个定点![]() .
.
(1)求点![]() 的坐标.
的坐标.
(2)反比例函数![]() 的图象与直线
的图象与直线![]() 交于点
交于点![]() 和另外一点
和另外一点![]()
①求![]() 的值;
的值;
②当![]() 时,求
时,求![]() 的取值范围
的取值范围
【答案】(1) A(-1,-2);(2)①b=2, m>0或m<-1.
【解析】
(1)解析式化为y=ax+a-2=a(x+1)-2,即可求得;
(2)①根据待定系数法即可求得;②根据反比例函数的性质即可判定点P(m,n)在第一象限或第三象限两种情况,分别讨论即可.
解:(1)∵y=ax+a-2=a(x+1)-2,
∴当x=-1时,y=-2,
∴直线y=ax+a-2都经过平面内一个定点A(-1,-2);
故答案为:A(-1,-2).
(2)①∵反比例函数![]() 的图像经过点A,
的图像经过点A,
∴b=-1×(-2)=2;
②若点P(m,n)在第一象限,当n>-2时,m>0,
若点P(m,n)在第三象限,当n>-2时,m<-1,
综上,当n>-2时,m>0或m<-1.
故答案为:b=2,m的取值范围是:m>0或m<-1.


科目:初中数学 来源: 题型:
【题目】全球已经进入大数据时代,大数据(![]() )是指数据规模巨大,类型多样且信息传播速度快的数据库体系.大数据在推动经济发展,改善公共服务等方面日益显示出巨大的价值为创建大数据应用示范城市,我市某机构针对市民最关心的四类生活信息进行了民意调查(被调查者每人限送一项),下面是根据调查结果绘制出不完整的两个统计图表:
)是指数据规模巨大,类型多样且信息传播速度快的数据库体系.大数据在推动经济发展,改善公共服务等方面日益显示出巨大的价值为创建大数据应用示范城市,我市某机构针对市民最关心的四类生活信息进行了民意调查(被调查者每人限送一项),下面是根据调查结果绘制出不完整的两个统计图表:
生活信息关注度条形统计图
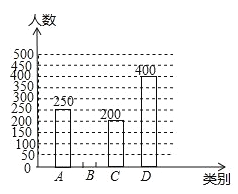
A:政府服务信息 B:城市医疗信息 C:交于资源信息 D:交通信息
生活信息关注度扇形统计图
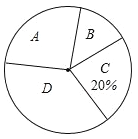
请根据图中提供的信息,解答下列问题:
(1)本次参与调查的人数是______,扇形统计图中![]() 部分的圆心角的度数是_______.并补全条形统计图;
部分的圆心角的度数是_______.并补全条形统计图;
(2)这次调查的市民最关心的四类生活信息的众数是_______类;
(3)若我市现有常住人口约600万,请你估计最关心“城市医疗信息”的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是小菲设计的“作一个角等于已知角的二倍”的尺规作图过程.
已知:![]() 中,
中,![]() .
.
求作:![]() ,使得
,使得![]() .
.
作法:如图,
①分别以点![]() 和点
和点![]() 为圆心,大于
为圆心,大于![]() 的长为半径作弧,两弧交于
的长为半径作弧,两弧交于![]() 、
、![]() 点,作直线
点,作直线![]() ;
;
②分别以点![]() 和点
和点![]() 为圆心,大于
为圆心,大于![]() 的长为半径作弧,两弧交于
的长为半径作弧,两弧交于![]() 、
、![]() 点,作直线
点,作直线![]() ,
,![]() 和
和![]() 交于点
交于点![]() ;
;
③连接![]() 和
和![]() ;
;
④以点![]() 为圆心,
为圆心,![]() 的长为半径作
的长为半径作![]() .
.
所以![]() .
.
根据小菲设计的尺规作图过程.
(1)使用直尺和圆规,补全图形(保留作图痕迹);

(2)完成下面的证明.

证明:连接![]()
∵![]() 和
和![]() 分别为
分别为![]() 、
、![]() 的垂直平分线,
的垂直平分线,
∴![]() ________.
________.
∴![]() 是
是![]() 的外接圆.
的外接圆.
∵点![]() 是
是![]() 上的一点,
上的一点,
∴![]() .(____________).(填推理的依据)
.(____________).(填推理的依据)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,存在抛物线
中,存在抛物线![]() 以及两点
以及两点![]() .
.
(1)求该抛物线的顶点坐标;(用含![]() 的代数式表示)
的代数式表示)
(2)若该抛物线经过点![]() ,求此抛物线的表达式;
,求此抛物线的表达式;
(3)若该抛物线与线段![]() 有公共点,结合图象,求
有公共点,结合图象,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A,B,C为平面内不在同一直线上的三点.点D为平面内一个动点.线段AB,BC,CD,DA的中点分别为M,N,P,Q.在点D的运动过程中,有下列结论:①存在无数个中点四边形MNPQ是平行四边形;②存在无数个中点四边形MNPQ是菱形;③存在无数个中点四边形MNPQ是矩形;④存在两个中点四边形MNPQ是正方形.所有正确结论的序号是_____.
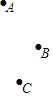
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A,B,C,D在⊙O上,弦AD的延长线与弦BC的延长线相交于点E.用①AB是⊙O的直径,②CB=CE,③AB=AE中的两个作为题设,余下的一个作为结论组成一个命题,则组成真命题的个数为( )
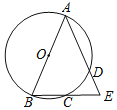
A.0B.1C.2D.3
查看答案和解析>>
科目:初中数学 来源: 题型:
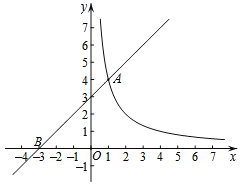
【题目】如图,在平面直角坐标系xOy中,直线y=x+3与函数y=![]() (x>0)的图象交于点A(1,m),与x轴交于点B.
(x>0)的图象交于点A(1,m),与x轴交于点B.
(1)求m,k的值;
(2)过动点P(0,n)(n>0)作平行于x轴的直线,交函数y=![]() (x>0)的图象于点C,交直线y=x+3于点D.
(x>0)的图象于点C,交直线y=x+3于点D.
①当n=2时,求线段CD的长;
②若CD≥OB,结合函数的图象,直接写出n的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
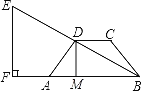
【题目】如图,在四边形ABCD中,AB∥DC,AD=BC,AB=10,CD=4,DM⊥AB于点M.连接BD并延长到E,使DE=BD,作EF⊥AB,交BA的延长线于点F.
(1)求MB的长;
(2)求AF的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com