
【题目】如图,在四边形ABCD中,AB∥DC,AD=BC,AB=10,CD=4,DM⊥AB于点M.连接BD并延长到E,使DE=BD,作EF⊥AB,交BA的延长线于点F.
(1)求MB的长;
(2)求AF的长.
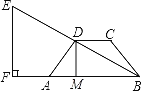
【答案】(1)MB=7;(2)AF=4.
【解析】
(1)作CN⊥AB于点N,然后即可证明四边形DMNC是矩形和△DMA≌△CNB,然后即可得到BM的长;
(2)根据(1)中的结果和三角形相似的知识,可以得到BF的长,然后根据AB=10,即可得到AF的长.
(1)作CN⊥AB于点N,
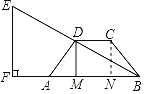
∵AB∥CD,DM⊥AB,CN⊥AB,
∴∠DMN=∠MNC=∠MDC=90°,
∴四边形DMNC是矩形,
∴DM=CN,DC=MN,
在Rt△DMA和Rt△CNB中,
![]() ,
,
∴Rt△DMA≌Rt△CNB(HL),
∴AM=BN,
∵AB=10,CD=4,
∴AM=BN=3,MN=4,
∴MB=MN+BN=7;
(2)∵DM⊥AB,EF⊥AB,
∴DM∥EF,
∴△BDM∽△BEF,
∴![]() ,
,
∵点D为BE的中点,
∴BD=![]() BE,
BE,
∴![]() =
=![]() ,
,
∴![]() =
=![]() ,
,
∵BM=7,
∴BF=14,
∵AB=10,
∴AF=BF﹣AB=14﹣10=4.


 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案科目:初中数学 来源: 题型:
【题目】在推进城乡生活垃圾分类的行动中,为了了解社区居民对垃圾分类知识的掌握情况,某社区随机抽取40名居民进行测试,并对他们的得分数据进行收集、整理、描述和分析.下面给出了部分信息:
a.社区40名居民得分的频数分布直方图:(数据分成5组:50≤x<60,60≤x<70,70≤x<80,80≤x<90,90≤x<100):
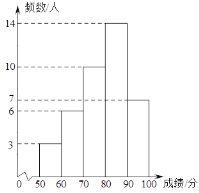
b.社区居民得分在80≤x<90这一组的是:
80 80 81 82 83 84 84 85 85 85 86 86 87 89
c.40个社区居民的年龄和垃圾分类知识得分情况统计图:
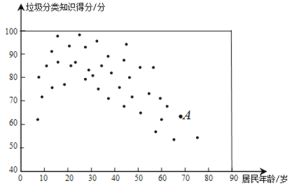
d.社区居民甲的垃圾分类知识得分为89分.
根据以上信息,回答下列问题:
(1)社区居民甲的得分在抽取的40名居民得分中从高到低排名第 ;
(2)在垃圾分类得分比居民甲得分高的居民中,居民年龄最大约是 岁;
(3)下列推断合理的是 .
①相比于点A所代表的社区居民,居民甲的得分略高一些,说明青年人比老年人垃圾分类知识掌握得更好一些;
②垃圾分类知识得分在90分以上的社区居民年龄主要集中在15岁到35岁之间,说明青年人垃圾分类知识掌握更为全面,他们可以向身边的老年人多宣传垃圾分类知识.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:在平面直角坐标系![]() 中,对于任意的实数
中,对于任意的实数![]() ,直线
,直线![]() 都经过平面内一个定点
都经过平面内一个定点![]() .
.
(1)求点![]() 的坐标.
的坐标.
(2)反比例函数![]() 的图象与直线
的图象与直线![]() 交于点
交于点![]() 和另外一点
和另外一点![]()
①求![]() 的值;
的值;
②当![]() 时,求
时,求![]() 的取值范围
的取值范围
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点E是正方形ABCD内一动点,满足∠AEB=90°且∠BAE<45°,过点D作DF⊥BE交BE的延长线于点F.
(1)依题意补全图形;
(2)用等式表示线段EF,DF,BE之间的数量关系,并证明;
(3)连接CE,若AB=2![]() ,请直接写出线段CE长度的最小值.
,请直接写出线段CE长度的最小值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,线段AB=5cm,∠BAM=90°,P是![]() 与∠BAM所围成的图形的外部的一定点,C是
与∠BAM所围成的图形的外部的一定点,C是![]() 上一动点,连接PC交弦AB于点D.设A,D两点间的距离为xcm,P,D两点间的距离为y1cm,P,C两点间的距离为y2cm.小腾根据学习函数的经验,分别对函数y1,y2随自变量x的变化而变化的规律进行了探究.
上一动点,连接PC交弦AB于点D.设A,D两点间的距离为xcm,P,D两点间的距离为y1cm,P,C两点间的距离为y2cm.小腾根据学习函数的经验,分别对函数y1,y2随自变量x的变化而变化的规律进行了探究.
下面是小腾的探究过程,请补充完整:
按照表中自变量x的值进行取点、画图、测量,分别得到了y1,y2与x的几组对应值:
x/cm | 0.00 | 1.00 | 1.56 | 1.98 | 2.50 | 3.38 | 4.00 | 4.40 | 5.00 |
y1/cm | 2.75 | 3.24 | 3.61 | 3.92 | 4.32 | 5.06 | 5.60 | 5.95 | 6.50 |
y2/cm | 2.75 | 4.74 | 5.34 | 5.66 | 5.94 | 6.24 | 6.37 | 6.43 | 6.50 |
(1)在同一平面直角坐标系xOy中,画出各组数值所对应的点(x,y1),(x,y2),并画出函数y1,y2的图象;
(2)连接BP,结合函数图象,解决问题:当△BDP为等腰三角形时,x的值约为_____cm(结果保留一位小数).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小宜跟几位同学在某快餐厅吃饭,如图为此快餐厅的菜单.若他们所点的餐食总共为10份盖饭,x杯饮料,y份凉拌菜.
(1)他们点了 份A套餐, 份B套餐, 份C套餐(均用含x或y的代数式表示);
(2)若x=6,且A、B、C套餐均至少点了1份,则最多有 种点餐方案.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:点P为图形M上任意一点,点Q为图形N上任意一点,若点P与点Q之间的距离PQ始终满足PQ>0,则称图形M与图形N相离.
(1)已知点A(1,2)、B(0,﹣5)、C(2,﹣1)、D(3,4).
①与直线y=3x﹣5相离的点是 ;
②若直线y=3x+b与△ABC相离,求b的取值范围;
(2)设直线y=![]() x+3、直线y=﹣
x+3、直线y=﹣![]() x+3及直线y=﹣2围成的图形为W,⊙T的半径为1,圆心T的坐标为(t,0),直接写出⊙T与图形W相离的t的取值范围.
x+3及直线y=﹣2围成的图形为W,⊙T的半径为1,圆心T的坐标为(t,0),直接写出⊙T与图形W相离的t的取值范围.
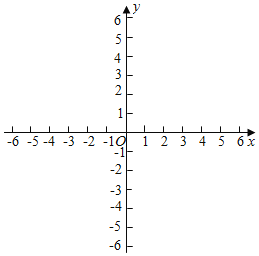
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图①是由五个完全相同的小正方体组成的立体图形.将图①中的一个小正方体改变位置后如图②,则三视图发生改变的是( )

A.主视图B.俯视图
C.左视图D.主视图、俯视图和左视图都改变
查看答案和解析>>
科目:初中数学 来源: 题型:
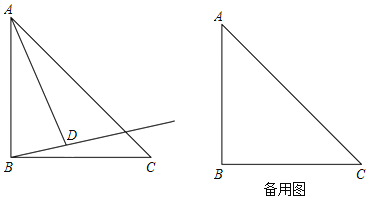
【题目】△ABC中,AB=BC,∠ABC=90°,将线段AB绕点A逆时针旋转α(0°<α<90°)得到线段AD.作射线BD,点C关于射线BD的对称点为点E.连接AE,CE.
(1)依题意补全图形;
(2)若α=20°,直接写出∠AEC的度数;
(3)写出一个α的值,使AE=![]() 时,线段CE的长为
时,线段CE的长为![]() ﹣1,并证明.
﹣1,并证明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com