
【题目】已知:如图,线段AB=5cm,∠BAM=90°,P是![]() 与∠BAM所围成的图形的外部的一定点,C是
与∠BAM所围成的图形的外部的一定点,C是![]() 上一动点,连接PC交弦AB于点D.设A,D两点间的距离为xcm,P,D两点间的距离为y1cm,P,C两点间的距离为y2cm.小腾根据学习函数的经验,分别对函数y1,y2随自变量x的变化而变化的规律进行了探究.
上一动点,连接PC交弦AB于点D.设A,D两点间的距离为xcm,P,D两点间的距离为y1cm,P,C两点间的距离为y2cm.小腾根据学习函数的经验,分别对函数y1,y2随自变量x的变化而变化的规律进行了探究.
下面是小腾的探究过程,请补充完整:
按照表中自变量x的值进行取点、画图、测量,分别得到了y1,y2与x的几组对应值:
x/cm | 0.00 | 1.00 | 1.56 | 1.98 | 2.50 | 3.38 | 4.00 | 4.40 | 5.00 |
y1/cm | 2.75 | 3.24 | 3.61 | 3.92 | 4.32 | 5.06 | 5.60 | 5.95 | 6.50 |
y2/cm | 2.75 | 4.74 | 5.34 | 5.66 | 5.94 | 6.24 | 6.37 | 6.43 | 6.50 |
(1)在同一平面直角坐标系xOy中,画出各组数值所对应的点(x,y1),(x,y2),并画出函数y1,y2的图象;
(2)连接BP,结合函数图象,解决问题:当△BDP为等腰三角形时,x的值约为_____cm(结果保留一位小数).

 星级口算天天练系列答案
星级口算天天练系列答案科目:初中数学 来源: 题型:
【题目】在△ABC中,CD是△ABC的中线,如果![]() 上的所有点都在△ABC的内部或边上,则称
上的所有点都在△ABC的内部或边上,则称![]() 为△ABC的中线弧.
为△ABC的中线弧.
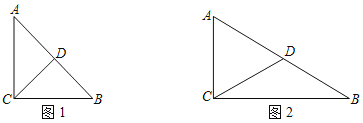
(1)在Rt△ABC中,∠ACB=90°,AC=1,D是AB的中点.
①如图1,若∠A=45°,画出△ABC的一条中线弧![]() ,直接写出△ABC的中线弧
,直接写出△ABC的中线弧![]() 所在圆的半径r的最小值;
所在圆的半径r的最小值;
②如图2,若∠A=60°,求出△ABC的最长的中线弧![]() 的弧长l.
的弧长l.
(2)在平面直角坐标系中,已知点A(2,2),B(4,0),C(0,0),在△ABC中,D是AB的中点.求△ABC的中线弧![]() 所在圆的圆心P的纵坐标t的取值范围.
所在圆的圆心P的纵坐标t的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A,B,C为平面内不在同一直线上的三点.点D为平面内一个动点.线段AB,BC,CD,DA的中点分别为M,N,P,Q.在点D的运动过程中,有下列结论:①存在无数个中点四边形MNPQ是平行四边形;②存在无数个中点四边形MNPQ是菱形;③存在无数个中点四边形MNPQ是矩形;④存在两个中点四边形MNPQ是正方形.所有正确结论的序号是_____.
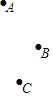
查看答案和解析>>
科目:初中数学 来源: 题型:
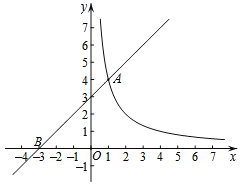
【题目】如图,在平面直角坐标系xOy中,直线y=x+3与函数y=![]() (x>0)的图象交于点A(1,m),与x轴交于点B.
(x>0)的图象交于点A(1,m),与x轴交于点B.
(1)求m,k的值;
(2)过动点P(0,n)(n>0)作平行于x轴的直线,交函数y=![]() (x>0)的图象于点C,交直线y=x+3于点D.
(x>0)的图象于点C,交直线y=x+3于点D.
①当n=2时,求线段CD的长;
②若CD≥OB,结合函数的图象,直接写出n的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】众志成城,抗击疫情,救助重灾区.某校某小组7名同学积极捐出自己的零花钱支援灾区,他们捐款的数额分别是(单位:元):100,45,100,40,100,60,155.下面有四个推断:
①这7名同学所捐的零花钱的平均数是150;
②这7名同学所捐的零花钱的中位数是100;
③这7名同学所捐的零花钱的众数是100;
④由这7名同学所捐的零花钱的中位数是100,可以推断该校全体同学所捐的零花钱的中位数也一定是100.
所有合理推断的序号是( )
A.①③B.②③C.②④D.②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
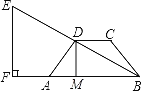
【题目】如图,在四边形ABCD中,AB∥DC,AD=BC,AB=10,CD=4,DM⊥AB于点M.连接BD并延长到E,使DE=BD,作EF⊥AB,交BA的延长线于点F.
(1)求MB的长;
(2)求AF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2019年11月,胡润研究院携手知识产权与科创云平台汇桔,联合发布《IP助燃AI新纪元﹣2019中国人工智能产业知识产权发展白皮书》,白皮书公布了2019中国人工智能企业知识产权竞争力百强榜,对500余家中国人工智能主流企业进行定量评估(满分100分),前三名分别为:华为、腾讯、百度.对得分由高到低的前41家企业的有关数据进行收集、整理、描述和分析.下面给出了部分信息:
a.得分的频数分布直方图:
(数据分成8组:60≤x<65,65≤x<70,70≤x<75,75≤x<80,80≤x<85,85≤x<90,90≤x<95,95≤x≤100,)
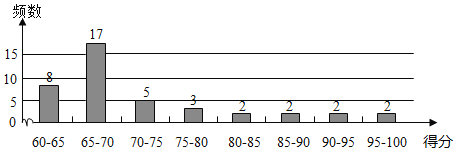
b.知识产权竞争力得分在70≤x<75这一组的是:70.3,71.6,72.1,72.5,74.1.
c.41家企业注册所在城市分布图(不完整)如图:(结果保留一位小数)
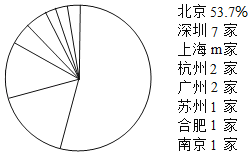
d.汉王科技股份有限公司的知识产权竞争力得分是70.3.
(以上数据来源于《IP助燃AI新纪元﹣2019中国人工智能产业知识产权发展白皮书》)
根据以上信息,回答下列问题:
(1)汉王科技股份有限公司的知识产权竞争力得分排名是第 ;
(2)百度在人工智能领域取得诸多成果,尤其在智能家居、自动驾驶与服务于企业的智能云领域,百度都已进行前瞻布局,请你估计百度在本次排行榜中的得分大概是 ;
(3)在41家企业注册所在城市分布图中,m= ,请用阴影标出代表上海的区域;
(4)下列推断合理的是 .(只填序号)
①前41家企业的知识产权竞争力得分的中位数应在65≤x<70这一组中,众数在65≤x<70这一组的可能性最大;
②前41家企业分布于我国8个城市.人工智能产业的发展聚集于经济、科技、教育相对发达的城市,一线城市中,北京的优势尤其突出,贡献榜单过半的企业,充分体现北京在人工智能领域的产业集群优势.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2020年,由于“疫情”的原因,学校未能准时开学,某中学为了了解学生在家“课间”活动情况,在七、八、九年级的学生中,分别抽取了相同数量的学生对“你最喜欢的运动项目”在线进行调查(每人只能选一项),调查结果的部分数据如下表(图)所示,其中七年级最喜欢跳绳的人数比八年级多5人,九年级最喜欢排球的人数为10人.
七年级学生最喜欢的运动项目人数统计表
项目 | 排球 | 篮球 | 踢毽 | 跳绳 | 其他 |
人数(人) | 7 | 8 | 14 | 6 |
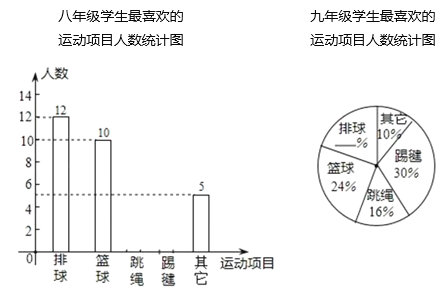
请根据以上统计表(图)解答下列问题:
(1)本次调查共抽取的人数为 人;
(2)请直接补全统计表和统计图;
(3)根据抽样调查的结果,请你估计该校1500名学生中有多少名学生最喜欢踢毽子?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等边△ABC,作它的外接圆⊙O,连接AO并延长交⊙O于点D,交BC于点E,过点D作DF∥BC,交AC的延长线于点F.
(1)依题意补全图形并证明:DF与⊙O相切;
(2)若AB=6,求CF的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com