
【题目】如图,点A,B,C为平面内不在同一直线上的三点.点D为平面内一个动点.线段AB,BC,CD,DA的中点分别为M,N,P,Q.在点D的运动过程中,有下列结论:①存在无数个中点四边形MNPQ是平行四边形;②存在无数个中点四边形MNPQ是菱形;③存在无数个中点四边形MNPQ是矩形;④存在两个中点四边形MNPQ是正方形.所有正确结论的序号是_____.
【答案】①②③④.
【解析】
连接AC、BD,根据三角形中位线定理得到PQ∥AC,PQ=![]() AC,MN∥AC,MN=
AC,MN∥AC,MN=![]() AC,根据平行四边形、矩形、菱形、正方形的判定定理判断即可.
AC,根据平行四边形、矩形、菱形、正方形的判定定理判断即可.
①当AC与BD不平行时,中点四边形MNPQ是平行四边形;
故存在无数个中点四边形MNPQ是平行四边形;
②当AC与BD相等且不平行时,中点四边形MNPQ是菱形;
故存在无数个中点四边形MNPQ是菱形;
③当AC与BD互相垂直(B,D不重合)时,中点四边形MNPQ是矩形;
故存在无数个中点四边形MNPQ是矩形;
④如图所示,当AC与BD相等且互相垂直时,中点四边形MNPQ是正方形.
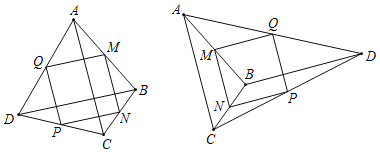
故存在两个中点四边形MNPQ是正方形.
故答案为:①②③④.


 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案科目:初中数学 来源: 题型:
【题目】某校在开展读书交流活动中,全体师生积极捐书,为了解所捐书籍的种类,对部分书籍进行了抽样调查,张老师根据调查数据绘制了如下不完整的统计图.
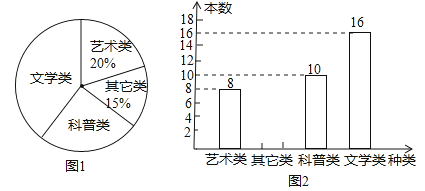
请根据统计图回答下列问题:
(1)本次抽样调查的书籍有多少本?
(2)试求图1中表示文学类书籍的扇形圆心角的度数,并补全条形统计图.
(3)本次活动师生共捐书![]() 本,请估计有多少本科普类书籍?
本,请估计有多少本科普类书籍?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于平面直角坐标系xOy中的任意点![]() ,如果满足
,如果满足![]() (x≥0,a为常数),那么我们称这样的点叫做“特征点”.
(x≥0,a为常数),那么我们称这样的点叫做“特征点”.
(1)当2≤a≤3时,
①在点![]() 中,满足此条件的特征点为__________________;
中,满足此条件的特征点为__________________;
②⊙W的圆心为![]() ,半径为1,如果⊙W上始终存在满足条件的特征点,请画出示意图,并直接写出m的取值范围;
,半径为1,如果⊙W上始终存在满足条件的特征点,请画出示意图,并直接写出m的取值范围;
(2)已知函数![]() ,请利用特征点求出该函数的最小值.
,请利用特征点求出该函数的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果![]() 的两个端点
的两个端点![]() 分别在
分别在![]() 的两边上(不与点
的两边上(不与点![]() 重合),并且
重合),并且![]() 除端点外的所有点都在
除端点外的所有点都在![]() 的内部,则称
的内部,则称![]() 是
是![]() 的“连角弧”.
的“连角弧”.
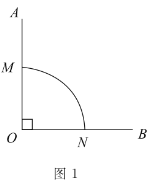
(1)图1中,![]() 是直角,
是直角,![]() 是以
是以![]() 为圆心,半径为1的“连角弧”.
为圆心,半径为1的“连角弧”.
①图中![]() 的长是______,并在图中再作一条以
的长是______,并在图中再作一条以![]() 为端点、长度相同的“连角弧”;
为端点、长度相同的“连角弧”;
②以![]() 为端点,弧长最长的“连角弧”的长度是_______.
为端点,弧长最长的“连角弧”的长度是_______.
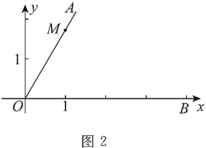
(2)如图2,在平面直角坐标系![]() 中,点
中,点![]() ,点
,点![]() 在
在![]() 轴正半轴上,若
轴正半轴上,若![]() 是半圆,也是
是半圆,也是![]() 的“连角弧”,求
的“连角弧”,求![]() 的取值范围.
的取值范围.
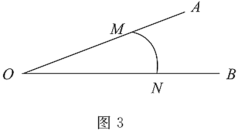
(3)如图3,已知点![]() 分别在射线
分别在射线![]() 上,
上,![]() 是
是![]() 的“连角弧”,且
的“连角弧”,且![]() 所在圆的半径为
所在圆的半径为![]() ,直接写出
,直接写出![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:在平面直角坐标系![]() 中,对于任意的实数
中,对于任意的实数![]() ,直线
,直线![]() 都经过平面内一个定点
都经过平面内一个定点![]() .
.
(1)求点![]() 的坐标.
的坐标.
(2)反比例函数![]() 的图象与直线
的图象与直线![]() 交于点
交于点![]() 和另外一点
和另外一点![]()
①求![]() 的值;
的值;
②当![]() 时,求
时,求![]() 的取值范围
的取值范围
查看答案和解析>>
科目:初中数学 来源: 题型:
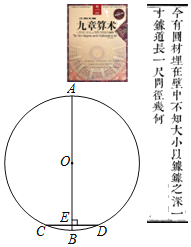
【题目】《九章算术》是中国传统数学重要的著作之一,奠定了中国传统数学的基本框架.其中卷九中记载了一个问题:“今有圆材,埋在壁中,不知大小,以锯锯之,深一寸,锯道长一尺,问径几何?”其意思是:如图,AB为⊙O的直径,弦CD⊥AB于点E,BE=1寸,CD=1尺,那么直径AB的长为多少寸?(注:1尺=10寸)根据题意,该圆的直径为_____寸.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,线段AB=5cm,∠BAM=90°,P是![]() 与∠BAM所围成的图形的外部的一定点,C是
与∠BAM所围成的图形的外部的一定点,C是![]() 上一动点,连接PC交弦AB于点D.设A,D两点间的距离为xcm,P,D两点间的距离为y1cm,P,C两点间的距离为y2cm.小腾根据学习函数的经验,分别对函数y1,y2随自变量x的变化而变化的规律进行了探究.
上一动点,连接PC交弦AB于点D.设A,D两点间的距离为xcm,P,D两点间的距离为y1cm,P,C两点间的距离为y2cm.小腾根据学习函数的经验,分别对函数y1,y2随自变量x的变化而变化的规律进行了探究.
下面是小腾的探究过程,请补充完整:
按照表中自变量x的值进行取点、画图、测量,分别得到了y1,y2与x的几组对应值:
x/cm | 0.00 | 1.00 | 1.56 | 1.98 | 2.50 | 3.38 | 4.00 | 4.40 | 5.00 |
y1/cm | 2.75 | 3.24 | 3.61 | 3.92 | 4.32 | 5.06 | 5.60 | 5.95 | 6.50 |
y2/cm | 2.75 | 4.74 | 5.34 | 5.66 | 5.94 | 6.24 | 6.37 | 6.43 | 6.50 |
(1)在同一平面直角坐标系xOy中,画出各组数值所对应的点(x,y1),(x,y2),并画出函数y1,y2的图象;
(2)连接BP,结合函数图象,解决问题:当△BDP为等腰三角形时,x的值约为_____cm(结果保留一位小数).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知二次函数y=﹣x2+bx+c的图象经过点A(3,1),点B(0,4).
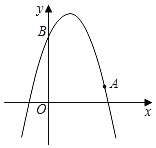
(1)求该二次函数的表达式及顶点坐标;
(2)点C(m,n)在该二次函数图象上.
①当m=﹣1时,求n的值;
②当m≤x≤3时,n最大值为5,最小值为1,请根据图象直接写出m的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com