练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

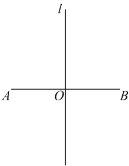
    【题目】已知线段，直线垂直平分且交于点．以为圆心，长为半径作弧，交直线于两点，分别连接．

    (1)根据题意，补全图形；

    (2)求证：四边形为正方形．

    【答案】(1)见解析；(2)证明过程见解析.

    【解析】

    （1）直接根据题意中垂直平分线的尺规作图画出图形即可；

    （2）直接利用基本作图方法结合正方形的判定方法得出答案．

    解：（1）如下图所示：

    （2）证明：∵直线l垂直平分AB，

    ∴AC=BC，BD=AD，∠AOC=∠AOD=90°，且CO与DO都是以O为圆心的半径，

    在△AOC和△AOD中

    ∴△AOC≌△AOD（SAS），

    ∴AC=BC=BD=AD，

    ∴四边形ACBD是菱形，

    又∵OA=OB=OC=OD，

    ∴∠CAD=45°+45°=90°，

    ∴菱形ACBD为正方形．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

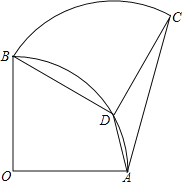
    【题目】如图，扇形OAB中，∠AOB＝90°，将扇形OAB绕点B逆时针旋转，得到扇形BDC，若点O刚好落在弧AB上的点D处，则的值为（　　）

    A.B.C.D.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在△ABC中，CD是△ABC的中线，如果上的所有点都在△ABC的内部或边上，则称为△ABC的中线弧．

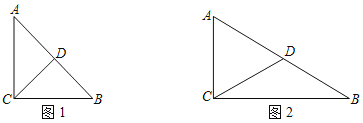
    （1）在Rt△ABC中，∠ACB＝90°，AC＝1，D是AB的中点．

    ①如图1，若∠A＝45°，画出△ABC的一条中线弧，直接写出△ABC的中线弧所在圆的半径r的最小值；

    ②如图2，若∠A＝60°，求出△ABC的最长的中线弧的弧长l．

    （2）在平面直角坐标系中，已知点A（2，2），B（4，0），C（0，0），在△ABC中，D是AB的中点．求△ABC的中线弧所在圆的圆心P的纵坐标t的取值范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】下面是小菲设计的“作一个角等于已知角的二倍”的尺规作图过程．

    已知：中，．

    求作：，使得．

    作法：如图，

    ①分别以点和点为圆心，大于的长为半径作弧，两弧交于、点，作直线；

    ②分别以点和点为圆心，大于的长为半径作弧，两弧交于、点，作直线，和交于点；

    ③连接和；

    ④以点为圆心，的长为半径作．

    所以．

    根据小菲设计的尺规作图过程．

    （1）使用直尺和圆规，补全图形（保留作图痕迹）；

    （2）完成下面的证明．

    证明：连接

    ∵和分别为、的垂直平分线，

    ∴________．

    ∴是的外接圆．

    ∵点是上的一点，

    ∴．（____________）．（填推理的依据）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】改革开放以来，人们的支付方式发生了巨大转变，近年来，移动支付已成为主要的支付方式之一，为了解某校学生上个月两种移动支付方式的使用情况，从全校名学生中随机抽取了人，发现样本中两种支付方式都不使用的有人，样本中仅使用种支付方式和仅使用种支付方式的学生的支付金额(元)的分布情况如下：

    支付金额（元）

    支付方式

    仅使用

    人

    人

    人

    仅使用

    人

    人

    人

    下面有四个推断：

    ①从样本中使用移动支付的学生中随机抽取一名学生，该生使用A支付方式的概率大于他使用B支付方式的概率；

    ②根据样本数据估计，全校1000名学生中．同时使用A、B两种支付方式的大约有400人；

    ③样本中仅使用A种支付方式的同学，上个月的支付金额的中位数一定不超过1000元；

    ④样本中仅使用B种支付方式的同学，上个月的支付金额的平均数一定不低于1000元．其中合理的是（ ）

    A.①③B.②④C.①②③D.①②③④

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在平面直角坐标系中，存在抛物线以及两点．

    (1)求该抛物线的顶点坐标；(用含的代数式表示)

    (2)若该抛物线经过点，求此抛物线的表达式；

    (3)若该抛物线与线段有公共点，结合图象，求的取值范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，点A，B，C为平面内不在同一直线上的三点．点D为平面内一个动点．线段AB，BC，CD，DA的中点分别为M，N，P，Q．在点D的运动过程中，有下列结论：①存在无数个中点四边形MNPQ是平行四边形；②存在无数个中点四边形MNPQ是菱形；③存在无数个中点四边形MNPQ是矩形；④存在两个中点四边形MNPQ是正方形．所有正确结论的序号是_____．

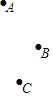
    查看答案和解析>>

    科目：初中数学 来源： 题型：

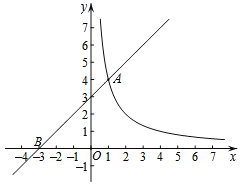
    【题目】如图，在平面直角坐标系xOy中，直线y＝x+3与函数y＝（x＞0）的图象交于点A（1，m），与x轴交于点B．

    （1）求m，k的值；

    （2）过动点P（0，n）（n＞0）作平行于x轴的直线，交函数y＝（x＞0）的图象于点C，交直线y＝x+3于点D．

    ①当n＝2时，求线段CD的长；

    ②若CD≥OB，结合函数的图象，直接写出n的取值范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】2020年，由于“疫情”的原因，学校未能准时开学，某中学为了了解学生在家“课间”活动情况，在七、八、九年级的学生中，分别抽取了相同数量的学生对“你最喜欢的运动项目”在线进行调查（每人只能选一项），调查结果的部分数据如下表（图）所示，其中七年级最喜欢跳绳的人数比八年级多5人，九年级最喜欢排球的人数为10人．

    七年级学生最喜欢的运动项目人数统计表

    项目

    排球

    篮球

    踢毽

    跳绳

    其他

    人数（人）

    7

    8

    14

    6

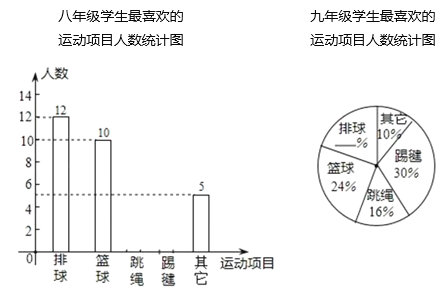
    请根据以上统计表（图）解答下列问题：

    （1）本次调查共抽取的人数为 人；

    （2）请直接补全统计表和统计图；

    （3）根据抽样调查的结果，请你估计该校1500名学生中有多少名学生最喜欢踢毽子？

    查看答案和解析>>

    同步练习册答案