练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】改革开放以来，人们的支付方式发生了巨大转变，近年来，移动支付已成为主要的支付方式之一，为了解某校学生上个月两种移动支付方式的使用情况，从全校名学生中随机抽取了人，发现样本中两种支付方式都不使用的有人，样本中仅使用种支付方式和仅使用种支付方式的学生的支付金额(元)的分布情况如下：

    支付金额（元）

    支付方式

    仅使用

    人

    人

    人

    仅使用

    人

    人

    人

    下面有四个推断：

    ①从样本中使用移动支付的学生中随机抽取一名学生，该生使用A支付方式的概率大于他使用B支付方式的概率；

    ②根据样本数据估计，全校1000名学生中．同时使用A、B两种支付方式的大约有400人；

    ③样本中仅使用A种支付方式的同学，上个月的支付金额的中位数一定不超过1000元；

    ④样本中仅使用B种支付方式的同学，上个月的支付金额的平均数一定不低于1000元．其中合理的是（ ）

    A.①③B.②④C.①②③D.①②③④

    【答案】C

    【解析】

    由题意根据概率公式、样本估计总体思想的运用、中位数和平均数的定义逐一判断可得．

    解：①从样本中使用移动支付的学生中随机抽取一名学生，该生使用A支付方式的概率为

    ，使用B支付方式的概率为，此推断合理；

    ②根据样本数据估计，全校1000名学生中，同时使用A，B两种支付方式的大约有（人），此推断合理；

    ③样本中仅使用A种支付方式的同学，第15、16个数据均落在0＜a≤1000，所以上个月的支付金额的中位数一定不超过1000元，此推断合理；

    ④样本中仅使用B种支付方式的同学，上个月的支付金额的平均数无法估计，此推断不正确．

    故推断正确的有①②③.

    故选：C．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】已知抛物线y=ax2+bx+a+2(a≠0)与x轴交于点A(x1，0)，点B(x2，0)，(点A在点B的左侧)，抛物线的对称轴为直线x=-1．

    (1)若点A的坐标为(-3，0)，求抛物线的表达式及点B的坐标；

    (2)C是第三象限的点，且点C的横坐标为-2，若抛物线恰好经过点C，直接写出x2的取值范围；

    (3)抛物线的对称轴与x轴交于点D，点P在抛物线上，且∠DOP=45°，若抛物线上满足条件的点P恰有4个，结合图象，求a的取值范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，直线l与⊙O相离，OA⊥l于点A，与⊙O相交于点P，OA＝5．C是直线l上一点，连接CP并延长，交⊙O于点B，且AB＝AC．

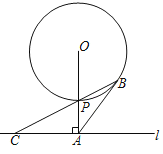
    （1）求证：AB是⊙O的切线；

    （2）若tan∠ACB＝，求线段BP的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】对于平面直角坐标系xOy中的任意点，如果满足 (x≥0，a为常数)，那么我们称这样的点叫做“特征点”．

    （1）当2≤a≤3时，

    ①在点中，满足此条件的特征点为__________________；

    ②⊙W的圆心为，半径为1，如果⊙W上始终存在满足条件的特征点，请画出示意图，并直接写出m的取值范围；

    （2）已知函数，请利用特征点求出该函数的最小值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】2020年新冠肺炎疫情发生以来，我市广大在职党员积极参与社区防疫工作，助力社区坚决打赢疫情防控阻击战．其中，社区有500名在职党员，为了解本社区2月-3月期间在职党员参加应急执勤的情况，社区针对执勤的次数随机抽取50名在职党员进行调查，并对数据进行了整理、描述和分析，下面给出了部分信息．

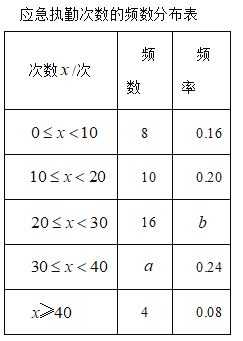
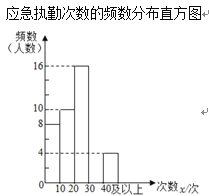
    其中，应急执勤次数在这一组的数据是：

    20 20 21 22 23 23 23 23 25 26 26 26 27 28 28 29

    请根据所给信息，解答下列问题：

    （1）______，______；

    （2）请补全频数分布直方图；

    （3）随机抽取的50名在职党员参加应急执勤次数的中位数是______；

    （4）请估计2月-3月期间社区在职党员参加应急执勤的次数不低于30次的约有______人．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知线段，直线垂直平分且交于点．以为圆心，长为半径作弧，交直线于两点，分别连接．

    (1)根据题意，补全图形；

    (2)求证：四边形为正方形．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如果的两个端点分别在的两边上(不与点重合)，并且除端点外的所有点都在的内部，则称是的“连角弧”．

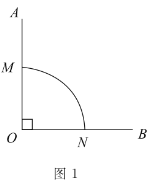
    (1)图1中，是直角，是以为圆心，半径为1的“连角弧”．

    ①图中的长是______，并在图中再作一条以为端点、长度相同的“连角弧”；

    ②以为端点，弧长最长的“连角弧”的长度是_______．

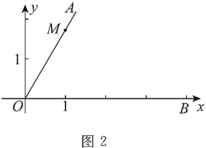
    (2)如图2，在平面直角坐标系中，点，点在轴正半轴上，若是半圆，也是的“连角弧”，求的取值范围．

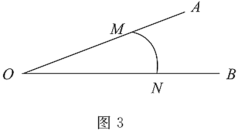
    (3)如图3，已知点分别在射线上，是的“连角弧”，且所在圆的半径为，直接写出的取值范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

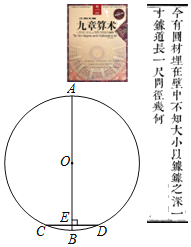
    【题目】《九章算术》是中国传统数学重要的著作之一，奠定了中国传统数学的基本框架．其中卷九中记载了一个问题：“今有圆材，埋在壁中，不知大小，以锯锯之，深一寸，锯道长一尺，问径几何？”其意思是：如图，AB为⊙O的直径，弦CD⊥AB于点E，BE＝1寸，CD＝1尺，那么直径AB的长为多少寸？（注：1尺＝10寸）根据题意，该圆的直径为_____寸．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某校举办球赛，分为若干组，其中第一组有A，B，C，D，E五个队．这五个队要进行单循环赛，即每两个队之间要进行一场比赛，每场比赛采用三局两胜制，即三局中胜两局就获胜．每场比赛胜负双方根据比分会获得相应的积分，积分均为正整数．这五个队完成所有比赛后得到如下的积分表．

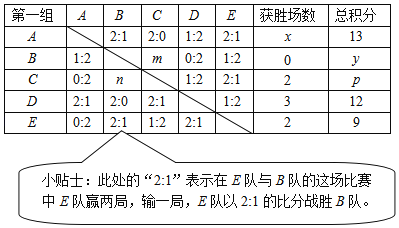
    根据上表回答下列问题：

    （1）第一组一共进行了　 　场比赛，A队的获胜场数x为　 　；

    （2）当B队的总积分y=6时，上表中m处应填　 　，n处应填　 　；

    （3）写出C队总积分p的所有可能值为：　 　．

    查看答案和解析>>

    同步练习册答案