
【题目】如图,直线l与⊙O相离,OA⊥l于点A,与⊙O相交于点P,OA=5.C是直线l上一点,连接CP并延长,交⊙O于点B,且AB=AC.
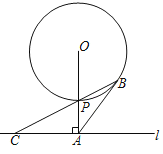
(1)求证:AB是⊙O的切线;
(2)若tan∠ACB=![]() ,求线段BP的长.
,求线段BP的长.
【答案】(1)详见解析;(2)![]()
【解析】
(1)连接OB,由等腰三角形的性质可得∠ACB=∠ABC,∠OBP=∠OPB=∠CPA,由余角的性质可求∠ABO=90°,可得结论;
(2)过点O作OD⊥BP于D,设AP=x,AC=2x,由勾股定理可求AP=2,AC=4,由勾股定理可求CP的长,通过证明△ACP∽△DOP,可求PD的长,由等腰三角形的性质可求BP的长.
证明:(1)连接OB,则OP=OB,

∴∠OBP=∠OPB=∠CPA,
∵AB=AC,
∴∠ACB=∠ABC,
∵OA⊥l,
∴∠OAC=90°,
∴∠ACB+∠CPA=90°,
∴∠ABP+∠OBP=90°,
∴∠ABO=90°,
∴OB⊥AB,
∴AB是⊙O的切线;
(2)如图,过点O作OD⊥BP于D,
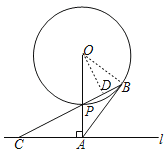
∵tan∠ACB=![]() ,
,
∴设AP=x,AC=2x,
∴AB=2x,OP=OB=5﹣x,
∵AO2=OB2+AB2,
∴25=(5﹣x)2+4x2,
∴x=2,
∴AP=2,AC=4
∴OB=OP=3,
∴CP=![]() ,
,
∵∠CAP=∠ODP=90°,∠APC=∠OPD,
∴△ACP∽△DOP,
∴![]() ,
,
∴PD=![]() ,
,
∵OB=OP,OD⊥BP,
∴BP=2PD=![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】五一前夕,某时装店老板到厂家选购![]() 两种品牌的时装,若购进
两种品牌的时装,若购进![]() 品牌的时装
品牌的时装![]() 套,
套,![]() 品牌的时装
品牌的时装![]() 套,需要
套,需要![]() 元;若购进
元;若购进![]() 品牌的时装
品牌的时装![]() 套,
套,![]() 品牌的时装
品牌的时装![]() 套,需要
套,需要![]() 元.
元.
(1)求![]() 两种品牌的时装每套进价分别为多少元?
两种品牌的时装每套进价分别为多少元?
(2)若![]() 套
套![]() 品牌的时装售价
品牌的时装售价![]() 元,
元,![]() 套
套![]() 品牌的时装售价
品牌的时装售价![]() 元,时装店将购进的
元,时装店将购进的![]() 两种时装共
两种时装共![]() 套全部售出,所获利润要不少于
套全部售出,所获利润要不少于![]() 元,问
元,问![]() 品牌时装至少购进多少套?
品牌时装至少购进多少套?
查看答案和解析>>
科目:初中数学 来源: 题型:
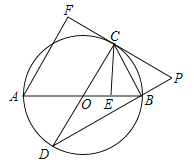
【题目】(2017广东省)如图,AB是⊙O的直径,AB=![]() ,点E为线段OB上一点(不与O,B重合),作CE⊥OB,交⊙O于点C,垂足为点E,作直径CD,过点C的切线交DB的延长线于点P,AF⊥PC于点F,连接CB.
,点E为线段OB上一点(不与O,B重合),作CE⊥OB,交⊙O于点C,垂足为点E,作直径CD,过点C的切线交DB的延长线于点P,AF⊥PC于点F,连接CB.
(1)求证:CB是∠ECP的平分线;
(2)求证:CF=CE;
(3)当![]() 时,求劣弧
时,求劣弧![]() 的长度(结果保留π)
的长度(结果保留π)
查看答案和解析>>
科目:初中数学 来源: 题型:
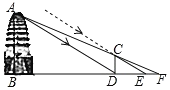
【题目】如图,西安市荐福寺内的小雁塔,是中国早期方形密檐式砖塔的典型作品,并作为丝绸之路的一处重要遗址点,被列入《世界遗产名录》.某周末,小乐和小夏相约去小雁塔游玩,在休息时,他们想利用所学知识测量小雁塔的高度,于是他们向工作人员借来测量工具由于观测点与小雁塔底部间的距离不易测量,于是他们利用太阳光照射影子进行测量,小乐先在小雁塔的影子顶端![]() 处竖直立一根长1.72米的木棒
处竖直立一根长1.72米的木棒![]() ,并测得此时木棒的影长
,并测得此时木棒的影长![]() 米;然后小夏在
米;然后小夏在![]() 的延长线上找出一点
的延长线上找出一点![]() ,使得
,使得![]() 、
、![]() 、
、![]() 三点在同一直线上,并测得
三点在同一直线上,并测得![]() 米已知图中所有点均在同一平面内,
米已知图中所有点均在同一平面内,![]() ,
,![]() ,根据以上测量过程及数据,请你帮他们求出小雁塔的高度
,根据以上测量过程及数据,请你帮他们求出小雁塔的高度![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
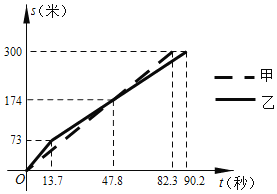
【题目】甲、乙两队参加了“端午情,龙舟韵”赛龙舟比赛,两队在比赛时的路程s(米)与时间t(秒)之间的函数图象如图所示,根据图象有以下四个判断:
①乙队率先到达终点;
②甲队比乙队多走了126米;
③在47.8秒时,两队所走路程相等;
④从出发到13.7秒的时间段内,甲队的速度比乙队的慢.
所有正确判断的序号是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,CD是△ABC的中线,如果![]() 上的所有点都在△ABC的内部或边上,则称
上的所有点都在△ABC的内部或边上,则称![]() 为△ABC的中线弧.
为△ABC的中线弧.
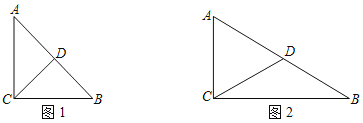
(1)在Rt△ABC中,∠ACB=90°,AC=1,D是AB的中点.
①如图1,若∠A=45°,画出△ABC的一条中线弧![]() ,直接写出△ABC的中线弧
,直接写出△ABC的中线弧![]() 所在圆的半径r的最小值;
所在圆的半径r的最小值;
②如图2,若∠A=60°,求出△ABC的最长的中线弧![]() 的弧长l.
的弧长l.
(2)在平面直角坐标系中,已知点A(2,2),B(4,0),C(0,0),在△ABC中,D是AB的中点.求△ABC的中线弧![]() 所在圆的圆心P的纵坐标t的取值范围.
所在圆的圆心P的纵坐标t的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】疫情期间,甲、乙、丙、丁4名同学约定周一至周五每天做一组俯卧撑.为了增加趣味性,他们通过游戏方式确定每个人每天的训练计划.
首先,按如图方式摆放五张卡片,正面标有不同的数字代表每天做俯卧撑的个数,反面标有![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 便于记录.
便于记录.
![]()
具体游戏规则如下:
甲同学:同时翻开![]() ,
,![]() ,将两个数字进行比较,然后由小到大记录在表格中,
,将两个数字进行比较,然后由小到大记录在表格中,![]() ,
,![]() ,
,![]() 按原顺序记录在表格中;
按原顺序记录在表格中;
乙同学:同时翻开![]() ,
,![]() ,
,![]() ,将三个数字进行比较,然后由小到大记录在表格中,
,将三个数字进行比较,然后由小到大记录在表格中,![]() ,
,![]() 按原顺序记录在表格中;
按原顺序记录在表格中;
以此类推,到丁同学时,五张卡片全部翻开,并由小到大记录在表格中.
下表记录的是这四名同学五天的训练计划:
星期一 | 星期二 | 星期三 | 星期四 | 星期五 | |
甲同学 |
|
|
|
|
|
乙同学 |
|
|
|
|
|
丙同学 | |||||
丁同学 |
|
|
|
|
|
根据记录结果解决问题:
(1)补全上表中丙同学的训练计划;
(2)已知每名同学每天至少做30个,五天最多做180个.
①如果![]() ,
,![]() ,那么
,那么![]() 所有可能取值为__________________________;
所有可能取值为__________________________;
②这四名同学星期_________做俯卧撑的总个数最多,总个数最多为_________个.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】改革开放以来,人们的支付方式发生了巨大转变,近年来,移动支付已成为主要的支付方式之一,为了解某校学生上个月![]() 两种移动支付方式的使用情况,从全校
两种移动支付方式的使用情况,从全校![]() 名学生中随机抽取了
名学生中随机抽取了![]() 人,发现样本中
人,发现样本中![]() 两种支付方式都不使用的有
两种支付方式都不使用的有![]() 人,样本中仅使用
人,样本中仅使用![]() 种支付方式和仅使用
种支付方式和仅使用![]() 种支付方式的学生的支付金额
种支付方式的学生的支付金额![]() (元)的分布情况如下:
(元)的分布情况如下:
支付金额 支付方式 |
|
|
|
仅使用 |
|
|
|
仅使用 |
|
|
|
下面有四个推断:
①从样本中使用移动支付的学生中随机抽取一名学生,该生使用A支付方式的概率大于他使用B支付方式的概率;
②根据样本数据估计,全校1000名学生中.同时使用A、B两种支付方式的大约有400人;
③样本中仅使用A种支付方式的同学,上个月的支付金额的中位数一定不超过1000元;
④样本中仅使用B种支付方式的同学,上个月的支付金额的平均数一定不低于1000元.其中合理的是( )
A.①③B.②④C.①②③D.①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】众志成城,抗击疫情,救助重灾区.某校某小组7名同学积极捐出自己的零花钱支援灾区,他们捐款的数额分别是(单位:元):100,45,100,40,100,60,155.下面有四个推断:
①这7名同学所捐的零花钱的平均数是150;
②这7名同学所捐的零花钱的中位数是100;
③这7名同学所捐的零花钱的众数是100;
④由这7名同学所捐的零花钱的中位数是100,可以推断该校全体同学所捐的零花钱的中位数也一定是100.
所有合理推断的序号是( )
A.①③B.②③C.②④D.②③④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com