
【题目】已知抛物线y=ax2+bx+a+2(a≠0)与x轴交于点A(x1,0),点B(x2,0),(点A在点B的左侧),抛物线的对称轴为直线x=-1.
(1)若点A的坐标为(-3,0),求抛物线的表达式及点B的坐标;
(2)C是第三象限的点,且点C的横坐标为-2,若抛物线恰好经过点C,直接写出x2的取值范围;
(3)抛物线的对称轴与x轴交于点D,点P在抛物线上,且∠DOP=45°,若抛物线上满足条件的点P恰有4个,结合图象,求a的取值范围.
【答案】(1)![]() ,(1,0);(2)-1<x2<0;(3)a<-2.
,(1,0);(2)-1<x2<0;(3)a<-2.
【解析】
(1)由题意可知抛物线的对称轴为![]() ,求出b=2a,将点A的坐标代入抛物线的表达式,即可求解;
,求出b=2a,将点A的坐标代入抛物线的表达式,即可求解;
(2)根据题意可得点C在第三象限,即点A在点C和函数对称轴之间,故-2<x1<-1,继而进行分析即可求解;
(3)根据题意可得满足条件的P在x轴的上方有2个,在x轴的下方也有2个,则抛物线与y轴的交点在x轴的下方,即可求解.
解:(1)抛物线的对称轴为![]() ,解得:b=2a,
,解得:b=2a,
故y=ax2+bx+a+2=a(x+1)2+2,
将点A的坐标代入上式并解得:![]() ,
,
故抛物线的表达式为:![]() ;
;
令y=0,即![]() ,解得:x=-3或1,
,解得:x=-3或1,
故点B的坐标为:(1,0).
(2)由(1)知:![]() ,
,
点C在第三象限,即点C在点A的下方,
即点A在点C和函数对称轴之间,故-2<x1<-1,
而![]() ,即x2=-2-x1,
,即x2=-2-x1,
故-1<x2<0.
(3)∵抛物线的顶点为(-1,2),
∴点D(-1,0),
∵∠DOP=45°,若抛物线上满足条件的点P恰有4个,
∴抛物线与x轴的交点在原点的左侧,如下图,

∴满足条件的P在x轴的上方有2个,在x轴的下方也有2个,
则抛物线与y轴的交点在x轴的下方,
当x=0时,![]() ,
,
解得:a<-2,
故a的取值范围为:a<-2.


 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案科目:初中数学 来源: 题型:
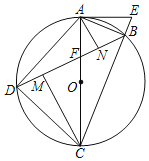
【题目】如图,四边形ABCD内接于⊙O,对角线AC、BD相交于点F,AC是⊙O的直径,延长CB到点E,连接AE,∠BAE=∠ADB,AN⊥BD,CM⊥BD,垂足分别为点N、M.
(1)证明:AE是⊙O的切线;
(2)试探究DM与BN的数量关系并证明;
(3)若BD=BC,MN=2DM,当AE=![]() 时,求OF的长.
时,求OF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】五一前夕,某时装店老板到厂家选购![]() 两种品牌的时装,若购进
两种品牌的时装,若购进![]() 品牌的时装
品牌的时装![]() 套,
套,![]() 品牌的时装
品牌的时装![]() 套,需要
套,需要![]() 元;若购进
元;若购进![]() 品牌的时装
品牌的时装![]() 套,
套,![]() 品牌的时装
品牌的时装![]() 套,需要
套,需要![]() 元.
元.
(1)求![]() 两种品牌的时装每套进价分别为多少元?
两种品牌的时装每套进价分别为多少元?
(2)若![]() 套
套![]() 品牌的时装售价
品牌的时装售价![]() 元,
元,![]() 套
套![]() 品牌的时装售价
品牌的时装售价![]() 元,时装店将购进的
元,时装店将购进的![]() 两种时装共
两种时装共![]() 套全部售出,所获利润要不少于
套全部售出,所获利润要不少于![]() 元,问
元,问![]() 品牌时装至少购进多少套?
品牌时装至少购进多少套?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明星期天上午8:00从家出发到离家36千米的书城买书,他先从家出发骑公共自行车到公交车站,等了12分钟的车,然后乘公交车于9:48分到达书城(假设在整个过程中小明骑车的速度不变,公交车匀速行驶,小明家、公交车站、书城依次在一条笔直的公路旁).如图是小明从家出发离公交车站的路程y(千米)与他从家出发的时间x(时)之间的函数图象,其中线段AB对应的函教表达式为y=kx+6.
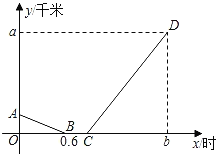
(1)求小明骑公共自行车的速度;
(2)求线段CD对应的函数表达式;
(3)求出发时间x在什么范围时,小明离公交车站的路程不超过3千米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】先阅读下列材料,再解答问题.
尺规作图
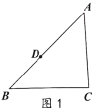
已知:△ABC,D是边AB上一点,如图1,
求作:四边形DBCF,使得四边形DBCF是平行四边形.
小明的做法如下:
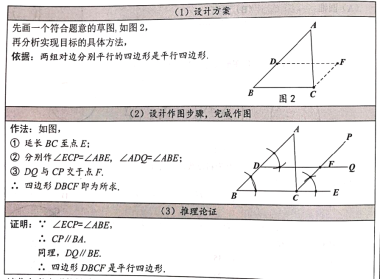
请你参考小明的做法,再设计一一种尺规作图的方法(与小明的方法不同),使得画出的四边形DBCF是平行四边形,并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
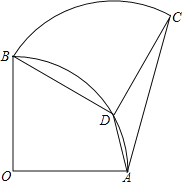
【题目】如图,扇形OAB中,∠AOB=90°,将扇形OAB绕点B逆时针旋转,得到扇形BDC,若点O刚好落在弧AB上的点D处,则![]() 的值为( )
的值为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
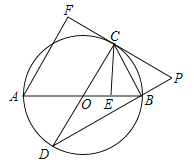
【题目】(2017广东省)如图,AB是⊙O的直径,AB=![]() ,点E为线段OB上一点(不与O,B重合),作CE⊥OB,交⊙O于点C,垂足为点E,作直径CD,过点C的切线交DB的延长线于点P,AF⊥PC于点F,连接CB.
,点E为线段OB上一点(不与O,B重合),作CE⊥OB,交⊙O于点C,垂足为点E,作直径CD,过点C的切线交DB的延长线于点P,AF⊥PC于点F,连接CB.
(1)求证:CB是∠ECP的平分线;
(2)求证:CF=CE;
(3)当![]() 时,求劣弧
时,求劣弧![]() 的长度(结果保留π)
的长度(结果保留π)
查看答案和解析>>
科目:初中数学 来源: 题型:
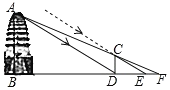
【题目】如图,西安市荐福寺内的小雁塔,是中国早期方形密檐式砖塔的典型作品,并作为丝绸之路的一处重要遗址点,被列入《世界遗产名录》.某周末,小乐和小夏相约去小雁塔游玩,在休息时,他们想利用所学知识测量小雁塔的高度,于是他们向工作人员借来测量工具由于观测点与小雁塔底部间的距离不易测量,于是他们利用太阳光照射影子进行测量,小乐先在小雁塔的影子顶端![]() 处竖直立一根长1.72米的木棒
处竖直立一根长1.72米的木棒![]() ,并测得此时木棒的影长
,并测得此时木棒的影长![]() 米;然后小夏在
米;然后小夏在![]() 的延长线上找出一点
的延长线上找出一点![]() ,使得
,使得![]() 、
、![]() 、
、![]() 三点在同一直线上,并测得
三点在同一直线上,并测得![]() 米已知图中所有点均在同一平面内,
米已知图中所有点均在同一平面内,![]() ,
,![]() ,根据以上测量过程及数据,请你帮他们求出小雁塔的高度
,根据以上测量过程及数据,请你帮他们求出小雁塔的高度![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】改革开放以来,人们的支付方式发生了巨大转变,近年来,移动支付已成为主要的支付方式之一,为了解某校学生上个月![]() 两种移动支付方式的使用情况,从全校
两种移动支付方式的使用情况,从全校![]() 名学生中随机抽取了
名学生中随机抽取了![]() 人,发现样本中
人,发现样本中![]() 两种支付方式都不使用的有
两种支付方式都不使用的有![]() 人,样本中仅使用
人,样本中仅使用![]() 种支付方式和仅使用
种支付方式和仅使用![]() 种支付方式的学生的支付金额
种支付方式的学生的支付金额![]() (元)的分布情况如下:
(元)的分布情况如下:
支付金额 支付方式 |
|
|
|
仅使用 |
|
|
|
仅使用 |
|
|
|
下面有四个推断:
①从样本中使用移动支付的学生中随机抽取一名学生,该生使用A支付方式的概率大于他使用B支付方式的概率;
②根据样本数据估计,全校1000名学生中.同时使用A、B两种支付方式的大约有400人;
③样本中仅使用A种支付方式的同学,上个月的支付金额的中位数一定不超过1000元;
④样本中仅使用B种支付方式的同学,上个月的支付金额的平均数一定不低于1000元.其中合理的是( )
A.①③B.②④C.①②③D.①②③④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com