
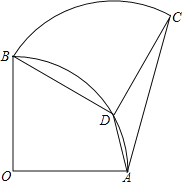
【题目】如图,扇形OAB中,∠AOB=90°,将扇形OAB绕点B逆时针旋转,得到扇形BDC,若点O刚好落在弧AB上的点D处,则![]() 的值为( )
的值为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】A
【解析】
如图,连OD、AB、BC,延长AD交BC于H点,由旋转的性质可得BD=BO=OD=CD=OA,∠BDC=90°,可证△ABC是等边三角形,由线段垂直平分线的性质可得AH垂直平分BC,由等腰直角三角形的性质和等边三角形的性质可得AC=2CH,AD=![]() CH-CH,即可求解.
CH-CH,即可求解.
解:如图,连OD、AB、BC,延长AD交BC于H点,
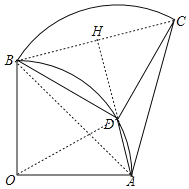
∵将扇形OAB绕点B逆时针旋转,得到扇形BDC,若点O刚好落在弧AB上的点D处,
∴BD=BO=OD=CD=OA,∠BDC=90°
∴∠OBD=60°,即旋转角为60°,
∴∠ABC=60°,又可知AB=BC,
∴△ABC是等边三角形,
∵AB=AC,BD=CD,
∴AH垂直平分BC,
∴∠CAH=30°,
∴AC=2CH,AH=![]() CH,
CH,
∵BD=CD,∠BDC=90°,DH⊥BC,
∴DH=CH,
∴AD=![]() CH﹣CH,
CH﹣CH,
∴![]() =
=![]() .
.
故选:A.


科目:初中数学 来源: 题型:
【题目】抗击新冠肺炎期间,某小区为方便管理,为居民设计了一个身份识别图案系统:在4×4的正方形网格中,白色正方形表示数字1,黑色正方形表示数字0,将第i行第j列表示的数记为ai,j(其中i,j都是不大于4的正整数),例如,图1中,a1,2=0.对第i行使用公式Ai=ai,1×23+ai,2×22+ai,3×21+ai,4×20进行计算,所得结果A1,A2,A3,A4分别表示居民楼号,单元号,楼层和房间号.例如,图1中,A3=a3,1×23+a3,2×22+a3,3×21+a3,4×20=1×8+0×4+0×2+1×1=9,A4=0×8+0×4+1×2+1×1=3,说明该居民住在9层,3号房间,即903号.
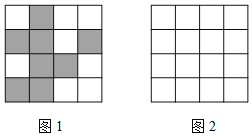
(1)图1中,a1,3= ;
(2)图1代表的居民居住在 号楼 单元;
(3)请仿照图1,在图2中画出8号楼4单元602号居民的身份识别图案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两家商场平时以同样的价格出售相同的商品.“五一”节期间两家商场都让利酬宾.在甲商场按累计购物金额的![]() 收费;在乙商场累计购物金额超过
收费;在乙商场累计购物金额超过![]() 元后,超出
元后,超出![]() 元的部分按
元的部分按![]() 收费.设小红在同一商场累计购物金额为
收费.设小红在同一商场累计购物金额为![]() 元,其中
元,其中![]() .
.
(1)根据题意,填写下表(单位:元):
累计购物金额 |
|
|
| ··· |
在甲商场实际花费 |
| ··· | ||
在乙商场实际花费 |
| ··· |
(2)设小红在甲商场实际花费![]() 元,在乙商场实际花费
元,在乙商场实际花费![]() 元,分别求
元,分别求![]() 关于
关于![]() 的函数解析式;
的函数解析式;
(3)“五一”节期间小红如何选择这两家商场去购物更省钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某景区为了解游客人数的变化规律,提高旅游服务质量,收集并整理了某月(30天)接待游客人数(单位:万人)的数据,绘制了下面的统计图和统计表:
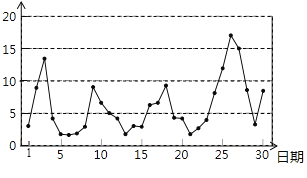
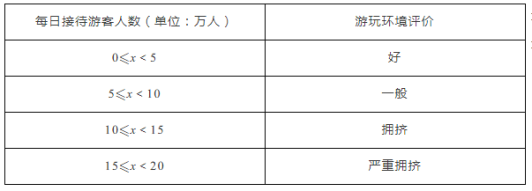
根据以上信息,以下四个判断中,正确的是_________.(填写所有正确结论的序号)
①该景区这个月游玩环境评价为“拥挤或严重拥挤”的天数仅有4天;
②该景区这个月每日接待游客人数的中位数在5~10广域网人之间;
③该景区这个月平均每日接待游客人数低于5万人;
④这个月1日至5日的五天中,如果某人曾经随机选择其中的两天到该景区游玩,那么他“这两天游玩环境评价均为好”的可能性为![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=ax2+bx+a+2(a≠0)与x轴交于点A(x1,0),点B(x2,0),(点A在点B的左侧),抛物线的对称轴为直线x=-1.
(1)若点A的坐标为(-3,0),求抛物线的表达式及点B的坐标;
(2)C是第三象限的点,且点C的横坐标为-2,若抛物线恰好经过点C,直接写出x2的取值范围;
(3)抛物线的对称轴与x轴交于点D,点P在抛物线上,且∠DOP=45°,若抛物线上满足条件的点P恰有4个,结合图象,求a的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,对角线AC、BD相交于点O,过点D作对角线BD的垂线交BA的延长线于点E.
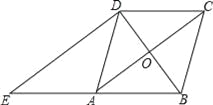
(1)证明:四边形ACDE是平行四边形;
(2)若AC=8,BD=6,求△ADE的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校在开展读书交流活动中,全体师生积极捐书,为了解所捐书籍的种类,对部分书籍进行了抽样调查,张老师根据调查数据绘制了如下不完整的统计图.
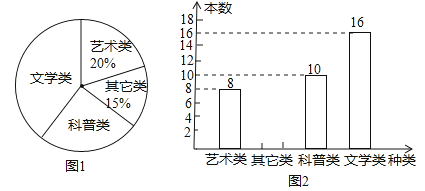
请根据统计图回答下列问题:
(1)本次抽样调查的书籍有多少本?
(2)试求图1中表示文学类书籍的扇形圆心角的度数,并补全条形统计图.
(3)本次活动师生共捐书![]() 本,请估计有多少本科普类书籍?
本,请估计有多少本科普类书籍?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知锐角∠AOB,如图,(1)在射线OA上取一点C,以点O为圆心,OC长为半径作![]() ,交射线OB于点D,连接CD;(2)分别以点C,D为圆心,CD长为半径作弧,两弧交于点P,连接CP,DP;(3)作射线OP交CD于点Q.根据以上作图过程及所作图形,下列结论中错误的是( )
,交射线OB于点D,连接CD;(2)分别以点C,D为圆心,CD长为半径作弧,两弧交于点P,连接CP,DP;(3)作射线OP交CD于点Q.根据以上作图过程及所作图形,下列结论中错误的是( )
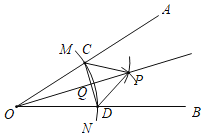
A.CP∥OBB.CP=2QCC.∠AOP=∠BOPD.CD⊥OP
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com