
【题目】抗击新冠肺炎期间,某小区为方便管理,为居民设计了一个身份识别图案系统:在4×4的正方形网格中,白色正方形表示数字1,黑色正方形表示数字0,将第i行第j列表示的数记为ai,j(其中i,j都是不大于4的正整数),例如,图1中,a1,2=0.对第i行使用公式Ai=ai,1×23+ai,2×22+ai,3×21+ai,4×20进行计算,所得结果A1,A2,A3,A4分别表示居民楼号,单元号,楼层和房间号.例如,图1中,A3=a3,1×23+a3,2×22+a3,3×21+a3,4×20=1×8+0×4+0×2+1×1=9,A4=0×8+0×4+1×2+1×1=3,说明该居民住在9层,3号房间,即903号.
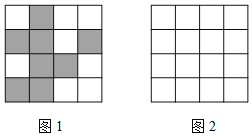
(1)图1中,a1,3= ;
(2)图1代表的居民居住在 号楼 单元;
(3)请仿照图1,在图2中画出8号楼4单元602号居民的身份识别图案.
【答案】(1)1;(2)11,2;(3)图见解析.
【解析】
(1)根据白色正方形表示数字1,黑色正方形表示数字0,第i行第j列表示的数记为![]() ,观察图形即可得答案;
,观察图形即可得答案;
(2)![]() 分别表示居民楼号,单元号,按照题中公式计算即可;
分别表示居民楼号,单元号,按照题中公式计算即可;
(3)按照题中公式及8号楼4单元602房间求出![]() 的值,然后画图即可.
的值,然后画图即可.
(1)由题意得:![]() 表示第一行第三列的数
表示第一行第三列的数
由图1可知,第一行第三列为白色正方形,表示数字1,则![]()
故答案为:1;
(2)![]()
![]()
![]()
![]()
![]()
![]()
![]()
则图1代表的居民居住在11号楼2单元
故答案为:11,2;
(3)由题意得:![]() 只能等于1或0,
只能等于1或0,![]()
![]()
![]()
解得![]()
则第一行正方形的颜色依次为白色、黑色、黑色、黑色
![]()
![]()
解得![]()
则第二行正方形的颜色依次为黑色、白色、黑色、黑色
![]()
![]()
解得![]()
则第三行正方形的颜色依次为黑色、白色、白色、黑色
![]()
![]()
解得![]()
则第四行正方形的颜色依次为黑色、黑色、白色、黑色
因此,8号楼4单元602房间居民的身份识别图案如下图所示:



科目:初中数学 来源: 题型:
【题目】为调查广西北部湾四市市民上班时最常用的交通工具的情况,随机抽取了四市部分市民进行调查,要求被调查者从“A:自行车,B:电动车,C:公交车,D:家庭汽车,E:其他”五个选项中选择最常用的一项,将所有调查结果整理后绘制成如下不完整的条形统计图和扇形统计图,请结合统计图回答下列问题:

(1)在这次调查中,一共调查了 名市民,扇形统计图中,C组对应的扇形圆心角是 °;
(2)请补全条形统计图;
(3)若甲、乙两人上班时从A、B、C、D四种交通工具中随机选择一种,则甲、乙两人恰好选择同一种交通工具上班的概率是多少?请用画树状图或列表法求解.
查看答案和解析>>
科目:初中数学 来源: 题型:
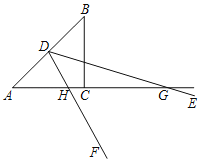
【题目】如图,在等腰Rt△ABC中,AC=BC=6![]() ,∠EDF的顶点D是AB的中点,且∠EDF=45°,现将∠EDF绕点D旋转一周,在旋转过程中,当∠EDF的两边DE、DF分别交直线AC于点G、H,把△DGH沿DH折叠,点G落在点M处,连接AM,若
,∠EDF的顶点D是AB的中点,且∠EDF=45°,现将∠EDF绕点D旋转一周,在旋转过程中,当∠EDF的两边DE、DF分别交直线AC于点G、H,把△DGH沿DH折叠,点G落在点M处,连接AM,若![]() =
=![]() ,则AH的长为_______.
,则AH的长为_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
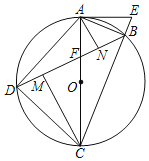
【题目】如图,四边形ABCD内接于⊙O,对角线AC、BD相交于点F,AC是⊙O的直径,延长CB到点E,连接AE,∠BAE=∠ADB,AN⊥BD,CM⊥BD,垂足分别为点N、M.
(1)证明:AE是⊙O的切线;
(2)试探究DM与BN的数量关系并证明;
(3)若BD=BC,MN=2DM,当AE=![]() 时,求OF的长.
时,求OF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,抛物线y=ax2+bx﹣3a(a≠0)经过点A(﹣1,0).
(1)求抛物线的顶点坐标;(用含a的式子表示)
(2)已知点B(3,4),将点B向左平移3个单位长度,得到点C.若抛物线与线段BC恰有一个公共点,结合函数的图象,求a的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】星期天8:00~8:30,燃气公司给平安加气站的储气罐注入天然气,注完气后,一位工作人员以每车20米![]() 的加气量,依次给在加气站排队等候的若干辆车加气储气罐中的储气量
的加气量,依次给在加气站排队等候的若干辆车加气储气罐中的储气量![]() (米
(米![]() )与时间
)与时间![]() (小时)的函数关系式如图所示:
(小时)的函数关系式如图所示:
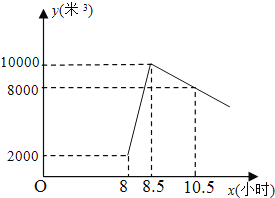
(1)8:00~8:30,燃气公司向储气罐注入了______米![]() 的天然气;
的天然气;
(2)当![]() 时,求储气罐中的储气量(米
时,求储气罐中的储气量(米![]() )与时间
)与时间![]() (小时)的函数关系式;
(小时)的函数关系式;
(3)正在排队等候的第20辆车加完后储气罐内还有天然气______米![]() ,这20辆车在当天9:00之前能加完气吗?请说明理由.
,这20辆车在当天9:00之前能加完气吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
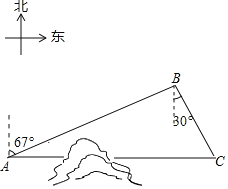
【题目】如图,C地在A地的正东方向,因有大山阻隔,由A地到C地需要绕行B地,已知B地位于A地北偏东67°方向,距离A地520km,C地位于B地南偏东30°方向,若打通穿山隧道,建成两地直达高铁,求A地到C地之间高铁线路的长(结果保留整数)(参考数据:sin67°≈0.92;cos67°≈0.38;![]() ≈1.73)
≈1.73)
查看答案和解析>>
科目:初中数学 来源: 题型:
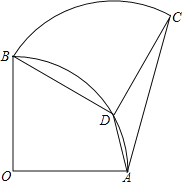
【题目】如图,扇形OAB中,∠AOB=90°,将扇形OAB绕点B逆时针旋转,得到扇形BDC,若点O刚好落在弧AB上的点D处,则![]() 的值为( )
的值为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com