
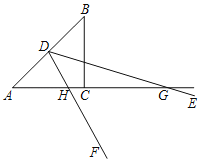
【题目】如图,在等腰Rt△ABC中,AC=BC=6![]() ,∠EDF的顶点D是AB的中点,且∠EDF=45°,现将∠EDF绕点D旋转一周,在旋转过程中,当∠EDF的两边DE、DF分别交直线AC于点G、H,把△DGH沿DH折叠,点G落在点M处,连接AM,若
,∠EDF的顶点D是AB的中点,且∠EDF=45°,现将∠EDF绕点D旋转一周,在旋转过程中,当∠EDF的两边DE、DF分别交直线AC于点G、H,把△DGH沿DH折叠,点G落在点M处,连接AM,若![]() =
=![]() ,则AH的长为_______.
,则AH的长为_______.
【答案】![]() 或
或![]() 或3
或3![]()
【解析】
分三种情形:①如图1中,当点H在线段AC上,点G在AC的延长线上时,连接CD,作DJ⊥AC于J,设AH=3k,AM=4k.②如图2中,当点H在线段AC上,点G在上时,连接CD,作DJ⊥AC于J,设AH=3k,AM=4k.③如图3中,当点H在线段CA的延长线上,点G在线段AC上时,连接CD,作DJ⊥AC于J,设AH=3k,AM=4k.首先证明AM⊥AC,利用相似三角形的性质以及勾股定理构建方程解决问题即可.
解:①如图1中,当点H在线段AC上,点G在AC的延长线上时,连接CD,作DJ⊥AC于J,设AH=3k,AM=4k.
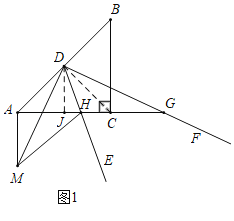
∵CA=CB,∠ACB=90°,AD=DB,
∴CD⊥AB,CD=DA=DB,
∴∠ACD=∠DCB=45°,∠DCG=135°,
∵∠EDF=∠EDM=45°,DG=DM,
∴∠ADC=∠MDG,
∴∠ADM=∠CDG,
∴△ADM≌△CDG(SAS),
∴∠DAM=∠DCG=135°,
∵∠CAB=45°,
∴∠CAM=90°,
∴MH=GH=![]() =
=![]() =5k,
=5k,
∵∠GDH=∠GAD=45°,∠DGH=∠AGD,
∴△DGH∽△AGD,
∴![]() =
=![]() ,
,
∴DG2=GHGA=40k2,
∵AC=BC=6![]() ,∠ACB=90°,
,∠ACB=90°,
∴AB=![]() AC=12,
AC=12,
∴AD=CD=6,
∵DJ⊥AC,
∴AJ=JC=3![]() ,DJ=AJ=IC=3
,DJ=AJ=IC=3![]() ,
,
∴GJ=8K﹣3![]() ,
,
在Rt△DJG中,∵DG2=DJ2+GJ2,
∴40k2=(8k﹣3![]() )2+(3
)2+(3![]() )2,
)2,
解得k=![]() 或
或![]() (舍弃),
(舍弃),
∴AH=3k=![]() .
.
②如图2中,当点H在线段AC上,点G在上时,连接CD,作DJ⊥AC于J,设AH=3k,AM=4k.
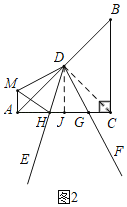
同法可得:40k2=(8k﹣3![]() )2+(3
)2+(3![]() )2,
)2,
解得k=![]() (舍弃)或
(舍弃)或![]() ,
,
∴AH=3k=![]() .
.
③如图3中,当点H在线段CA的延长线上,点G在线段AC上时,连接CD,作DJ⊥AC于J,设AH=3k,AM=4k.
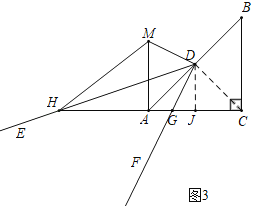
同法可得:10k2=(3![]() ﹣2k)2+(3
﹣2k)2+(3![]() )2,
)2,
解得k=![]() 或﹣3
或﹣3![]() (舍弃),
(舍弃),
∴AH=3k=3![]() ,
,
综上所述,满足条件的AH的值为![]() 或
或![]() 或3
或3![]() .
.
故答案为![]() 或
或![]() 或3
或3![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,在△![]() 中,高
中,高![]() =3,∠
=3,∠![]() =45°,
=45°,![]() =
=![]() ,动点
,动点![]() 从点
从点![]() 出发,沿
出发,沿![]() 方向以每秒1个单位长度的速速向终点
方向以每秒1个单位长度的速速向终点![]() 运动,当点
运动,当点![]() 与点
与点![]() 、
、![]() 不重合时,过点
不重合时,过点![]() 作
作![]() 、
、![]() 的平行线,与
的平行线,与![]() 分别交于点
分别交于点![]() 、
、![]() ,将△
,将△![]() 绕
绕![]() 的中点旋转180°得△
的中点旋转180°得△![]() ,设点
,设点![]() 的运动时间为
的运动时间为![]() 秒,△
秒,△![]() 与△
与△![]() 重叠部分面积为
重叠部分面积为![]() .
.
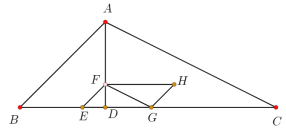
(1)当![]() = 秒时,点
= 秒时,点![]() 落在
落在![]() 边上.
边上.
(2)求![]() 与
与![]() 的函数关系式.
的函数关系式.
(3)当直线![]() 将△
将△![]() 分为面积比为1:3的两部分时,直接写出
分为面积比为1:3的两部分时,直接写出![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题提出:
如图所示,有三根针和套在一根针上的若干金属片,按下列规则,把金属片从一根针上全部移到另一根针上.

a.每次只能移动1个金属片;
b.较大的金属片不能放在较小的金属片上面.
把![]() 个金属片从1号针移到3号针,最少移动多少次?
个金属片从1号针移到3号针,最少移动多少次?
问题探究:为了探究规律,我们采用一般问题特殊化的方法,先从简单的情形入手,再逐次递进,最后得出一般性结论.
探究一:当![]() 时,只需把金属片从1号针移到3号针,用符号
时,只需把金属片从1号针移到3号针,用符号![]() 表示,共移动了1次.
表示,共移动了1次.
探究二:当![]() 时,为了避免将较大的金属片放在较小的金属片上面,我们利用2号针作为“中间针”,移动的顺序是:
时,为了避免将较大的金属片放在较小的金属片上面,我们利用2号针作为“中间针”,移动的顺序是:
a.把第1个金属片从1号针移到2号针;
b.把第2个金属片从1号针移到3号针;
c.把第1个金属片从2号针移到3号针.
用符号表示为:![]() ,
,![]() ,
,![]() .共移动了3次.
.共移动了3次.
探究三:当![]() 时,把上面两个金属片作为一个整体,则归结为
时,把上面两个金属片作为一个整体,则归结为![]() 的情形,移动的顺序是:
的情形,移动的顺序是:
a.把上面两个金属片从1号针移到2号针;
b.把第3个金属片从1号针移到3号针;
c.把上面两个金属片从2号针移到3号针.
其中(1)和(3)都需要借助中间针,用符号表示为:
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .共移动了7次.
.共移动了7次.
(1)探究四:请仿照前面步骤进行解答:当![]() 时,把上面3个金属片作为一个整体,移动的顺序是:___________________________________________________.
时,把上面3个金属片作为一个整体,移动的顺序是:___________________________________________________.
(2)探究五:根据上面的规律你可以发现当![]() 时,需要移动________次.
时,需要移动________次.
(3)探究六:把![]() 个金属片从1号针移到3号针,最少移动________次.
个金属片从1号针移到3号针,最少移动________次.
(4)探究七:如果我们把![]() 个金属片从1号针移到3号针,最少移动的次数记为
个金属片从1号针移到3号针,最少移动的次数记为![]() ,当
,当![]() 时如果我们把
时如果我们把![]() 个金属片从1号针移到3号针,最少移动的次数记为
个金属片从1号针移到3号针,最少移动的次数记为![]() ,那么
,那么![]() 与
与![]() 的关系是
的关系是![]() __________.
__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点A(﹣3,y1),B(2,y2)均在抛物线y=ax2+bx+c上,点P(m,n)是该抛物线的顶点,若y1>y2≥n,则m的取值范围是( )
A.﹣3<m<2B.﹣![]() <m<-
<m<-![]() C.m>﹣
C.m>﹣![]() D.m>2
D.m>2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c经过点B(4,0),C(0,﹣2),对称轴为直线x=1,与x轴的另一个交点为点A.
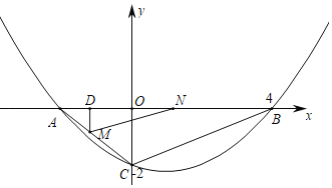
(1)求抛物线的解析式;
(2)点M从点A出发,沿AC向点C运动,速度为1个单位长度/秒,同时点N从点B出发,沿BA向点A运动,速度为2个单位长度/秒,当点M、N有一点到达终点时,运动停止,连接MN,设运动时间为t秒,当t为何值时,AMN的面积S最大,并求出S的最大值;
(3)点P在x轴上,点Q在抛物线上,是否存在点P、Q,使得以点P、Q、B、C为顶点的四边形是平行四边形,若存在,直接写出所有符合条件的点P坐标,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】成都市天府一南站城市立交桥是成都市政府确定的城建标志性建筑,如图是立交桥引申出的部分平面图,测得拉索AB与水平桥面的夹角是37°,拉索DE与水平桥面的夹角是67°,两拉索顶端的距离AD为2m,两拉索底端距离BE为10m,请求出立柱AC的长.(参考数据tan37°≈![]() ,sin37°≈
,sin37°≈![]() ,cos37°≈
,cos37°≈![]() ,tan67°≈
,tan67°≈![]() ,sin67°≈
,sin67°≈![]() ,cos67°≈
,cos67°≈![]() )
)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抗击新冠肺炎期间,某小区为方便管理,为居民设计了一个身份识别图案系统:在4×4的正方形网格中,白色正方形表示数字1,黑色正方形表示数字0,将第i行第j列表示的数记为ai,j(其中i,j都是不大于4的正整数),例如,图1中,a1,2=0.对第i行使用公式Ai=ai,1×23+ai,2×22+ai,3×21+ai,4×20进行计算,所得结果A1,A2,A3,A4分别表示居民楼号,单元号,楼层和房间号.例如,图1中,A3=a3,1×23+a3,2×22+a3,3×21+a3,4×20=1×8+0×4+0×2+1×1=9,A4=0×8+0×4+1×2+1×1=3,说明该居民住在9层,3号房间,即903号.
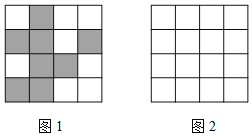
(1)图1中,a1,3= ;
(2)图1代表的居民居住在 号楼 单元;
(3)请仿照图1,在图2中画出8号楼4单元602号居民的身份识别图案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,半径为5的⊙A中,弦BC,ED所对的圆心角分别是∠BAC,∠EAD.已知DE=6,∠BAC+∠EAD=180°,则弦BC的弦心距等于 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某景区为了解游客人数的变化规律,提高旅游服务质量,收集并整理了某月(30天)接待游客人数(单位:万人)的数据,绘制了下面的统计图和统计表:
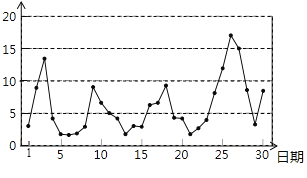
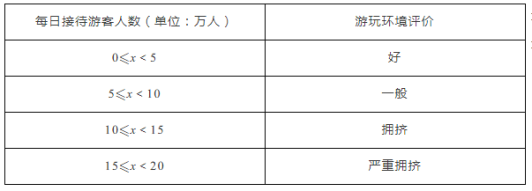
根据以上信息,以下四个判断中,正确的是_________.(填写所有正确结论的序号)
①该景区这个月游玩环境评价为“拥挤或严重拥挤”的天数仅有4天;
②该景区这个月每日接待游客人数的中位数在5~10广域网人之间;
③该景区这个月平均每日接待游客人数低于5万人;
④这个月1日至5日的五天中,如果某人曾经随机选择其中的两天到该景区游玩,那么他“这两天游玩环境评价均为好”的可能性为![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com