
【题目】如图,在△![]() 中,高
中,高![]() =3,∠
=3,∠![]() =45°,
=45°,![]() =
=![]() ,动点
,动点![]() 从点
从点![]() 出发,沿
出发,沿![]() 方向以每秒1个单位长度的速速向终点
方向以每秒1个单位长度的速速向终点![]() 运动,当点
运动,当点![]() 与点
与点![]() 、
、![]() 不重合时,过点
不重合时,过点![]() 作
作![]() 、
、![]() 的平行线,与
的平行线,与![]() 分别交于点
分别交于点![]() 、
、![]() ,将△
,将△![]() 绕
绕![]() 的中点旋转180°得△
的中点旋转180°得△![]() ,设点
,设点![]() 的运动时间为
的运动时间为![]() 秒,△
秒,△![]() 与△
与△![]() 重叠部分面积为
重叠部分面积为![]() .
.
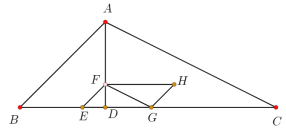
(1)当![]() = 秒时,点
= 秒时,点![]() 落在
落在![]() 边上.
边上.
(2)求![]() 与
与![]() 的函数关系式.
的函数关系式.
(3)当直线![]() 将△
将△![]() 分为面积比为1:3的两部分时,直接写出
分为面积比为1:3的两部分时,直接写出![]() 的值.
的值.
【答案】(1)![]() ;(2)当0<1≤
;(2)当0<1≤![]() 时,
时,![]() ;
;![]() <t<3时,S=
<t<3时,S=![]() ;(3)t=
;(3)t=![]() 或t=
或t=![]()
【解析】
(1)由旋转的性质可得EH=FG=3t,再根据平行线分线段成比例可得![]() ,得到方程求解即可;
,得到方程求解即可;
(2)分0<1≤![]() 和
和![]() <t<3时,结合图形利用三角形面积计算公式即可得出函数关系;
<t<3时,结合图形利用三角形面积计算公式即可得出函数关系;
(3)根据“直线![]() 将△
将△![]() 分为面积比为1:3的两部分”分两种情况由BG:BC=1:2与BG:BC=
分为面积比为1:3的两部分”分两种情况由BG:BC=1:2与BG:BC=![]() :2时求出t的值即可.
:2时求出t的值即可.
(1)当点H落在AC边上时,如图1,
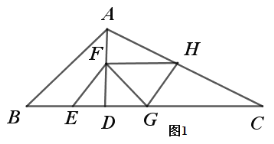
∵AD ⊥BC,∠B=45°
∴△ABD为等腰直角三角形,
∵FE// AB,
∴△FED为等腰直角三角形,
∴ED=FD=t,
又∵FG//AC,
∴∠FGD=∠C,
∴tan∠FGD=tan C=![]()
∴DG=2t,
∴EG=3t
又∵△HG由△EFG旋转得到,
FH=EG=3t, 四边形FE GH为平行四边形,
∴FH //BC,
∴![]()
∴![]() ,解得,t=
,解得,t=![]() ,
,
即当t=![]() 秒时,点H落在AC边上.
秒时,点H落在AC边上.
故答案为:![]() ;
;
(2) ①当0<1≤![]() 时, 如图2, 重叠部分图形为A HGF,
时, 如图2, 重叠部分图形为A HGF,
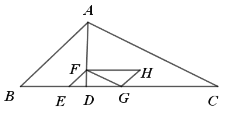
图2
∴![]()
②当![]() <t<3时, 如图3,重叠部分图形为四边形MFG N,
<t<3时, 如图3,重叠部分图形为四边形MFG N,
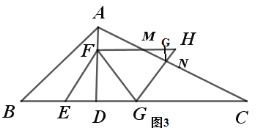
![]() ,
,![]()
![]()
![]()
![]()
![]() ,
,
![]()
![]()
![]()
过N作![]() 于K,
于K,
![]()
![]()
![]()
![]()
![]()
![]()
![]()
=![]()
(3)①当BG:BC=1:2时, 如图4,

此时KG为△ABC的中位线,S△BKG:S四边形AKGC=1:3,
∵AD=3,∠ABD=45°,AD⊥BC
∴BD=AD=3,
∵KG//AC,
∴∠C=∠KGB,tanC=![]() ,
,
∴tan∠KGB =![]() ,
,
∴DG=2t,DC=6
∴BC=9,
∴![]() ,解得,t=
,解得,t=![]() ;
;
②当BG:BC=![]() :2时,如图5,此时S四边形AKGC:S△BKG=1:3,
:2时,如图5,此时S四边形AKGC:S△BKG=1:3,

∴![]() ,解得,t=
,解得,t=![]()
综上, 当直线FG将△ABC分为面积比为1:3的两部分时,t=![]() 或t=
或t=![]() .
.


科目:初中数学 来源: 题型:
【题目】如图①,在矩形ABCD中,AB=6,BC=9,点E是BC边上一动点,连接AE、DE ,作△ECD的外接⊙O,交AD于点F,交AE于点G,连接FG.
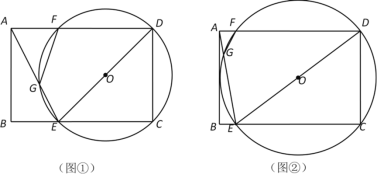
(1)求证△AFG∽△AED;
(2)当BE的长为 时,△AFG为等腰三角形;
(3)如图②,若BE=1,求证:AB与⊙O相切.
查看答案和解析>>
科目:初中数学 来源: 题型:
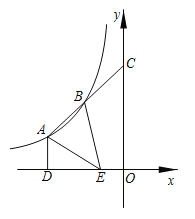
【题目】如图,A,B是反比例函数![]() (k≠0)图象上的两点,延长线段AB交y轴于点C,且B为线段AC的中点,过点A作AD⊥x轴于点D,E为线段OD的三等分点,且OE<DE.连接AE,BE.若S△ABE=7,则k的值为_________.
(k≠0)图象上的两点,延长线段AB交y轴于点C,且B为线段AC的中点,过点A作AD⊥x轴于点D,E为线段OD的三等分点,且OE<DE.连接AE,BE.若S△ABE=7,则k的值为_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
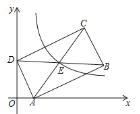
【题目】在平面直角坐标系中,矩形![]() 的顶点
的顶点![]() (1,0),
(1,0),![]() (0,2),点
(0,2),点![]() 在第一象限,
在第一象限,![]() ∥
∥![]() 轴,若函数
轴,若函数![]() =
=![]() 的图象经过矩形
的图象经过矩形![]() 的对角线的交点,则
的对角线的交点,则![]() 的值为( )
的值为( )
A.4B.5C.8D.10
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某初中学校餐厅为了解学生对早餐的要求,随即抽样调查了该校的部分学生,并根据其中两个单选问题的调查结果,绘制了如下尚不完整的统计图表.
学生能接受的早餐价格统计表
价格分组(单位:元) | 频数 | 频率 |
0<x≤2 | 60 | 0.15 |
2<x≤4 | 180 | c |
4<x≤6 | 92 | 0.23 |
6<x≤8 | a | 0.12 |
x>8 | 20 | 0.05 |
合计 | b | 1 |
根据以上信息解答下列问题:
(1)统计表中,a= ,b= ,c= .
(2)扇形统计图中,m的值为 ,“甜”所对应的圆心角的度数是 .
(3)该餐厅计划每天提供早餐2000份,其中咸味大约准备多少份较好?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙、丙、丁四人做传球游戏:第一次由甲将球随机传给乙、丙、丁中的某一人,第二次由持球者将球再随机传给其他三人中的某一人.
(1)第一次传球后球到乙手里的概率为 ;
(2)画树状图或列表求第二次传球后球回到甲手里的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
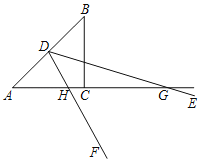
【题目】如图,在等腰Rt△ABC中,AC=BC=6![]() ,∠EDF的顶点D是AB的中点,且∠EDF=45°,现将∠EDF绕点D旋转一周,在旋转过程中,当∠EDF的两边DE、DF分别交直线AC于点G、H,把△DGH沿DH折叠,点G落在点M处,连接AM,若
,∠EDF的顶点D是AB的中点,且∠EDF=45°,现将∠EDF绕点D旋转一周,在旋转过程中,当∠EDF的两边DE、DF分别交直线AC于点G、H,把△DGH沿DH折叠,点G落在点M处,连接AM,若![]() =
=![]() ,则AH的长为_______.
,则AH的长为_______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com