
【题目】如图,平行四边形![]() ,点
,点![]() 是
是![]() 上的一点,连结
上的一点,连结![]() ,
,![]() ,
,![]() 平分
平分![]() ,交
,交![]() 于点
于点![]() ,且点
,且点![]() 是
是![]() 的中点,连结
的中点,连结![]() ,已知
,已知![]() ,
,![]() ,则
,则![]() ________.
________.
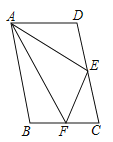
【答案】4
【解析】
如下图,延长AE与BC,交于点G,先证△ADE≌△GCE,得到CG=AD=5,再利用角度转化,得出△AFG是等腰三角形,最后在等腰△AFG中求得FE的长.
如下图,延长AE与BC,交于点G
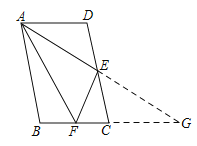
∵四边形ABCD是平行四边形,∴AD∥BC
∴∠DAE=∠CGE,∠ADE=∠GCE
∵点E是DC的中点,∴DE=EC
∴△ADE≌△GCE(AAS)
∴CG=AD=5,AE=EG
∵CF=3,∴FG=8
∵∠FAD=60°,AE是∠FAD的角平分线
∴∠FAE=∠EAD=30°,∴∠CGE=∠EAD=30°
∴∠FAE=∠FGE,△FAG是等腰三角形
∴AF=FG=8
∵AE=EG,△FAG是等腰三角形
∴EF⊥AG
∴△AEF是直角三角形,且AF=8,∠FAE=30°
∴EF=4
故答案为:4


 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案科目:初中数学 来源: 题型:
【题目】在![]() 中,
中,![]() ,点
,点![]() 分别是边
分别是边![]() 的中点,连接
的中点,连接![]() ,
,
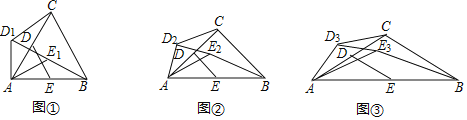
(1)如图①,当![]() 时,
时,![]() 绕点
绕点![]() 逆时针旋转得到
逆时针旋转得到![]() ,连接
,连接![]() 、
、![]() ,
,![]() 在旋转过程中请猜想:
在旋转过程中请猜想:![]() ______(直接写出答案);
______(直接写出答案);
(2)如图②,当![]() 时,
时,![]() 绕点
绕点![]() 逆时针旋转得到
逆时针旋转得到![]() ,连接
,连接![]() 、
、![]() ,
,![]() 在旋转过程中请猜想:
在旋转过程中请猜想:![]() 的比值,并证明你的猜想;
的比值,并证明你的猜想;
(3)如图③,当![]() 时,
时,![]() 绕点
绕点![]() 逆时针旋转得到
逆时针旋转得到![]() ,连接
,连接![]() 、
、![]() ,请直接写出
,请直接写出![]() 在旋转过程中
在旋转过程中![]() 的比值.(用含
的比值.(用含![]() 的代数式表示)
的代数式表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
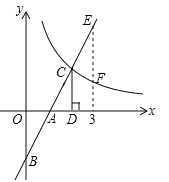
【题目】(3分)如图,在直角坐标系中,直线![]() 与坐标轴交于A、B两点,与双曲线
与坐标轴交于A、B两点,与双曲线![]() (
(![]() )交于点C,过点C作CD⊥x轴,垂足为D,且OA=AD,则以下结论:
)交于点C,过点C作CD⊥x轴,垂足为D,且OA=AD,则以下结论:
①![]() ;
;
②当0<x<3时,![]() ;
;
③如图,当x=3时,EF=![]() ;
;
④当x>0时,![]() 随x的增大而增大,
随x的增大而增大,![]() 随x的增大而减小.
随x的增大而减小.
其中正确结论的个数是( )
A.1 B.2 C.3 D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】两人要去某风景区游玩,每天某一时段开往该风景区有三辆汽车(票价相同),但是他们不知道这些车的舒适程度,也不知道汽车开过来的顺序.两人采用了不同的乘车方案:甲无论如何总是上开来的第一辆车.而乙则是先观察后上车,当第一辆车开来时,他不上车,而是仔细观察车的舒适状况.如果第二辆车的状况比第一辆好,他就上第二辆车;如果第二辆不比第一辆好,他就上第三辆车.如果把这三辆车的舒适程度分为上、中、下三等,请尝试解决下面的问题:请用树状图或列表法分析,甲、乙两人采用的方案,哪一种方案使自己乘坐上等车的可能性大.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:在平面直角坐标系![]() 中点
中点![]() 、
、![]() 是某函数图象上任意两点
是某函数图象上任意两点![]() .将函数图象中
.将函数图象中![]() 的部分沿直线
的部分沿直线![]() 作轴对称,
作轴对称,![]() 的部分沿直线
的部分沿直线![]() 作轴对称,与原函数图象中
作轴对称,与原函数图象中![]() 的部分组成了个新函数的图象,称这个新函数为原函数关于点
的部分组成了个新函数的图象,称这个新函数为原函数关于点![]() 、
、![]() 的“双对称函数”.
的“双对称函数”.
例如:如图①,点![]() 、
、![]() 是一次函数
是一次函数![]() 图象上的两个点,则函数
图象上的两个点,则函数![]() 关于点
关于点![]() 、
、![]() 的“双对称函数”的图象如图②所示.
的“双对称函数”的图象如图②所示.
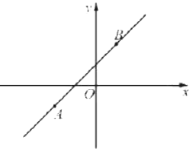
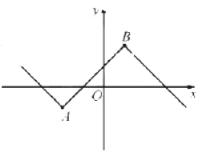
图① 图②
(1)点![]() 、
、![]() 是函数
是函数![]() 图象上的两点,
图象上的两点,![]() 关于点
关于点![]() 、
、![]() 的“双对称函数”的图象记作
的“双对称函数”的图象记作![]() .若
.若![]() 是中心对称图形,直接写出
是中心对称图形,直接写出![]() 的值.
的值.
(2)点![]() 、
、![]() 是二次函数
是二次函数![]() 图象上的两点,该二次函数关于点
图象上的两点,该二次函数关于点![]() 、
、![]() 的“双对称函数”记作
的“双对称函数”记作![]() .
.
①求![]() 、
、![]() 两点的坐标(用含
两点的坐标(用含![]() 的代数式表示).
的代数式表示).
②当![]() 时,求出函数
时,求出函数![]() 的解析式;
的解析式;
③若![]() 时,函数
时,函数![]() 的最小值为
的最小值为![]() ,求
,求![]() 时,
时,![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某种蔬菜的销售单价y1与销售月份x之间的关系如图1所示,成本y2与销售月份x之间的关系如图2所示(图1的图象是线段,图2的图象是抛物线)
(1)已知6月份这种蔬菜的成本最低,此时出售每千克的收益是多少元?(收益=售价﹣成本)
(2)哪个月出售这种蔬菜,每千克的收益最大?简单说明理由.
(3)已知市场部销售该种蔬菜4、5两个月的总收益为22万元,且5月份的销售量比4月份的销售量多2万千克,求4、5两个月的销售量分别是多少万千克?
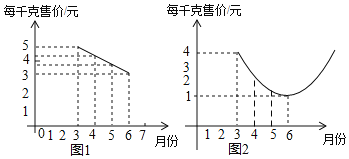
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某汽车专卖店销售A、B两种型号的新能源汽车.上周售出1辆A型车和3辆B型车,两种车型的销售总额为96万元;本周销售2辆A型车和1辆B型车,两种车型的销售总额为62万元,已知两种型号汽车销售价格始终不变.
(1)求A、B两种车型的销售单价分别是多少?
(2)第三周计划售出A、B两种型号的车共5辆,若销售总额不少于100万元,则B型车至少要售出多少辆?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△![]() 中,高
中,高![]() =3,∠
=3,∠![]() =45°,
=45°,![]() =
=![]() ,动点
,动点![]() 从点
从点![]() 出发,沿
出发,沿![]() 方向以每秒1个单位长度的速速向终点
方向以每秒1个单位长度的速速向终点![]() 运动,当点
运动,当点![]() 与点
与点![]() 、
、![]() 不重合时,过点
不重合时,过点![]() 作
作![]() 、
、![]() 的平行线,与
的平行线,与![]() 分别交于点
分别交于点![]() 、
、![]() ,将△
,将△![]() 绕
绕![]() 的中点旋转180°得△
的中点旋转180°得△![]() ,设点
,设点![]() 的运动时间为
的运动时间为![]() 秒,△
秒,△![]() 与△
与△![]() 重叠部分面积为
重叠部分面积为![]() .
.
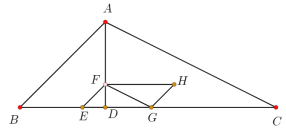
(1)当![]() = 秒时,点
= 秒时,点![]() 落在
落在![]() 边上.
边上.
(2)求![]() 与
与![]() 的函数关系式.
的函数关系式.
(3)当直线![]() 将△
将△![]() 分为面积比为1:3的两部分时,直接写出
分为面积比为1:3的两部分时,直接写出![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com