【题目】两人要去某风景区游玩，每天某一时段开往该风景区有三辆汽车（票价相同），但是他们不知道这些车的舒适程度，也不知道汽车开过来的顺序．两人采用了不同的乘车方案：甲无论如何总是上开来的第一辆车．而乙则是先观察后上车，当第一辆车开来时，他不上车，而是仔细观察车的舒适状况．如果第二辆车的状况比第一辆好，他就上第二辆车；如果第二辆不比第一辆好，他就上第三辆车．如果把这三辆车的舒适程度分为上、中、下三等，请尝试解决下面的问题：请用树状图或列表法分析，甲、乙两人采用的方案，哪一种方案使自己乘坐上等车的可能性大．
【答案】乙采取的方案乘坐上等车的可能性大
【解析】
利用列举法展示所有6种等可能的结果；然后利用列表法展示甲乙乘车的所有结果，然后计算他们乘坐上等车的概率，再比较概率的大小．
解：三辆车开来的先后顺序有6种可能：
（上、中、下）、（上、下、中）、（中、上、下）、（中、下、上）、（下、中、上）、（下、上、中）；
由于不知道任何信息，所以只能假定6种顺序出现的可能性相同．我们来研究在各种可能性的顺序之下，甲、乙二人分别会上哪一辆汽车：
顺序 | 甲 | 乙 |
上、中、下 | 上 | 下 |
上、下、中 | 上 | 中 |
中、上、下 | 中 | 上 |
中、下、上 | 中 | 上 |
下、上、中 | 下 | 上 |
下、中、上 | 下 | 中 |
于是不难得出，甲乘上等车的概率是
；而乙乘上等车的概率是
．
∴乙采取的方案乘坐上等车的可能性大．
科目：初中数学 来源： 题型：
【题目】已知点A在x轴负半轴上，点B在y轴正半轴上，线段OB的长是方程x2﹣2x﹣8=0的解，tan∠BAO=
．
（1）求点A的坐标；
（2）点E在y轴负半轴上，直线EC⊥AB，交线段AB于点C，交x轴于点D，S△DOE=16．若反比例函数y=
的图象经过点C，求k的值；
（3）在（2）条件下，点M是DO中点，点N，P，Q在直线BD或y轴上，是否存在点P，使四边形MNPQ是矩形？若存在，请直接写出点P的坐标；若不存在，请说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
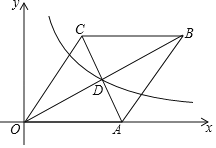
【题目】如图，在平面直角坐标系中，菱形OABC的边OA在x轴上，AC与OB交于点D （8，4），反比例函数y=
的图象经过点D．若将菱形OABC向左平移n个单位，使点C落在该反比例函数图象上，则n的值为 2 ．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知抛物线y＝x2+bx+c与x轴交于点A(4，﹣5)．
（1）如图，过点A分别向x轴、y轴作垂线，垂足分别为B、C，得到矩形ABOC，且抛物线经过点C．
①求抛物线的解析式．
②将抛物线沿直线x＝m（2＞m＞0）翻折，分别交线段OB、AC于D，E两点．若直线DE刚好平分矩形ABOC的面积，求m的值．
（2）将抛物线旋转180°，使点A的对应点为A1(m﹣2，n﹣4)，其中m≤2．若旋转后的抛物线仍然经过点A，求旋转后的抛物线顶点所能达到最低点时的坐标．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】我们将在直角坐标系中圆心坐标和半径均为整数的圆称为“整圆”．如图，直线l：y=kx+4
与x轴、y轴分别交于A、B，∠OAB=30°，点P在x轴上，⊙P与l相切，当P在线段OA上运动时，使得⊙P成为整圆的点P个数是（ ）
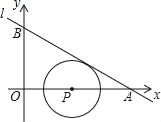
A. 6 B. 8 C. 10 D. 12
查看答案和解析>>
科目：初中数学 来源： 题型：
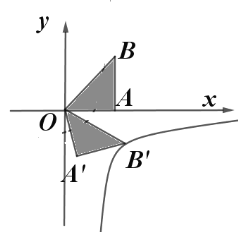
【题目】如图，等腰直角三角形
的直角顶点
在
轴的正半轴上，
，将
绕顶点
顺时针旋转
至
，使点
落在双曲线
的图象上，则
________，该双曲线的函数解析式为________．
查看答案和解析>>
科目：初中数学 来源： 题型：
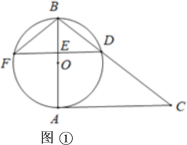
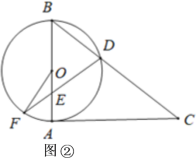
【题目】已知AB是⊙O的直径，AC是⊙O的切线，∠ABC=52°，BC交⊙O于点D，E是AB上一点，延长DE交⊙O于点F．
（Ⅰ）如图①，连接BF，求∠C和∠DFB的大小；
（Ⅱ）如图②，当DB=DE时，求∠OFD的大小．
查看答案和解析>>
科目：初中数学 来源： 题型：
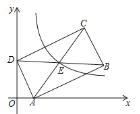
【题目】在平面直角坐标系中，矩形
的顶点
（1,0），
（0,2），点
在第一象限，
∥
轴，若函数
＝
的图象经过矩形的对角线的交点，则
的值为（ ）
A.4B.5C.8D.10
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
