
【题目】已知抛物线y=x2+bx+c与x轴交于点A(4,﹣5).
(1)如图,过点A分别向x轴、y轴作垂线,垂足分别为B、C,得到矩形ABOC,且抛物线经过点C.
①求抛物线的解析式.
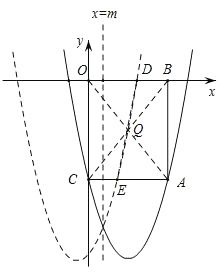
②将抛物线沿直线x=m(2>m>0)翻折,分别交线段OB、AC于D,E两点.若直线DE刚好平分矩形ABOC的面积,求m的值.
(2)将抛物线旋转180°,使点A的对应点为A1(m﹣2,n﹣4),其中m≤2.若旋转后的抛物线仍然经过点A,求旋转后的抛物线顶点所能达到最低点时的坐标.

【答案】(1)①y=x2﹣4x﹣5,②![]() ;(2)(2,﹣1)
;(2)(2,﹣1)
【解析】
(1)①由矩形的性质确定点C的坐标,将点C、A的坐标代入y=x2+bx+c即可求出抛物线的解析式;
②求出抛物线y=x2﹣4x﹣5的对称轴,求出翻折后的抛物线的对称轴,可写出翻折后的解析式,求出D,E两点坐标,因为直线DE刚好平分矩形ABOC的面积,则必过矩形对角线的交点Q(2,﹣![]() ),则可列出关于m的方程,即可求出m的值;
),则可列出关于m的方程,即可求出m的值;
(2)由点A、A1的坐标可求出旋转中心的坐标,进一步推出原顶点的对称点,可写出旋转后的抛物线解析式,因为旋转后的抛物线仍然经过点A,将点A的坐标代入旋转后的解析式,可得关于m、n的等式,将m=2代入,可求出n的值,即可写出旋转后的抛物线顶点所能达到最低点时的坐标.
解:(1)①∵点A(4,﹣5),且四边形ABOC为矩形,
∴C(0,﹣5),
∴抛物线的解析式为y=x2+bx﹣5,
将点A(4,﹣5)代入y=x2+bx﹣5,
得,b=﹣4,
∴抛物线的解析式为y=x2﹣4x﹣5;
②在抛物线y=x2﹣4x﹣5中,
对称轴为直线x=﹣![]() =2,
=2,
∵抛物线y=x2﹣4x﹣5沿直线x=m(2>m>0)翻折,
∴设翻折后的抛物线对称轴为直线x=n,
∴![]() =m,
=m,
∴n=2m﹣2,
∴翻折后的抛物线为y=[x﹣(2m﹣2)]2﹣9,
在y=[x﹣(2m﹣2)]2﹣9中,当y=0时,x1=2m+1,x2=2m﹣5;当y=﹣5时,x1=2m,x2=2m﹣4;
∵如下图,抛物线y=[x﹣(2m﹣2)]2﹣9分别交线段OB、AC于D,E两点,
∴D(2m+1,0),E(2m,﹣5),
∵直线DE刚好平分矩形ABOC的面积,
∴必过矩形对角线的交点Q(2,﹣![]() ),
),
即![]() =2,
=2,
∴m=![]() ;
;
(2)∵将抛物线旋转180°,使点A的对应点为A1(m﹣2,n﹣4),其中m≤2,
∵A(4,﹣5),
∴旋转中心为(![]() ,
,![]() ),
),
∴原顶点的对称点为(m,n),
∴旋转后的抛物线为y=﹣(x﹣m)2+n,
∵旋转后的抛物线仍然经过点A,
∴﹣5=﹣(4﹣m)2+n,
∵m≤2,
∴当m=2时,n=﹣1,
∵旋转后抛物线开口向下,
∴旋转后的抛物线顶点所能达到最低点时的坐标(2,﹣1).


科目:初中数学 来源: 题型:
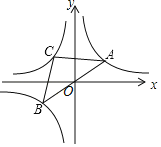
【题目】如图,已知A,B为反比例函数y1=![]() 图象上两点,连接AB,线段AB经过点O,C是反比例函数y2=
图象上两点,连接AB,线段AB经过点O,C是反比例函数y2=![]() (k<0)在第二象限内的图象上一点,当△CAB是以AB为底的等腰三角形,且
(k<0)在第二象限内的图象上一点,当△CAB是以AB为底的等腰三角形,且![]() 时,k的值为( )
时,k的值为( )
A.﹣![]() B.﹣3C.﹣4D.﹣
B.﹣3C.﹣4D.﹣![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在![]() 中,
中,![]() ,点
,点![]() 分别是边
分别是边![]() 的中点,连接
的中点,连接![]() ,
,
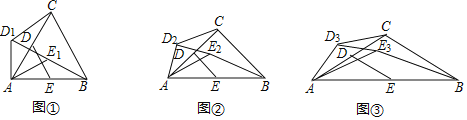
(1)如图①,当![]() 时,
时,![]() 绕点
绕点![]() 逆时针旋转得到
逆时针旋转得到![]() ,连接
,连接![]() 、
、![]() ,
,![]() 在旋转过程中请猜想:
在旋转过程中请猜想:![]() ______(直接写出答案);
______(直接写出答案);
(2)如图②,当![]() 时,
时,![]() 绕点
绕点![]() 逆时针旋转得到
逆时针旋转得到![]() ,连接
,连接![]() 、
、![]() ,
,![]() 在旋转过程中请猜想:
在旋转过程中请猜想:![]() 的比值,并证明你的猜想;
的比值,并证明你的猜想;
(3)如图③,当![]() 时,
时,![]() 绕点
绕点![]() 逆时针旋转得到
逆时针旋转得到![]() ,连接
,连接![]() 、
、![]() ,请直接写出
,请直接写出![]() 在旋转过程中
在旋转过程中![]() 的比值.(用含
的比值.(用含![]() 的代数式表示)
的代数式表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中华文明,源远流长,中华汉字,寓意深广.为传承中华优秀传统文化,某中学德育处组织了一次全校2000名学生参加的“汉字听写”大赛.为了解本次大赛的成绩,学校德育处随机抽取了其中200名学生的成绩作为样本进行统计,制成如下不完整的统计图表:
成绩x(分)分数段 | 频数(人) | 频率 |
50≤x<60 | 10 | 0.05 |
60≤x<70 | 30 | 0.15 |
70≤x<80 | 40 | 0.2 |
80≤x<90 | m | 0.35 |
90≤x<100 | 50 | n |
频数分布直方图
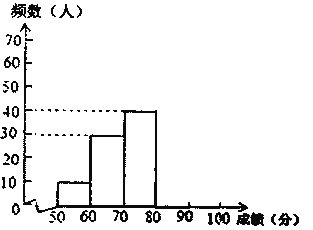
根据所给的信息,回答下列问题:
(1)m=________;n=________;
(2)补全频数分布直方图;
(3)这200名学生成绩的中位数会落在________分数段;
(4)若成绩在90分以上(包括90分)为“优”等,请你估计该校参加本次比赛的2000名学生中成绩是“优”等的约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(3分)如图,在直角坐标系中,直线![]() 与坐标轴交于A、B两点,与双曲线
与坐标轴交于A、B两点,与双曲线![]() (
(![]() )交于点C,过点C作CD⊥x轴,垂足为D,且OA=AD,则以下结论:
)交于点C,过点C作CD⊥x轴,垂足为D,且OA=AD,则以下结论:
①![]() ;
;
②当0<x<3时,![]() ;
;
③如图,当x=3时,EF=![]() ;
;
④当x>0时,![]() 随x的增大而增大,
随x的增大而增大,![]() 随x的增大而减小.
随x的增大而减小.
其中正确结论的个数是( )
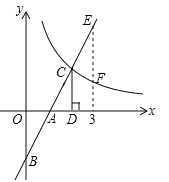
A.1 B.2 C.3 D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】两人要去某风景区游玩,每天某一时段开往该风景区有三辆汽车(票价相同),但是他们不知道这些车的舒适程度,也不知道汽车开过来的顺序.两人采用了不同的乘车方案:甲无论如何总是上开来的第一辆车.而乙则是先观察后上车,当第一辆车开来时,他不上车,而是仔细观察车的舒适状况.如果第二辆车的状况比第一辆好,他就上第二辆车;如果第二辆不比第一辆好,他就上第三辆车.如果把这三辆车的舒适程度分为上、中、下三等,请尝试解决下面的问题:请用树状图或列表法分析,甲、乙两人采用的方案,哪一种方案使自己乘坐上等车的可能性大.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某种蔬菜的销售单价y1与销售月份x之间的关系如图1所示,成本y2与销售月份x之间的关系如图2所示(图1的图象是线段,图2的图象是抛物线)
(1)已知6月份这种蔬菜的成本最低,此时出售每千克的收益是多少元?(收益=售价﹣成本)
(2)哪个月出售这种蔬菜,每千克的收益最大?简单说明理由.
(3)已知市场部销售该种蔬菜4、5两个月的总收益为22万元,且5月份的销售量比4月份的销售量多2万千克,求4、5两个月的销售量分别是多少万千克?
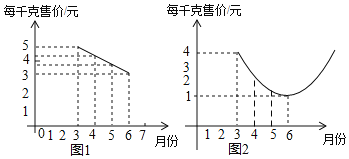
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】教材呈现:下图是华师版八年级下册数学教材第11页的部分内容.
例1,如图,在菱形![]() 中,
中,![]() ,试求
,试求![]() 的大小,并说明
的大小,并说明![]() 是等边三角形
是等边三角形
问题解决:请结合图(1),写出例1的完整解答过程;

问题探究:在菱形![]() 中,对角线
中,对角线![]() 相交于点
相交于点![]() ,过点D作
,过点D作![]() 交BC的延长线于点E.
交BC的延长线于点E.
(1)如图2,连接OE,则OE的长为____________;
(2)如图3,若点P是对角线BD上一动点,连结![]() ,则
,则![]() 的最小值为____________.
的最小值为____________.
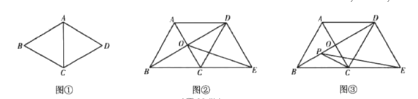
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com