
【题目】如图,在![]() 中,
中,![]() ,
,![]() 平分
平分![]() 交
交![]() 于点
于点![]() ,将
,将![]() 绕点
绕点![]() 顺时针旋转到
顺时针旋转到![]() 的位置,点
的位置,点![]() 在
在![]() 上.
上.
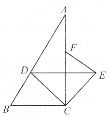
(1)![]() 旋转的度数为______
旋转的度数为______![]() ;
;
(2)连结![]() ,判断
,判断![]() 与
与![]() 的位置关系,并说明理由.
的位置关系,并说明理由.
科目:初中数学 来源: 题型:
【题目】某公司计划6月底组织员工到某地旅游,参加旅游的人数估计为5-20人,甲、乙两家旅行社的服务质量相同,且报价都是每人200元.经过协商,甲旅行社表示可给予每位游客七折优惠;乙旅行社表示可先免去一位游客的旅游费用,其余游客八折优惠.请你帮他们算一算该公司应选择哪一家旅行社支付的旅游费用较少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点A在x轴负半轴上,点B在y轴正半轴上,线段OB的长是方程x2﹣2x﹣8=0的解,tan∠BAO=![]() .
.
(1)求点A的坐标;
(2)点E在y轴负半轴上,直线EC⊥AB,交线段AB于点C,交x轴于点D,S△DOE=16.若反比例函数y=![]() 的图象经过点C,求k的值;
的图象经过点C,求k的值;
(3)在(2)条件下,点M是DO中点,点N,P,Q在直线BD或y轴上,是否存在点P,使四边形MNPQ是矩形?若存在,请直接写出点P的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
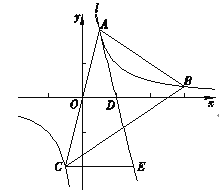
【题目】如图,在平面直角坐标系xOy中,点![]() ,
, ![]() 在反比例函数
在反比例函数![]() (m为常数)的图象上,连接AO并延长与图象的另一支有另一个交点为点C,过点A的直线l与x轴的交点为点
(m为常数)的图象上,连接AO并延长与图象的另一支有另一个交点为点C,过点A的直线l与x轴的交点为点![]() ,过点C作CE∥x轴交直线l于点E.
,过点C作CE∥x轴交直线l于点E.
(1)求m的值,并求直线l对应的函数解析式;
(2)求点E的坐标;
(3)过点B作射线BN∥x轴,与AE交于点M (补全图形),求证: ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某印刷厂的打印机每5年需淘汰一批旧打印机并购买新机,买新机时,同时购买墨盒,每盒150元,每台新机最多可配买24盒;若非同时配买,则每盒需220元.
公司根据以往的记录,十台打印机正常工作五年消耗墨盒数如表:
消耗墨盒数 | 22 | 23 | 24 | 25 |
打印机台数 | 1 | 4 | 4 | 1 |
(1)以这十台打印机消耗墨盒数为样本,估计“一年该款打印机正常工作5年消耗的墨盒数不大于24”的概率;
(2)试以这10台打印机5年消耗的墨盒数的平均数作为决策依据,说明购买10台该款打印机时,每台应统一配买23盒墨还是24盒墨更合算?
查看答案和解析>>
科目:初中数学 来源: 题型:
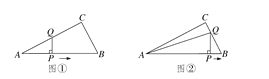
【题目】如图,在△ABC中,∠ACB=90°,AB=10,tanA=![]() .点P是斜边AB上一个动点,过点P作PQ⊥AB,垂足为P,交边AC(或边CB)于点Q.设AP=x,△APQ的面积为y,则y与x之间的函数图象大致为( )
.点P是斜边AB上一个动点,过点P作PQ⊥AB,垂足为P,交边AC(或边CB)于点Q.设AP=x,△APQ的面积为y,则y与x之间的函数图象大致为( )
A.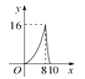
B.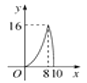
C.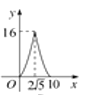
D.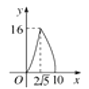
查看答案和解析>>
科目:初中数学 来源: 题型:
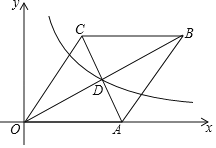
【题目】如图,在平面直角坐标系中,菱形OABC的边OA在x轴上,AC与OB交于点D (8,4),反比例函数y=![]() 的图象经过点D.若将菱形OABC向左平移n个单位,使点C落在该反比例函数图象上,则n的值为 2 .
的图象经过点D.若将菱形OABC向左平移n个单位,使点C落在该反比例函数图象上,则n的值为 2 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=x2+bx+c与x轴交于点A(4,﹣5).
(1)如图,过点A分别向x轴、y轴作垂线,垂足分别为B、C,得到矩形ABOC,且抛物线经过点C.
①求抛物线的解析式.
②将抛物线沿直线x=m(2>m>0)翻折,分别交线段OB、AC于D,E两点.若直线DE刚好平分矩形ABOC的面积,求m的值.
(2)将抛物线旋转180°,使点A的对应点为A1(m﹣2,n﹣4),其中m≤2.若旋转后的抛物线仍然经过点A,求旋转后的抛物线顶点所能达到最低点时的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
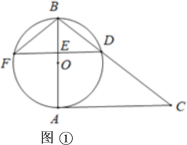
【题目】已知AB是⊙O的直径,AC是⊙O的切线,∠ABC=52°,BC交⊙O于点D,E是AB上一点,延长DE交⊙O于点F.
(Ⅰ)如图①,连接BF,求∠C和∠DFB的大小;
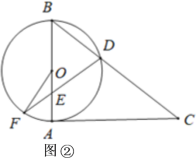
(Ⅱ)如图②,当DB=DE时,求∠OFD的大小.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com