
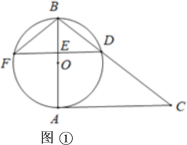
【题目】已知AB是⊙O的直径,AC是⊙O的切线,∠ABC=52°,BC交⊙O于点D,E是AB上一点,延长DE交⊙O于点F.
(Ⅰ)如图①,连接BF,求∠C和∠DFB的大小;
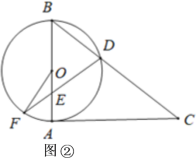
(Ⅱ)如图②,当DB=DE时,求∠OFD的大小.
【答案】(Ⅰ)∠C=38°;∠DFB=38°;(Ⅱ)∠F=24°.
【解析】
(1)连接AD,利用切线的性质得出∠BAC=90°,从而得出∠C的度数;利用![]() 是⊙
是⊙![]() 的直径,得∠ADB=90°,从而得出∠DAB的度数,进而得出
的直径,得∠ADB=90°,从而得出∠DAB的度数,进而得出![]() 的度数;
的度数;
(2)连接OD,利用∠BED=∠B =52°,得出∠BDE的度数,利用OB=OD得出∠BDO的度数,从而得出∠ODF的度数,进而得出∠F的度数.
解:(Ⅰ)如图,连接AD.
∵ AC是⊙![]() 的切线,
的切线,![]() 是⊙
是⊙![]() 的直径,
的直径,
∴ AB⊥AC,即∠BAC=90°.
∵∠ABC=52° ,
∴∠C=90°-∠ABC=90°-52°=38°.
由![]() 是⊙
是⊙![]() 的直径,得∠ADB=90°.
的直径,得∠ADB=90°.
∴∠DAB=90°-∠ABC=90°-52°=38°.
∵![]()
∴![]() =∠DAB=38°.
=∠DAB=38°.
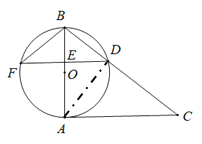
(Ⅱ)如图,连接OD.
在△BDE中,DB=DE,∠B=52°,
∴∠BED=∠B =52°,
∴∠BDE=180°-∠BED-∠B=76°.
又在△BOD中,OB=OD,∴∠BDO=∠B=52°,
∴ ∠ODF=76°-52°=24°.
∵ OD=OF,
∴∠F=∠ODF=24°.


科目:初中数学 来源: 题型:
【题目】两人要去某风景区游玩,每天某一时段开往该风景区有三辆汽车(票价相同),但是他们不知道这些车的舒适程度,也不知道汽车开过来的顺序.两人采用了不同的乘车方案:甲无论如何总是上开来的第一辆车.而乙则是先观察后上车,当第一辆车开来时,他不上车,而是仔细观察车的舒适状况.如果第二辆车的状况比第一辆好,他就上第二辆车;如果第二辆不比第一辆好,他就上第三辆车.如果把这三辆车的舒适程度分为上、中、下三等,请尝试解决下面的问题:请用树状图或列表法分析,甲、乙两人采用的方案,哪一种方案使自己乘坐上等车的可能性大.
查看答案和解析>>
科目:初中数学 来源: 题型:
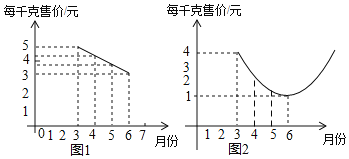
【题目】某种蔬菜的销售单价y1与销售月份x之间的关系如图1所示,成本y2与销售月份x之间的关系如图2所示(图1的图象是线段,图2的图象是抛物线)
(1)已知6月份这种蔬菜的成本最低,此时出售每千克的收益是多少元?(收益=售价﹣成本)
(2)哪个月出售这种蔬菜,每千克的收益最大?简单说明理由.
(3)已知市场部销售该种蔬菜4、5两个月的总收益为22万元,且5月份的销售量比4月份的销售量多2万千克,求4、5两个月的销售量分别是多少万千克?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() .点
.点![]() 从点
从点![]() 出发,以每秒3个单位长度的速度向终点
出发,以每秒3个单位长度的速度向终点![]() 运动,过点
运动,过点![]() 作
作![]() 交
交![]() 边或
边或![]() 边于点
边于点![]() ,点
,点![]() 是射线
是射线![]() 边上一点,总保持
边上一点,总保持![]() ,以
,以![]() 、
、![]() 为邻边构造矩形
为邻边构造矩形![]() ,设矩形
,设矩形![]() 与
与![]() 重叠部分图形的面积为
重叠部分图形的面积为![]() ,点
,点![]() 的运动时间为
的运动时间为![]() .
.
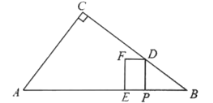
(1)用含![]() 的式子表示线段
的式子表示线段![]() 的长;
的长;
(2)当点![]() 落在
落在![]() 上时,求
上时,求![]() 的值;
的值;
(3)当矩形![]() 与
与![]() 重叠部分图形为四边形时,求
重叠部分图形为四边形时,求![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(4)点![]() 与点
与点![]() 同时出发,在线段
同时出发,在线段![]() 上以每秒5个单位长度的速度沿
上以每秒5个单位长度的速度沿![]() 往返一次,连结
往返一次,连结![]() 、
、![]() ,直接写出矩形
,直接写出矩形![]() 的面积是
的面积是![]() 的面积的2倍时
的面积的2倍时![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某汽车专卖店销售A、B两种型号的新能源汽车.上周售出1辆A型车和3辆B型车,两种车型的销售总额为96万元;本周销售2辆A型车和1辆B型车,两种车型的销售总额为62万元,已知两种型号汽车销售价格始终不变.
(1)求A、B两种车型的销售单价分别是多少?
(2)第三周计划售出A、B两种型号的车共5辆,若销售总额不少于100万元,则B型车至少要售出多少辆?
查看答案和解析>>
科目:初中数学 来源: 题型:
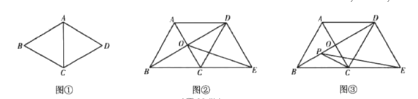
【题目】教材呈现:下图是华师版八年级下册数学教材第11页的部分内容.
例1,如图,在菱形![]() 中,
中,![]() ,试求
,试求![]() 的大小,并说明
的大小,并说明![]() 是等边三角形
是等边三角形
问题解决:请结合图(1),写出例1的完整解答过程;

问题探究:在菱形![]() 中,对角线
中,对角线![]() 相交于点
相交于点![]() ,过点D作
,过点D作![]() 交BC的延长线于点E.
交BC的延长线于点E.
(1)如图2,连接OE,则OE的长为____________;
(2)如图3,若点P是对角线BD上一动点,连结![]() ,则
,则![]() 的最小值为____________.
的最小值为____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某小微企业为加快产业转型升级步伐,引进一批A,B两种型号的机器.已知一台A型机器比一台B型机器每小时多加工2个零件,且一台A型机器加工80个零件与一台B型机器加工60个零件所用时间相等.
(1)每台A,B两种型号的机器每小时分别加工多少个零件?
(2)如果该企业计划安排A,B两种型号的机器共10台一起加工一批该零件,为了如期完成任务,要求两种机器每小时加工的零件不少于72件,同时为了保障机器的正常运转,两种机器每小时加工的零件不能超过76件,那么A,B两种型号的机器可以各安排多少台?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com