【题目】某汽车专卖店销售A、B两种型号的新能源汽车．上周售出1辆A型车和3辆B型车，两种车型的销售总额为96万元；本周销售2辆A型车和1辆B型车，两种车型的销售总额为62万元，已知两种型号汽车销售价格始终不变．
（1）求A、B两种车型的销售单价分别是多少？
（2）第三周计划售出A、B两种型号的车共5辆，若销售总额不少于100万元，则B型车至少要售出多少辆？
【答案】（1）每辆A型车售价为18万元，B型车的售价为26万元；（2）B型车至少售出2辆
【解析】
（1）设每辆A型车售价为x万元，B型车的售价为y万元，根据“上周售出1辆A型车和3辆B型车，两种车型的销售总额为96万元；本周销售2辆A型车和1辆B型车，两种车型的销售总额为62万元”可列出关于x、y的二元一次方程组求解即可；
（2）设第三周计划售出B型车m辆，则A型车售出
辆，再根据“若销售总额不少于100万元”列出不等式求解即可.
解：（1）设每辆A型车售价为x万元，B型车的售价为y万元，
根据题意，得
，
解得：
，
答：每辆A型车售价为18万元，B型车的售价为26万元．
（2）设第三周计划售出B型车m辆，则A型车售出辆，
根据题意，得：
解得：
答：B型车至少售出2辆．
科目：初中数学 来源： 题型：
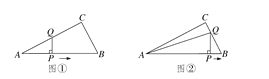
【题目】如图，在△ABC中，∠ACB＝90°，AB＝10，tanA＝
.点P是斜边AB上一个动点，过点P作PQ⊥AB，垂足为P，交边AC(或边CB)于点Q.设AP＝x，△APQ的面积为y，则y与x之间的函数图象大致为( )
A.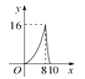
B.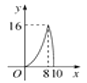
C.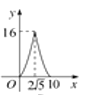
D.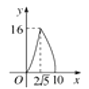
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】小玲和弟弟小东分别从家和图书馆同时出发，沿同一条路相向而行，小玲开始跑步中途改为步行，到达图书馆恰好用30min．小东骑自行车以300m/min的速度直接回家，两人离家的路程y（m）与各自离开出发地的时间x（min）之间的函数图象如图所示
（1）家与图书馆之间的路程为多少m，小玲步行的速度为多少m/min；
（2）求小东离家的路程y关于x的函数解析式，并写出自变量的取值范围；
（3）求两人相遇的时间．
查看答案和解析>>
科目：初中数学 来源： 题型：
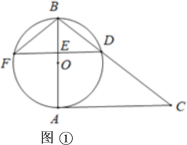
【题目】已知AB是⊙O的直径，AC是⊙O的切线，∠ABC=52°，BC交⊙O于点D，E是AB上一点，延长DE交⊙O于点F．
（Ⅰ）如图①，连接BF，求∠C和∠DFB的大小；
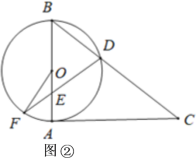
（Ⅱ）如图②，当DB=DE时，求∠OFD的大小．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图1，抛物线
与x轴交于A、B两点，与y轴交于C点，连接
、
，已知点A、C的坐标为
、
．
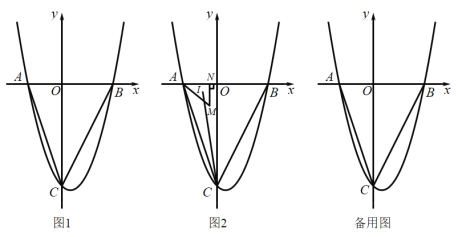
（1）求抛物线的表达式；
（2）点P是线段下方抛物线上的一动点，如果在x轴上存在点Q，使得以点B、C、P、Q为顶点的四边形为平行四边形，求点Q的坐标；
（3）如图2，若点M是
内一动点，且满足
，过点M作
，垂足为N，设
的内心为I，试求
的最小值．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图①，在矩形ABCD中，AB＝6，BC＝9，点E是BC边上一动点，连接AE、DE ，作△ECD的外接⊙O，交AD于点F，交AE于点G，连接FG．
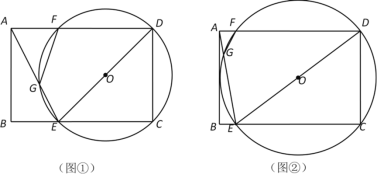
（1）求证△AFG∽△AED；
（2）当BE的长为 时，△AFG为等腰三角形；
（3）如图②，若BE＝1，求证：AB与⊙O相切．
查看答案和解析>>
科目：初中数学 来源： 题型：
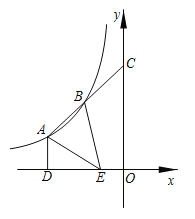
【题目】如图，A，B是反比例函数
(k≠0)图象上的两点，延长线段AB交y轴于点C，且B为线段AC的中点，过点A作AD⊥x轴于点D，E为线段OD的三等分点，且OE＜DE．连接AE，BE．若S△ABE＝7，则k的值为_________．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】甲、乙、丙、丁四人做传球游戏：第一次由甲将球随机传给乙、丙、丁中的某一人，第二次由持球者将球再随机传给其他三人中的某一人．
（1）第一次传球后球到乙手里的概率为 ；
（2）画树状图或列表求第二次传球后球回到甲手里的概率．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
