
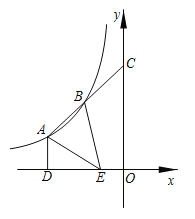
【题目】如图,A,B是反比例函数![]() (k≠0)图象上的两点,延长线段AB交y轴于点C,且B为线段AC的中点,过点A作AD⊥x轴于点D,E为线段OD的三等分点,且OE<DE.连接AE,BE.若S△ABE=7,则k的值为_________.
(k≠0)图象上的两点,延长线段AB交y轴于点C,且B为线段AC的中点,过点A作AD⊥x轴于点D,E为线段OD的三等分点,且OE<DE.连接AE,BE.若S△ABE=7,则k的值为_________.
【答案】-12
【解析】
设A(m,![]() ),C(0,n),则D(m,0),E(
),C(0,n),则D(m,0),E(![]() m,0),由AB=BC,推出B(
m,0),由AB=BC,推出B(![]() ,
,![]() ),根据点B在
),根据点B在![]() 上,求出mn=3k,连接EC,OA,因为AB=BC,推出S△AEC=2S△AEB=14,根据S△AEC=S△AEO+S△ACO-S△ECO,构建方程即可解决问题;
上,求出mn=3k,连接EC,OA,因为AB=BC,推出S△AEC=2S△AEB=14,根据S△AEC=S△AEO+S△ACO-S△ECO,构建方程即可解决问题;
解:设A(m,![]() ),C(0,n),则D(m,0),E(
),C(0,n),则D(m,0),E(![]() m,0),
m,0),
∵B为AC的中点,
∴AB=BC,
∴B(![]() ,
,![]() ),
),
∵点B在反比例函数![]() (k≠0)的图象上,
(k≠0)的图象上,
∴
∴k+mn=4k,
∴mn=3k,
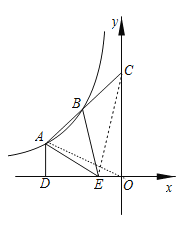
如图,连接EC,OA,
∵AB=BC,
∴S△AEC=2S△AEB=14,
∵S△AEC=S△AEO+S△ACO-S△ECO,
∴14=![]() ,
,
∴14=![]() ,
,
∴k=-12.


科目:初中数学 来源: 题型:
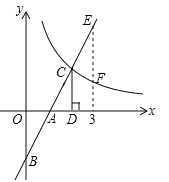
【题目】(3分)如图,在直角坐标系中,直线![]() 与坐标轴交于A、B两点,与双曲线
与坐标轴交于A、B两点,与双曲线![]() (
(![]() )交于点C,过点C作CD⊥x轴,垂足为D,且OA=AD,则以下结论:
)交于点C,过点C作CD⊥x轴,垂足为D,且OA=AD,则以下结论:
①![]() ;
;
②当0<x<3时,![]() ;
;
③如图,当x=3时,EF=![]() ;
;
④当x>0时,![]() 随x的增大而增大,
随x的增大而增大,![]() 随x的增大而减小.
随x的增大而减小.
其中正确结论的个数是( )
A.1 B.2 C.3 D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某汽车专卖店销售A、B两种型号的新能源汽车.上周售出1辆A型车和3辆B型车,两种车型的销售总额为96万元;本周销售2辆A型车和1辆B型车,两种车型的销售总额为62万元,已知两种型号汽车销售价格始终不变.
(1)求A、B两种车型的销售单价分别是多少?
(2)第三周计划售出A、B两种型号的车共5辆,若销售总额不少于100万元,则B型车至少要售出多少辆?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2020年的春节,对于我们来说,有些不一样,我们不能和小伙伴相约一起玩耍,不能去游乐场放飞自我,也不能和自己的兄弟姐妹一起吃美味的大餐,这么做,是因为我们每一个人都在面临一个眼睛看不到的敌人,它叫病毒,残酷的病毒会让人患上肺炎,人与人的接触会让这种疾病快速地传播开来,严重的还会有生命危险,目前我省已经启动突发公共卫生事件一级应急响应,但我们相信,只要大家一起努力,疫情终有会被战胜的一天.
在这个不能出门的悠长假期里,某小学随机对本校部分学生进行“假期中,我在家可以这么做!A.扎实学习、B.快乐游戏、C.经典阅读、D.分担劳动、E.乐享健康”的网络调查,并根据调查结果绘制成如下两幅不完整的统计图(若每一位同学只能选择一项),请根据图中的信息,回答下列问题.
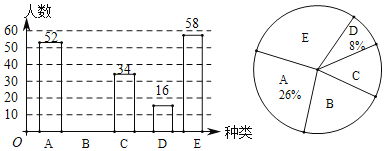
(1)这次调查的总人数是 人;
(2)请补全条形统计图,并说明扇形统计图中E所对应的圆心角是 度;
(3)若学校共有学生的1700人,则选择C有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
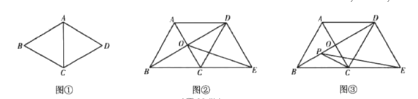
【题目】教材呈现:下图是华师版八年级下册数学教材第11页的部分内容.
例1,如图,在菱形![]() 中,
中,![]() ,试求
,试求![]() 的大小,并说明
的大小,并说明![]() 是等边三角形
是等边三角形
问题解决:请结合图(1),写出例1的完整解答过程;

问题探究:在菱形![]() 中,对角线
中,对角线![]() 相交于点
相交于点![]() ,过点D作
,过点D作![]() 交BC的延长线于点E.
交BC的延长线于点E.
(1)如图2,连接OE,则OE的长为____________;
(2)如图3,若点P是对角线BD上一动点,连结![]() ,则
,则![]() 的最小值为____________.
的最小值为____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
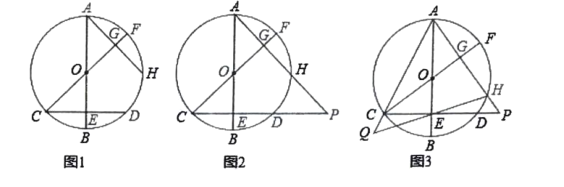
【题目】已知:![]() 都是
都是![]() 的直径,
的直径,![]() 都是
都是![]() 的弦,
的弦,![]() 于点
于点![]() ,
,![]() .
.
(1)如图1,求证:![]() ;
;
(2)如图2,延长![]() 交于点
交于点![]() ,求证:
,求证:![]() ;
;
(3)如图3,在(2)的条件下,延长![]() ,
,![]() 交于点
交于点![]() ,若
,若![]() ,
,![]() ,求
,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△![]() 中,高
中,高![]() =3,∠
=3,∠![]() =45°,
=45°,![]() =
=![]() ,动点
,动点![]() 从点
从点![]() 出发,沿
出发,沿![]() 方向以每秒1个单位长度的速速向终点
方向以每秒1个单位长度的速速向终点![]() 运动,当点
运动,当点![]() 与点
与点![]() 、
、![]() 不重合时,过点
不重合时,过点![]() 作
作![]() 、
、![]() 的平行线,与
的平行线,与![]() 分别交于点
分别交于点![]() 、
、![]() ,将△
,将△![]() 绕
绕![]() 的中点旋转180°得△
的中点旋转180°得△![]() ,设点
,设点![]() 的运动时间为
的运动时间为![]() 秒,△
秒,△![]() 与△
与△![]() 重叠部分面积为
重叠部分面积为![]() .
.
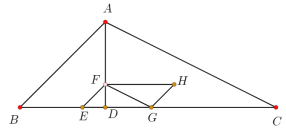
(1)当![]() = 秒时,点
= 秒时,点![]() 落在
落在![]() 边上.
边上.
(2)求![]() 与
与![]() 的函数关系式.
的函数关系式.
(3)当直线![]() 将△
将△![]() 分为面积比为1:3的两部分时,直接写出
分为面积比为1:3的两部分时,直接写出![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
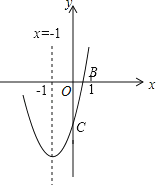
【题目】已知二次函数y=ax2+bx+c(a≠0)的对称轴为直线x=﹣1,与x轴的一个交点B的坐标为(1,0)其图象如图所示,下列结论:①abc>0;②2a﹣b=0;③一元二次方程ax2+bx+c=0的两个根是﹣3和1;④当y>0时,﹣3<x<1;⑤当x>0时,y随x的增大而增大:⑥若点E(﹣4,y1),F(﹣2,y2),M(3,y3)是函数图象上的三点,则y1>y2>y3,其中正确的有( )个
A.5B.4C.3D.2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点A(﹣3,y1),B(2,y2)均在抛物线y=ax2+bx+c上,点P(m,n)是该抛物线的顶点,若y1>y2≥n,则m的取值范围是( )
A.﹣3<m<2B.﹣![]() <m<-
<m<-![]() C.m>﹣
C.m>﹣![]() D.m>2
D.m>2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com