
【题目】如图①,在矩形ABCD中,AB=6,BC=9,点E是BC边上一动点,连接AE、DE ,作△ECD的外接⊙O,交AD于点F,交AE于点G,连接FG.
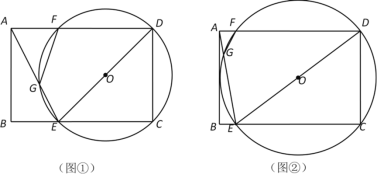
(1)求证△AFG∽△AED;
(2)当BE的长为 时,△AFG为等腰三角形;
(3)如图②,若BE=1,求证:AB与⊙O相切.
【答案】(1)详见解析;(2)3![]() 、4.5、9-3
、4.5、9-3![]() ;(3)详见解析
;(3)详见解析
【解析】
(1)根据圆内接四边形的性质可得∠AGF=∠ADE,又∠GAF=∠DAE,从而可证明△AFG∽△AED;
(2)先证明四边形ABEF是矩形,得EF=6,然后分当![]() 时;当
时;当![]() 时;当
时;当![]() 时三种情况,运用勾股定理求解即可;
时三种情况,运用勾股定理求解即可;
(3)连接OM,运用梯形中位线证明OM=OD,![]() 即可.
即可.
(1)证明:∵四边形FGED是⊙O的内接四边形,
∴∠AGF=∠ADE.
又∠GAF=∠DAE,
∴△AFG∽△AED;
(2)由(1)可知△AFG∽△AED,
∴当△AFG是等腰三角形时,△AED是等腰三角形时,
连接EF,如图,
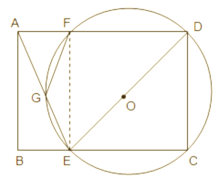
∵四边形ABCD是矩形,![]() ,
,![]()
![]() ,
,![]() ,
,![]()
![]() ,
,
![]() 是
是![]() 的外接圆,
的外接圆,![]()
![]() 是
是![]() 的直径,
的直径,
![]() ,
,
![]() ,
,
![]() ,
,
∴四边形![]() 是矩形,
是矩形,
![]() ,
,
![]() 是等腰三角形,
是等腰三角形,
∴分三种情况:
①当![]() 时,
时,![]() ,
,
![]() ,
,
又![]() ,
,
![]() ,
,
![]() ;
;
②当![]() 时,
时,
在![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,
![]()
![]() ,
,
![]() ;
;
③当![]() 时
时
在![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,
![]()
![]()
综上,当![]() 的长为
的长为![]() 或
或![]() 或
或![]() 时,
时,![]() 为等腰三角形,
为等腰三角形,
(3)设AB的中点为M,连接OM,如图,
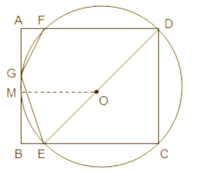
当![]() 时,
时,![]() ,
,
∵四边形![]() 是矩形,
是矩形,
![]() ,
,![]() ,
,![]() ,
,
在![]() 中,
中,![]() ,
,
![]()
![]() 是
是![]() 的直径,
的直径,
![]()
![]() ,
,
∴四边形![]() 是梯形,
是梯形,
又![]() 是AB的中点,O为DE的中点,
是AB的中点,O为DE的中点,
![]() 是梯形
是梯形![]() 的中位线,
的中位线,
![]()
![]() ,
,
![]() ,
,![]()
![]()
又![]()
∴AB与![]() 相切.
相切.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】在![]() 中,
中,![]() ,点
,点![]() 分别是边
分别是边![]() 的中点,连接
的中点,连接![]() ,
,
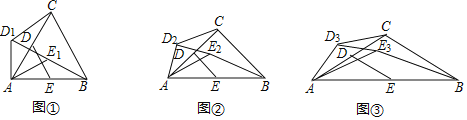
(1)如图①,当![]() 时,
时,![]() 绕点
绕点![]() 逆时针旋转得到
逆时针旋转得到![]() ,连接
,连接![]() 、
、![]() ,
,![]() 在旋转过程中请猜想:
在旋转过程中请猜想:![]() ______(直接写出答案);
______(直接写出答案);
(2)如图②,当![]() 时,
时,![]() 绕点
绕点![]() 逆时针旋转得到
逆时针旋转得到![]() ,连接
,连接![]() 、
、![]() ,
,![]() 在旋转过程中请猜想:
在旋转过程中请猜想:![]() 的比值,并证明你的猜想;
的比值,并证明你的猜想;
(3)如图③,当![]() 时,
时,![]() 绕点
绕点![]() 逆时针旋转得到
逆时针旋转得到![]() ,连接
,连接![]() 、
、![]() ,请直接写出
,请直接写出![]() 在旋转过程中
在旋转过程中![]() 的比值.(用含
的比值.(用含![]() 的代数式表示)
的代数式表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
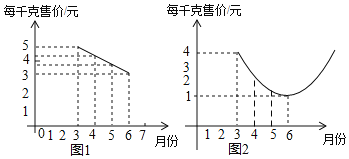
【题目】某种蔬菜的销售单价y1与销售月份x之间的关系如图1所示,成本y2与销售月份x之间的关系如图2所示(图1的图象是线段,图2的图象是抛物线)
(1)已知6月份这种蔬菜的成本最低,此时出售每千克的收益是多少元?(收益=售价﹣成本)
(2)哪个月出售这种蔬菜,每千克的收益最大?简单说明理由.
(3)已知市场部销售该种蔬菜4、5两个月的总收益为22万元,且5月份的销售量比4月份的销售量多2万千克,求4、5两个月的销售量分别是多少万千克?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某汽车专卖店销售A、B两种型号的新能源汽车.上周售出1辆A型车和3辆B型车,两种车型的销售总额为96万元;本周销售2辆A型车和1辆B型车,两种车型的销售总额为62万元,已知两种型号汽车销售价格始终不变.
(1)求A、B两种车型的销售单价分别是多少?
(2)第三周计划售出A、B两种型号的车共5辆,若销售总额不少于100万元,则B型车至少要售出多少辆?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2020年的春节,对于我们来说,有些不一样,我们不能和小伙伴相约一起玩耍,不能去游乐场放飞自我,也不能和自己的兄弟姐妹一起吃美味的大餐,这么做,是因为我们每一个人都在面临一个眼睛看不到的敌人,它叫病毒,残酷的病毒会让人患上肺炎,人与人的接触会让这种疾病快速地传播开来,严重的还会有生命危险,目前我省已经启动突发公共卫生事件一级应急响应,但我们相信,只要大家一起努力,疫情终有会被战胜的一天.
在这个不能出门的悠长假期里,某小学随机对本校部分学生进行“假期中,我在家可以这么做!A.扎实学习、B.快乐游戏、C.经典阅读、D.分担劳动、E.乐享健康”的网络调查,并根据调查结果绘制成如下两幅不完整的统计图(若每一位同学只能选择一项),请根据图中的信息,回答下列问题.
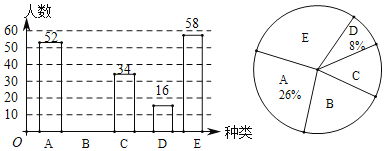
(1)这次调查的总人数是 人;
(2)请补全条形统计图,并说明扇形统计图中E所对应的圆心角是 度;
(3)若学校共有学生的1700人,则选择C有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
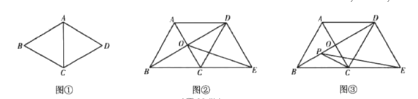
【题目】教材呈现:下图是华师版八年级下册数学教材第11页的部分内容.
例1,如图,在菱形![]() 中,
中,![]() ,试求
,试求![]() 的大小,并说明
的大小,并说明![]() 是等边三角形
是等边三角形
问题解决:请结合图(1),写出例1的完整解答过程;

问题探究:在菱形![]() 中,对角线
中,对角线![]() 相交于点
相交于点![]() ,过点D作
,过点D作![]() 交BC的延长线于点E.
交BC的延长线于点E.
(1)如图2,连接OE,则OE的长为____________;
(2)如图3,若点P是对角线BD上一动点,连结![]() ,则
,则![]() 的最小值为____________.
的最小值为____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△![]() 中,高
中,高![]() =3,∠
=3,∠![]() =45°,
=45°,![]() =
=![]() ,动点
,动点![]() 从点
从点![]() 出发,沿
出发,沿![]() 方向以每秒1个单位长度的速速向终点
方向以每秒1个单位长度的速速向终点![]() 运动,当点
运动,当点![]() 与点
与点![]() 、
、![]() 不重合时,过点
不重合时,过点![]() 作
作![]() 、
、![]() 的平行线,与
的平行线,与![]() 分别交于点
分别交于点![]() 、
、![]() ,将△
,将△![]() 绕
绕![]() 的中点旋转180°得△
的中点旋转180°得△![]() ,设点
,设点![]() 的运动时间为
的运动时间为![]() 秒,△
秒,△![]() 与△
与△![]() 重叠部分面积为
重叠部分面积为![]() .
.
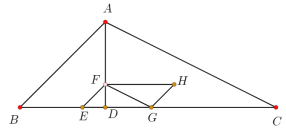
(1)当![]() = 秒时,点
= 秒时,点![]() 落在
落在![]() 边上.
边上.
(2)求![]() 与
与![]() 的函数关系式.
的函数关系式.
(3)当直线![]() 将△
将△![]() 分为面积比为1:3的两部分时,直接写出
分为面积比为1:3的两部分时,直接写出![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题提出:
如图所示,有三根针和套在一根针上的若干金属片,按下列规则,把金属片从一根针上全部移到另一根针上.

a.每次只能移动1个金属片;
b.较大的金属片不能放在较小的金属片上面.
把![]() 个金属片从1号针移到3号针,最少移动多少次?
个金属片从1号针移到3号针,最少移动多少次?
问题探究:为了探究规律,我们采用一般问题特殊化的方法,先从简单的情形入手,再逐次递进,最后得出一般性结论.
探究一:当![]() 时,只需把金属片从1号针移到3号针,用符号
时,只需把金属片从1号针移到3号针,用符号![]() 表示,共移动了1次.
表示,共移动了1次.
探究二:当![]() 时,为了避免将较大的金属片放在较小的金属片上面,我们利用2号针作为“中间针”,移动的顺序是:
时,为了避免将较大的金属片放在较小的金属片上面,我们利用2号针作为“中间针”,移动的顺序是:
a.把第1个金属片从1号针移到2号针;
b.把第2个金属片从1号针移到3号针;
c.把第1个金属片从2号针移到3号针.
用符号表示为:![]() ,
,![]() ,
,![]() .共移动了3次.
.共移动了3次.
探究三:当![]() 时,把上面两个金属片作为一个整体,则归结为
时,把上面两个金属片作为一个整体,则归结为![]() 的情形,移动的顺序是:
的情形,移动的顺序是:
a.把上面两个金属片从1号针移到2号针;
b.把第3个金属片从1号针移到3号针;
c.把上面两个金属片从2号针移到3号针.
其中(1)和(3)都需要借助中间针,用符号表示为:
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .共移动了7次.
.共移动了7次.
(1)探究四:请仿照前面步骤进行解答:当![]() 时,把上面3个金属片作为一个整体,移动的顺序是:___________________________________________________.
时,把上面3个金属片作为一个整体,移动的顺序是:___________________________________________________.
(2)探究五:根据上面的规律你可以发现当![]() 时,需要移动________次.
时,需要移动________次.
(3)探究六:把![]() 个金属片从1号针移到3号针,最少移动________次.
个金属片从1号针移到3号针,最少移动________次.
(4)探究七:如果我们把![]() 个金属片从1号针移到3号针,最少移动的次数记为
个金属片从1号针移到3号针,最少移动的次数记为![]() ,当
,当![]() 时如果我们把
时如果我们把![]() 个金属片从1号针移到3号针,最少移动的次数记为
个金属片从1号针移到3号针,最少移动的次数记为![]() ,那么
,那么![]() 与
与![]() 的关系是
的关系是![]() __________.
__________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com