
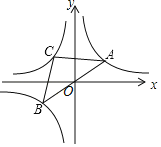
【题目】如图,已知A,B为反比例函数y1=![]() 图象上两点,连接AB,线段AB经过点O,C是反比例函数y2=
图象上两点,连接AB,线段AB经过点O,C是反比例函数y2=![]() (k<0)在第二象限内的图象上一点,当△CAB是以AB为底的等腰三角形,且
(k<0)在第二象限内的图象上一点,当△CAB是以AB为底的等腰三角形,且![]() 时,k的值为( )
时,k的值为( )
A.﹣![]() B.﹣3C.﹣4D.﹣
B.﹣3C.﹣4D.﹣![]()
【答案】A
【解析】
作AE⊥x轴于E,CF⊥x轴于F,通过证明△CFO∽△OEA,利用相似三角形面积比等于相似比的平方,求得△COF面积,再利用反比例函数系数k的几何意义,即k与面积之间的关系确定k值.
解:如图作AE⊥x轴于E,CF⊥x轴于F.连接OC.
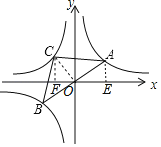
∵A、B关于原点对称,
∴OA=OB,
∵AC=BC,OA=OB,
∴OC⊥AB,
∴∠CFO=∠COA=∠AEO=90°,
∵∠COF+∠AOE=90°,∠AOE+∠EAO=90°,
∴∠COF=∠OAE,
∴△CFO∽△OEA,
∴![]() =(
=(![]() )2,
)2,
∵CA:AB=5:8,AO=OB,
∴CA:OA=5:4,
∴CO:OA=3:4,
∴![]() =(
=(![]() )2=
)2=![]() ,∵S△AOE=2,
,∵S△AOE=2,
∴S△COF=![]() ,
,
∴![]() =
=![]() ,
,
∵k<0,
∴k=-![]() ,
,
故选:A.


科目:初中数学 来源: 题型:
【题目】阅读材料,我们给出如下定义:若一个四边形中存在一组对边的平方和等于另一组对边的平方和,则称这个四边形为等平方和四边形.
(1)写出一个你所学过的特殊四边形中是等平方和四边形的图形的名称: .
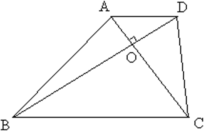
(2)如图,在梯形ABCD中,AD∥BC,AC⊥BD,垂足为O.
求证:![]() ,即四边形ABCD是等平方和四边形.
,即四边形ABCD是等平方和四边形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司计划6月底组织员工到某地旅游,参加旅游的人数估计为5-20人,甲、乙两家旅行社的服务质量相同,且报价都是每人200元.经过协商,甲旅行社表示可给予每位游客七折优惠;乙旅行社表示可先免去一位游客的旅游费用,其余游客八折优惠.请你帮他们算一算该公司应选择哪一家旅行社支付的旅游费用较少?
查看答案和解析>>
科目:初中数学 来源: 题型:
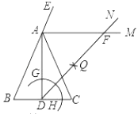
【题目】如图,在△ABC中,AB=AC=6,BC=4,AD是BC边上的高,AM是△ABC外角∠CAE的平分线.以点D为圆心,适当长为半径画弧,交DA于点G,交DC于点H.再分别以点G、H为圆心,大于![]() GH的长为半径画弧,两弧在∠ADC内部交于点Q,连接DQ并延长与AM交于点F,则DF的长度为( ).
GH的长为半径画弧,两弧在∠ADC内部交于点Q,连接DQ并延长与AM交于点F,则DF的长度为( ).
A.6B.![]() C.
C.![]() D.8
D.8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一方有难,八方支援.“新冠肺炎”疫情来袭,除了医务人员主动请缨逆行走向战场外,众多企业也伸出援助之手.某公司用甲,乙两种货车向武汉运送爱心物资,两次满载的运输情况如下表:
甲种货车辆数 | 乙种货车辆数 | 合计运物资吨数 | |
第一次 | 3 | 4 | 29 |
第二次 | 2 | 6 | 31 |
(1)求甲、乙两种货车每次满载分别能运输多少吨物资;
(2)目前有46.4吨物资要运输到武汉,该公司拟安排甲乙货车共10辆,全部物资一次运完,其中每辆甲车一次运送花费500元,每辆乙车一次运送花费300元,请问该公司应如何安排车辆最节省费用?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点A在x轴负半轴上,点B在y轴正半轴上,线段OB的长是方程x2﹣2x﹣8=0的解,tan∠BAO=![]() .
.
(1)求点A的坐标;
(2)点E在y轴负半轴上,直线EC⊥AB,交线段AB于点C,交x轴于点D,S△DOE=16.若反比例函数y=![]() 的图象经过点C,求k的值;
的图象经过点C,求k的值;
(3)在(2)条件下,点M是DO中点,点N,P,Q在直线BD或y轴上,是否存在点P,使四边形MNPQ是矩形?若存在,请直接写出点P的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
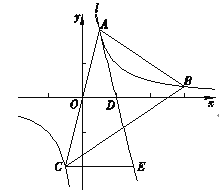
【题目】如图,在平面直角坐标系xOy中,点![]() ,
, ![]() 在反比例函数
在反比例函数![]() (m为常数)的图象上,连接AO并延长与图象的另一支有另一个交点为点C,过点A的直线l与x轴的交点为点
(m为常数)的图象上,连接AO并延长与图象的另一支有另一个交点为点C,过点A的直线l与x轴的交点为点![]() ,过点C作CE∥x轴交直线l于点E.
,过点C作CE∥x轴交直线l于点E.
(1)求m的值,并求直线l对应的函数解析式;
(2)求点E的坐标;
(3)过点B作射线BN∥x轴,与AE交于点M (补全图形),求证: ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=x2+bx+c与x轴交于点A(4,﹣5).
(1)如图,过点A分别向x轴、y轴作垂线,垂足分别为B、C,得到矩形ABOC,且抛物线经过点C.
①求抛物线的解析式.
②将抛物线沿直线x=m(2>m>0)翻折,分别交线段OB、AC于D,E两点.若直线DE刚好平分矩形ABOC的面积,求m的值.
(2)将抛物线旋转180°,使点A的对应点为A1(m﹣2,n﹣4),其中m≤2.若旋转后的抛物线仍然经过点A,求旋转后的抛物线顶点所能达到最低点时的坐标.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com