
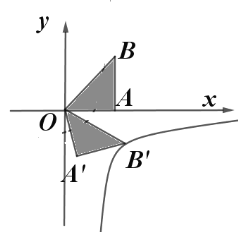
【题目】如图,等腰直角三角形![]() 的直角顶点
的直角顶点![]() 在
在![]() 轴的正半轴上,
轴的正半轴上,![]() ,将
,将![]() 绕顶点
绕顶点![]() 顺时针旋转
顺时针旋转![]() 至
至![]() ,使点
,使点![]() 落在双曲线
落在双曲线![]() 的图象上,则
的图象上,则![]() ________,该双曲线的函数解析式为________.
________,该双曲线的函数解析式为________.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】以下说法正确的有( )
①正八边形的每个内角都是135°
②![]() 与
与![]() 是同类二次根式
是同类二次根式
③长度等于半径的弦所对的圆周角为30°
④反比例函数y=﹣![]() ,当x<0时,y随x的增大而增大.
,当x<0时,y随x的增大而增大.
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中华文明,源远流长,中华汉字,寓意深广.为传承中华优秀传统文化,某中学德育处组织了一次全校2000名学生参加的“汉字听写”大赛.为了解本次大赛的成绩,学校德育处随机抽取了其中200名学生的成绩作为样本进行统计,制成如下不完整的统计图表:
成绩x(分)分数段 | 频数(人) | 频率 |
50≤x<60 | 10 | 0.05 |
60≤x<70 | 30 | 0.15 |
70≤x<80 | 40 | 0.2 |
80≤x<90 | m | 0.35 |
90≤x<100 | 50 | n |
频数分布直方图
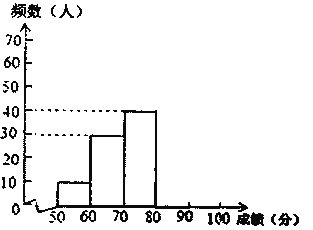
根据所给的信息,回答下列问题:
(1)m=________;n=________;
(2)补全频数分布直方图;
(3)这200名学生成绩的中位数会落在________分数段;
(4)若成绩在90分以上(包括90分)为“优”等,请你估计该校参加本次比赛的2000名学生中成绩是“优”等的约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】两人要去某风景区游玩,每天某一时段开往该风景区有三辆汽车(票价相同),但是他们不知道这些车的舒适程度,也不知道汽车开过来的顺序.两人采用了不同的乘车方案:甲无论如何总是上开来的第一辆车.而乙则是先观察后上车,当第一辆车开来时,他不上车,而是仔细观察车的舒适状况.如果第二辆车的状况比第一辆好,他就上第二辆车;如果第二辆不比第一辆好,他就上第三辆车.如果把这三辆车的舒适程度分为上、中、下三等,请尝试解决下面的问题:请用树状图或列表法分析,甲、乙两人采用的方案,哪一种方案使自己乘坐上等车的可能性大.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两车从![]() 地出发,沿同一路线驶向
地出发,沿同一路线驶向![]() 地.甲车先出发匀速驶向
地.甲车先出发匀速驶向![]() 地,
地,![]() 后乙出发,匀速行驶一段时间后,在途中的货站装货耗时半小时.由于满载货物,为了行驶安全,速度减少了
后乙出发,匀速行驶一段时间后,在途中的货站装货耗时半小时.由于满载货物,为了行驶安全,速度减少了![]() ,结果与甲车同时到达
,结果与甲车同时到达![]() 地,甲乙两车距
地,甲乙两车距![]() 地的路程
地的路程![]() 与乙车行驶时间
与乙车行驶时间![]() 之间的函数图象如图所示
之间的函数图象如图所示
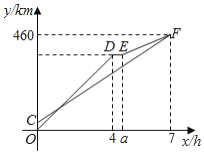
(1)![]() 的值是________,甲的速度是________
的值是________,甲的速度是________![]() .
.
(2)求乙车距![]() 地的路程
地的路程![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(3)若甲乙两车距离不超过![]() 时,车载通话机可以进行通话,则两车在行驶过程中可以通话的总时长为多少小时?
时,车载通话机可以进行通话,则两车在行驶过程中可以通话的总时长为多少小时?
查看答案和解析>>
科目:初中数学 来源: 题型:
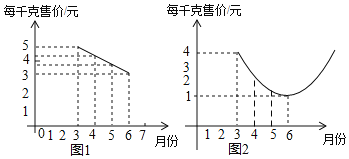
【题目】某种蔬菜的销售单价y1与销售月份x之间的关系如图1所示,成本y2与销售月份x之间的关系如图2所示(图1的图象是线段,图2的图象是抛物线)
(1)已知6月份这种蔬菜的成本最低,此时出售每千克的收益是多少元?(收益=售价﹣成本)
(2)哪个月出售这种蔬菜,每千克的收益最大?简单说明理由.
(3)已知市场部销售该种蔬菜4、5两个月的总收益为22万元,且5月份的销售量比4月份的销售量多2万千克,求4、5两个月的销售量分别是多少万千克?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() .点
.点![]() 从点
从点![]() 出发,以每秒3个单位长度的速度向终点
出发,以每秒3个单位长度的速度向终点![]() 运动,过点
运动,过点![]() 作
作![]() 交
交![]() 边或
边或![]() 边于点
边于点![]() ,点
,点![]() 是射线
是射线![]() 边上一点,总保持
边上一点,总保持![]() ,以
,以![]() 、
、![]() 为邻边构造矩形
为邻边构造矩形![]() ,设矩形
,设矩形![]() 与
与![]() 重叠部分图形的面积为
重叠部分图形的面积为![]() ,点
,点![]() 的运动时间为
的运动时间为![]() .
.
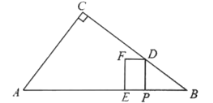
(1)用含![]() 的式子表示线段
的式子表示线段![]() 的长;
的长;
(2)当点![]() 落在
落在![]() 上时,求
上时,求![]() 的值;
的值;
(3)当矩形![]() 与
与![]() 重叠部分图形为四边形时,求
重叠部分图形为四边形时,求![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(4)点![]() 与点
与点![]() 同时出发,在线段
同时出发,在线段![]() 上以每秒5个单位长度的速度沿
上以每秒5个单位长度的速度沿![]() 往返一次,连结
往返一次,连结![]() 、
、![]() ,直接写出矩形
,直接写出矩形![]() 的面积是
的面积是![]() 的面积的2倍时
的面积的2倍时![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
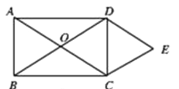
【题目】矩形ABCD的对角线相交于点O.DE∥AC,CE∥BD.
(1)求证:四边形OCED是菱形;
(2)若∠ACB=30°,菱形OCED的而积为![]() ,求AC的长.
,求AC的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com