
【题目】甲、乙两车从![]() 地出发,沿同一路线驶向
地出发,沿同一路线驶向![]() 地.甲车先出发匀速驶向
地.甲车先出发匀速驶向![]() 地,
地,![]() 后乙出发,匀速行驶一段时间后,在途中的货站装货耗时半小时.由于满载货物,为了行驶安全,速度减少了
后乙出发,匀速行驶一段时间后,在途中的货站装货耗时半小时.由于满载货物,为了行驶安全,速度减少了![]() ,结果与甲车同时到达
,结果与甲车同时到达![]() 地,甲乙两车距
地,甲乙两车距![]() 地的路程
地的路程![]() 与乙车行驶时间
与乙车行驶时间![]() 之间的函数图象如图所示
之间的函数图象如图所示
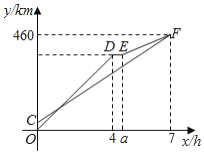
(1)![]() 的值是________,甲的速度是________
的值是________,甲的速度是________![]() .
.
(2)求乙车距![]() 地的路程
地的路程![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(3)若甲乙两车距离不超过![]() 时,车载通话机可以进行通话,则两车在行驶过程中可以通话的总时长为多少小时?
时,车载通话机可以进行通话,则两车在行驶过程中可以通话的总时长为多少小时?
【答案】(1)4.5;60;(2)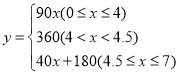 ;(3)
;(3)![]() 小时
小时
【解析】
(1)由乙在途中的货站装货耗时半小时易得a=4.5,甲从A到B共用了(![]() +7)小时,然后利用速度公式计算甲的速度;
+7)小时,然后利用速度公式计算甲的速度;
(2)分段函数;设乙开始的速度为v千米/小时,利用乙两段时间内的路程和为460列方程4v+(7-4.5)(v-50)=460,解得v=90(千米/小时),计算出4v=360,则可得到D(4,360),E(4.5,360),然后利用待定系数法求出线段EF所表示的y与x的函数关系式为y=40x+180(4.5≤x≤7);
(3)求出线段CF的解析式,再根据题意列不等式组解答即可.
解:(1)∵线段![]() 代表乙车在途中的货站装货耗时半小时,
代表乙车在途中的货站装货耗时半小时,
∴![]() (小时),
(小时),
甲车的速度=![]() =60(千米/小时);
=60(千米/小时);
故答案为:4.5;60;
(2)设乙开始的速度为![]() 千米/小时,
千米/小时,
则![]() ,解得
,解得![]() (千米/小时),
(千米/小时),
![]() ,
,
则![]() ,
,![]() ,
,
∴线段![]() 的函数关系式为
的函数关系式为![]() (
(![]() ),
),
设直线![]() 的解析式为
的解析式为![]() ,
,
![]() ,解得
,解得![]() ,
,
所以线段![]() 所表示的
所表示的![]() 与
与![]() 的函数关系式为
的函数关系式为![]() (
(![]() );
);
综上所述,乙车距![]() 地的路程
地的路程![]() 与
与![]() 之间的函数关系式为:
之间的函数关系式为:
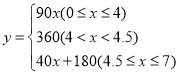 ;
;
(3)易知![]() ,
,
设线段![]() 的解析式为
的解析式为![]() ,根据题意得,
,根据题意得,
![]() ,解得
,解得![]() ,
,
∴线段![]() 的解析式为
的解析式为![]() ,
,
∵甲乙两车距离不超过![]() 时,车载通话机可以进行通话,
时,车载通话机可以进行通话,
∴![]() ,解得
,解得![]() ,
,
![]() ,解得
,解得![]() ,
,
则两车在行驶过程中可以通话的总时长为:![]() (小时).
(小时).


 小夫子全能检测系列答案
小夫子全能检测系列答案科目:初中数学 来源: 题型:
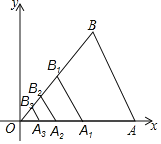
【题目】如图,在平面直角标系xOy中,以O为位似中心,将边长为8的等边三角形OAB作n次位似变换,经第一次变换后得到等边三角形OA1B1,其边长OA1缩小为OA的![]() ,经第二次变换后得到等边三角形OA2B2,其边长OA2缩小为OA1的
,经第二次变换后得到等边三角形OA2B2,其边长OA2缩小为OA1的![]() ,经第三次变换后得到等边三角形OA3B3,其边长OA3缩小为OA2的
,经第三次变换后得到等边三角形OA3B3,其边长OA3缩小为OA2的![]() ,…按此规律,经第n次变换后,所得等边出角形OAnBn.的顶点An的坐标为(
,…按此规律,经第n次变换后,所得等边出角形OAnBn.的顶点An的坐标为(![]() ,0),则n的值是( )
,0),则n的值是( )
A. 8 B. 9 C. 10 D. 11
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,是甲、乙两种机器人根据电脑程序工作时各自工作量y关于工作时间x的函数图像,线段OA表示甲机器人的工作量![]() (吨)关于时间x(时)的函数图像,线段BC表示乙机器人的工作量
(吨)关于时间x(时)的函数图像,线段BC表示乙机器人的工作量![]() (吨)关于时间x(时)的函数图像.根据图像信息回答下列填空题.
(吨)关于时间x(时)的函数图像.根据图像信息回答下列填空题.
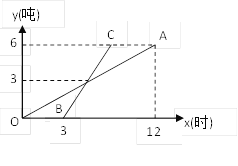
(1)甲种机器人比乙种机器人早开始工作 小时;甲种机器人每小时的工作量是 吨;
(2)直线BC的表达式为 ;当乙种机器人工作5小时后,它完成的工作量是 吨.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,![]() 是
是![]() 外一点,过点
外一点,过点![]() 做
做![]() 的两条切线,切点分别为
的两条切线,切点分别为![]() .若
.若![]() ,则点
,则点![]() 叫做
叫做![]() 的切角点.
的切角点.
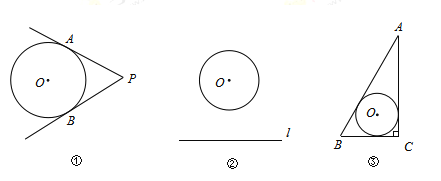
(1)如图②,![]() 的半径是1,点O到直线
的半径是1,点O到直线![]() 的距离为2.若点
的距离为2.若点![]() 是
是![]() 的切角点,且点
的切角点,且点![]() 在直线
在直线![]() 上,请用尺规作出点
上,请用尺规作出点![]() ;(保留作图痕迹,不写作法)
;(保留作图痕迹,不写作法)
(2)如图③,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 是
是![]() 的内切圆.若点
的内切圆.若点![]() 是
是![]() 的切角点,且点
的切角点,且点![]() 在
在![]() 的边上,求
的边上,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了让同学们了解自己的体育水平,初二1班的体育刘老师对全班45名学生进行了一次体育模拟测试(得分均为整数),成绩满分为10分,1班的体育委员根据这次测试成绩,制作了统计图和分析表如下:
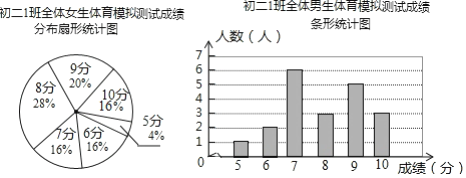
初二1班体育模拟测试成绩分析表
平均分 | 方差 | 中位数 | 众数 | |
男生 | ________ | 2 | 8 | 7 |
女生 | 7.92 | 1.99 | 8 | ________ |
根据以上信息,解答下列问题:
(1)这个班共有男生________人,共有女生________人;
(2)补全初二1班体育模拟测试成绩分析表;
(3)你认为在这次体育测试中,1班的男生队、女生队哪个表现更突出一些?并写出一条支持你的看法的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在一个可以自由转动的转盘中,指针位置固定,三个扇形的面积都相等,且分别标有数字1,2,3.

(1)小明转动转盘一次,当转盘停止转动时,指针所指扇形中的数字是奇数的概率为________;
(2)小明先转动转盘一次,当转盘停止转动时,记录下指针所指扇形中的数字;接着再转动转盘一次,当转盘停止转动时,再次记录下指针所指扇形中的数字,求这两个数字之和是3的倍数的概率(用画树状图或列表等方法求解)
查看答案和解析>>
科目:初中数学 来源: 题型:
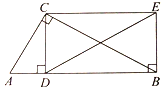
【题目】如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D ,BE⊥AB,垂足为B,BE=CD连接CE,DE.
(1)求证:四边形CDBE是矩形
(2)若AC=2 ,∠ABC=30°,求DE的长
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商品的进价为每件50元.当售价为每件70元时,每星期可卖出300件,现需降价处理,且经市场调查:每降价1元,每星期可多卖出20件.在确保盈利的前提下,解答下列问题:
(1)若设每件降价x元、每星期售出商品的利润为y元,请写出y与x的函数关系式,并求出自变量x的取值范围;
(2)当降价多少元时,每星期的利润最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学问题:如何计算平面直角坐标系中任意两点之间的距离?
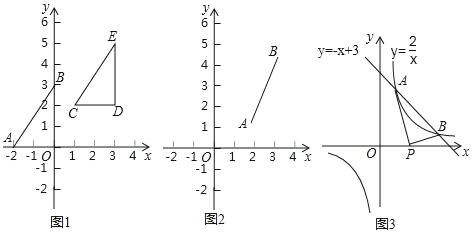
探究问题:
为解决上面的问题,我们从最简单的问题进行研究.
探究一:在图1中,已知线段AB,A(﹣2,0),B(0,3),写出线段AO的长,BO的长,所以线段AB的长为多少;把Rt△AOB向右平移3个单位,再向上平移2个单位,得到Rt△CDE,写出Rt△CDE的顶点坐标C,D,E,此时线段CD的长为多少,DE的长为多少,所以线段CE的长为多少.
探究二:在图2中,已知线段AB的端点坐标为A(a,b),B(c,d),求出图中AB的长(用含a,b,c,d的代数式表示,不必证明).
归纳总结:无论线段AB处于直角坐标系中的哪个位置,当其端点坐标为A(x1,y1),B(x2,y2)时线段AB的长为多少(用含x1,y1,x2,y2的代数式表示,不必证明).
拓展与应用:
运用在图3中,一次函数y=﹣x+3与反比例函数y=![]() 的图象交点为A、B,交点的坐标分别是A(1,2),B(2,1).
的图象交点为A、B,交点的坐标分别是A(1,2),B(2,1).
①求线段AB的长;
②若点P是x轴上动点,求PA+PB的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com