
【题目】在平面直角坐标系中,矩形![]() 的顶点
的顶点![]() (1,0),
(1,0),![]() (0,2),点
(0,2),点![]() 在第一象限,
在第一象限,![]() ∥
∥![]() 轴,若函数
轴,若函数![]() =
=![]() 的图象经过矩形
的图象经过矩形![]() 的对角线的交点,则
的对角线的交点,则![]() 的值为( )
的值为( )
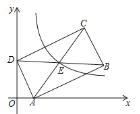
A.4B.5C.8D.10
【答案】B
【解析】
根据平行于x轴的直线上任意两点纵坐标相同,可设B(x,2).利用矩形的性质得出E为BD中点,∠DAB=90°.根据线段中点坐标公式得出E(![]() x,2).由勾股定理得出AD2+AB2=BD2,列出方程12+22+(x-1)2+22=x2,求出x,得到E点坐标,代入y=
x,2).由勾股定理得出AD2+AB2=BD2,列出方程12+22+(x-1)2+22=x2,求出x,得到E点坐标,代入y=![]() ,利用待定系数法求出k.
,利用待定系数法求出k.
∵BD∥x轴,D(0,2),
∴B、D两点纵坐标相同,都为2,
∴可设B(x,2).
∵矩形ABCD的对角线的交点为E,
∴E为BD中点,∠DAB=90°.
∴E(![]() x,2).
x,2).
∵∠DAB=90°,
∴AD2+AB2=BD2,
∵A(1,0),D(0,2),B(x,2),
∴12+22+(x-1)2+22=x2,
解得x=5,
∴E(![]() ,2).
,2).
∵反比例函数y=![]() (k>0,x>0)的图象经过点E,
(k>0,x>0)的图象经过点E,
∴k=![]() ×2=5.
×2=5.
故选:B.


科目:初中数学 来源: 题型:
【题目】两人要去某风景区游玩,每天某一时段开往该风景区有三辆汽车(票价相同),但是他们不知道这些车的舒适程度,也不知道汽车开过来的顺序.两人采用了不同的乘车方案:甲无论如何总是上开来的第一辆车.而乙则是先观察后上车,当第一辆车开来时,他不上车,而是仔细观察车的舒适状况.如果第二辆车的状况比第一辆好,他就上第二辆车;如果第二辆不比第一辆好,他就上第三辆车.如果把这三辆车的舒适程度分为上、中、下三等,请尝试解决下面的问题:请用树状图或列表法分析,甲、乙两人采用的方案,哪一种方案使自己乘坐上等车的可能性大.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】教材呈现:下图是华师版八年级下册数学教材第11页的部分内容.
例1,如图,在菱形![]() 中,
中,![]() ,试求
,试求![]() 的大小,并说明
的大小,并说明![]() 是等边三角形
是等边三角形
问题解决:请结合图(1),写出例1的完整解答过程;

问题探究:在菱形![]() 中,对角线
中,对角线![]() 相交于点
相交于点![]() ,过点D作
,过点D作![]() 交BC的延长线于点E.
交BC的延长线于点E.
(1)如图2,连接OE,则OE的长为____________;
(2)如图3,若点P是对角线BD上一动点,连结![]() ,则
,则![]() 的最小值为____________.
的最小值为____________.
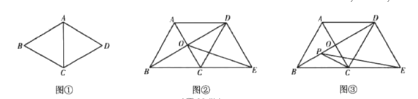
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】儿童用药的剂量常常按他们的体重来计算,某种药品,体重![]() 的儿童,每次正常服用量为
的儿童,每次正常服用量为![]() ;体重
;体重![]() 的儿童每次正常服用量为
的儿童每次正常服用量为![]() ;体重在
;体重在![]() 范围内时,每次正常服用量
范围内时,每次正常服用量![]() 是儿童体重
是儿童体重![]() 的一次函数中,现实中,该药品每次实际服用量可以比每次正常服用略高一些,但不能超过正常服用量的1.2倍,否则会对儿童的身体造成较大损害.
的一次函数中,现实中,该药品每次实际服用量可以比每次正常服用略高一些,但不能超过正常服用量的1.2倍,否则会对儿童的身体造成较大损害.
(1)求![]() 与
与![]() 之间的函数关系式,并写出自变量
之间的函数关系式,并写出自变量![]() 的取值范围;
的取值范围;
(2)若该药品的一种包装规格为![]() /袋,求体重在什么范围的儿童生病时可以一次服下一袋药?
/袋,求体重在什么范围的儿童生病时可以一次服下一袋药?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△![]() 中,高
中,高![]() =3,∠
=3,∠![]() =45°,
=45°,![]() =
=![]() ,动点
,动点![]() 从点
从点![]() 出发,沿
出发,沿![]() 方向以每秒1个单位长度的速速向终点
方向以每秒1个单位长度的速速向终点![]() 运动,当点
运动,当点![]() 与点
与点![]() 、
、![]() 不重合时,过点
不重合时,过点![]() 作
作![]() 、
、![]() 的平行线,与
的平行线,与![]() 分别交于点
分别交于点![]() 、
、![]() ,将△
,将△![]() 绕
绕![]() 的中点旋转180°得△
的中点旋转180°得△![]() ,设点
,设点![]() 的运动时间为
的运动时间为![]() 秒,△
秒,△![]() 与△
与△![]() 重叠部分面积为
重叠部分面积为![]() .
.
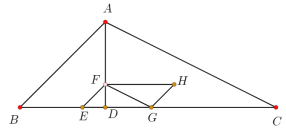
(1)当![]() = 秒时,点
= 秒时,点![]() 落在
落在![]() 边上.
边上.
(2)求![]() 与
与![]() 的函数关系式.
的函数关系式.
(3)当直线![]() 将△
将△![]() 分为面积比为1:3的两部分时,直接写出
分为面积比为1:3的两部分时,直接写出![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
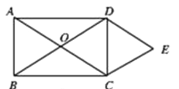
【题目】矩形ABCD的对角线相交于点O.DE∥AC,CE∥BD.
(1)求证:四边形OCED是菱形;
(2)若∠ACB=30°,菱形OCED的而积为![]() ,求AC的长.
,求AC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某小微企业为加快产业转型升级步伐,引进一批A,B两种型号的机器.已知一台A型机器比一台B型机器每小时多加工2个零件,且一台A型机器加工80个零件与一台B型机器加工60个零件所用时间相等.
(1)每台A,B两种型号的机器每小时分别加工多少个零件?
(2)如果该企业计划安排A,B两种型号的机器共10台一起加工一批该零件,为了如期完成任务,要求两种机器每小时加工的零件不少于72件,同时为了保障机器的正常运转,两种机器每小时加工的零件不能超过76件,那么A,B两种型号的机器可以各安排多少台?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c经过点B(4,0),C(0,﹣2),对称轴为直线x=1,与x轴的另一个交点为点A.
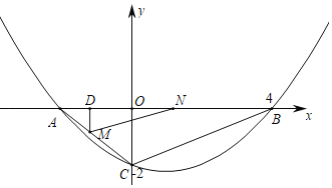
(1)求抛物线的解析式;
(2)点M从点A出发,沿AC向点C运动,速度为1个单位长度/秒,同时点N从点B出发,沿BA向点A运动,速度为2个单位长度/秒,当点M、N有一点到达终点时,运动停止,连接MN,设运动时间为t秒,当t为何值时,AMN的面积S最大,并求出S的最大值;
(3)点P在x轴上,点Q在抛物线上,是否存在点P、Q,使得以点P、Q、B、C为顶点的四边形是平行四边形,若存在,直接写出所有符合条件的点P坐标,若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com