
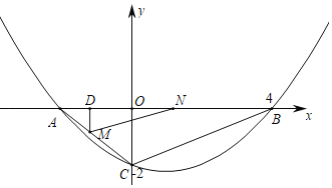
°æƒø°ø»ÁÕº£¨≈◊ŒÔœþy£Ωax2+bx+cæ≠π˝µ„B(4£¨0)£¨C(0£¨©Å2)£¨∂‘≥∆÷·Œ™÷±œþx£Ω1£¨”Îx÷·µƒ¡Ì“ª∏ˆΩªµ„Œ™µ„A£Æ
£®1£©«Û≈◊ŒÔœþµƒΩ‚Œˆ Ω£ª
£®2£©µ„M¥”µ„A≥ˆ∑¢£¨—ÿACœÚµ„C‘À∂Ø£¨ÀŸ∂»Œ™1∏ˆµ•Œª≥§∂»/√Σ¨Õ¨ ±µ„N¥”µ„B≥ˆ∑¢£¨—ÿBAœÚµ„A‘À∂Ø£¨ÀŸ∂»Œ™2∏ˆµ•Œª≥§∂»/√Σ¨µ±µ„M°¢N”–“ªµ„µΩ¥Ô÷’µ„ ±£¨‘À∂ØÕ£÷π£¨¡¨Ω”MN£¨…Ë‘À∂Ø ±º‰Œ™t√Σ¨µ±tŒ™∫Œ÷µ ±£¨AMNµƒ√ʪ˝S◊Ó¥Û£¨≤¢«Û≥ˆSµƒ◊Ó¥Û÷µ£ª
£®3£©µ„P‘⁄x÷·…œ£¨µ„Q‘⁄≈◊ŒÔœþ…œ£¨ «∑ҥʑ⁄µ„P°¢Q£¨ πµ√“‘µ„P°¢Q°¢B°¢CŒ™∂•µ„µƒÀƒ±þ–Œ «∆Ω––Àƒ±þ–Œ£¨»Ù¥Ê‘⁄£¨÷±Ω”–¥≥ˆÀ˘”–∑˚∫œÃıº˛µƒµ„P◊¯±Í£¨»Ù≤ª¥Ê‘⁄£¨«ÎÀµ√˜¿Ì”…£Æ
°æ¥∞∏°ø£®1£©![]() £ª£®2£©µ±
£ª£®2£©µ±![]() ±£¨S◊Ó¥Û÷µŒ™
±£¨S◊Ó¥Û÷µŒ™![]() £ª£®3£©¥Ê‘⁄£¨P1(©Å3+
£ª£®3£©¥Ê‘⁄£¨P1(©Å3+![]() £¨0)£¨P2(©Å3©Å
£¨0)£¨P2(©Å3©Å![]() £¨0)£¨P3(6£¨0)£¨P4(2£¨0)
£¨0)£¨P3(6£¨0)£¨P4(2£¨0)
°æΩ‚Œˆ°ø
£®1£©¿˚”√¥˝∂®œµ ˝∑®»∑∂®∫Ø ˝Ω‚Œˆ Ω£ª
£®2£©”…≈◊ŒÔœþµƒ∂‘≥∆–‘÷ «Ûµ√A£®-2£¨0£©£¨‘ÚAB=6£ªµ±µ„N‘À∂Øt√Î ±£¨BN=2t£¨‘ÚAN=6-2t£¨π˝µ„M◊˜MD°Õx÷·”⁄µ„D£¨ππ‘Ï÷±Ω«»˝Ω«–Œ£¨”…»˝Ω«–Œµƒ√ʪ˝π´ Ω¡–≥ˆ∫Ø ˝πÿœµ Ω£¨¿˚”√≈‰∑Ω∑®«Ûµ√◊Ó¥Û÷µ£ª
£®3£©–Ë“™∑÷»˝÷÷«ÈøˆÃ÷¬€£¨”√∆Ω“∆µƒ÷™ ∂œ»«Û≥ˆµ„Qµƒ∫·◊¯±Í£¨»ª∫ÛÕ∆≥ˆµ„Pµƒ◊¯±Í£Æ
£®1£©“¿Ã‚“‚£¨Ω´B£®4£¨0£©£¨C£®0£¨©Å2£©£¨∂‘≥∆÷·Œ™÷±œþx£Ω1£¨¥˙»Î≈◊ŒÔœþΩ‚Œˆ Ω£¨
µ√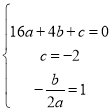 £¨
£¨
Ω‚µ√£∫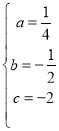 £¨
£¨
°ý≈◊ŒÔœþµƒΩ‚Œˆ ΩŒ™£∫![]() £ª
£ª
£®2£©°þ∂‘≥∆÷·Œ™÷±œþx£Ω1£¨B£®4£¨0£©£Æ
°ýA£®©Å2£¨0£©£¨‘ÚAB£Ω6£¨
µ±µ„N‘À∂Øt√Î ±£¨BN£Ω2t£¨‘ÚAN£Ω6©Å2t£¨
»ÁÕº1£¨π˝µ„M◊˜MD°Õx÷·”⁄µ„D£Æ
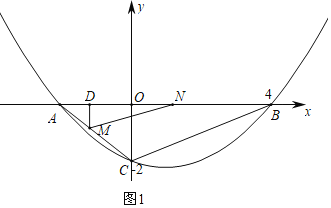
°þOA£ΩOC£Ω2£¨
°ý°˜OAC «µ»—¸÷±Ω«»˝Ω«–Œ£¨
°ý°œOAC£Ω45°„£Æ
”÷°þDM°ÕOA£¨
°ý°˜DAM «µ»—¸÷±Ω«»˝Ω«–Œ£¨AD£ΩDM£¨
µ±µ„M‘À∂Øt√Î ±£¨AM£Ωt£¨
°ýMD2+AD2£ΩAM2£Ωt2£¨
°ýDM£Ω![]() £¨
£¨
°ý![]() £¨
£¨
°þ![]() £¨
£¨
°ý”…∂˛¥Œ∫Ø ˝µƒÕºœÛº∞–‘÷ ø…÷™£¨µ±![]() ±£¨S◊Ó¥Û÷µŒ™
±£¨S◊Ó¥Û÷µŒ™![]() £ª
£ª
£®3£©¥Ê‘⁄£¨¿Ì”…»Áœ¬£∫
¢Ÿµ±Àƒ±þ–ŒCBQPŒ™∆Ω––Àƒ±þ–Œ ±£¨CB”ÎPQ∆Ω––«“œýµ»£¨
°þB£®4£¨0£©£¨C£®0£¨©Å2£©£¨
°ýyB©ÅyC£ΩyQ©ÅyP£Ω2£¨xB©ÅxC£ΩxQ©ÅxP£Ω4£¨
°þyP£Ω0£¨
°ýyQ£Ω2£¨
Ω´y£Ω2¥˙»Î![]() £¨
£¨
µ√ x1£Ω![]() £¨x2£Ω
£¨x2£Ω![]() £¨
£¨
°ýµ±xQ£Ω![]() ±£¨xP£Ω
±£¨xP£Ω![]() £ªµ±xQ£Ω
£ªµ±xQ£Ω![]() ±£¨xP£Ω
±£¨xP£Ω![]() £¨
£¨
°ýP1£®![]() £¨0£©£¨P2£®
£¨0£©£¨P2£®![]() £¨0£©£ª
£¨0£©£ª
¢⁄µ±Àƒ±þ–ŒCQPBŒ™∆Ω––Àƒ±þ–Œ ±£¨BP”ÎCQ∆Ω––«“œýµ»£¨
°þyP£ΩyB£Ω0£¨
°ýyQ£ΩyC£Ω©Å2£¨
Ω´y£Ω©Å2¥˙»Î![]() £¨
£¨
µ√ x1£Ω0£®…·»•£©£¨x2£Ω2£¨
°ýxQ£Ω2 ±£¨
°ýxP©ÅxB£ΩxQ©ÅxC£Ω2£¨
°ýxP£Ω6£¨
°ýP3£®6£¨0£©£ª
¢€µ±Àƒ±þ–ŒCQBPŒ™∆Ω––Àƒ±þ–Œ ±£¨BP”ÎCQ∆Ω––«“œýµ»£¨
”…¢⁄÷™£¨xQ£Ω2£¨
°ýxB©ÅxP£ΩxQ©ÅxC£Ω2£¨
°ýxP£Ω2£¨
°ýP4£®2£¨0£©£ª
◊€…œÀ˘ ˆ£¨¥Ê‘⁄¬˙◊„Ãıº˛µƒµ„P”–4∏ˆ£¨∑÷± «P1£®©Å3+![]() £¨0£©£¨P2£®©Å3©Å
£¨0£©£¨P2£®©Å3©Å![]() £¨0£©£¨P3£®6£¨0£©£¨P4£®2£¨0£©£Æ
£¨0£©£¨P3£®6£¨0£©£¨P4£®2£¨0£©£Æ


 ∫ƺŸÃϵÿ÷ÿ«Ï≥ˆ∞Ê…Áœµ¡–¥∞∏
∫ƺŸÃϵÿ÷ÿ«Ï≥ˆ∞Ê…Áœµ¡–¥∞∏
| ƒÍº∂ | ∏þ÷–øŒ≥à | ƒÍº∂ | ≥ı÷–øŒ≥à |
| ∏þ“ª | ∏þ“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı“ª | ≥ı“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ∂˛ | ∏þ∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı∂˛ | ≥ı∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ»˝ | ∏þ»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı»˝ | ≥ı»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° |
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
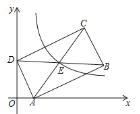
°æƒø°ø‘⁄∆Ω√Ê÷±Ω«◊¯±Íœµ÷–£¨æÿ–Œ![]() µƒ∂•µ„
µƒ∂•µ„![]() £®1,0£©£¨
£®1,0£©£¨![]() £®0,2£©£¨µ„
£®0,2£©£¨µ„![]() ‘⁄µ⁄“ªœÛœÞ£¨
‘⁄µ⁄“ªœÛœÞ£¨![]() °Œ
°Œ![]() ÷·£¨»Ù∫Ø ˝
÷·£¨»Ù∫Ø ˝![]() £Ω
£Ω![]() µƒÕºœÛæ≠π˝æÿ–Œ
µƒÕºœÛæ≠π˝æÿ–Œ![]() µƒ∂‘Ω«œþµƒΩªµ„£¨‘Ú
µƒ∂‘Ω«œþµƒΩªµ„£¨‘Ú![]() µƒ÷µŒ™£® £©
µƒ÷µŒ™£® £©
A.4B.5C.8D.10
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø‘⁄—ßœ∞°∞÷·∂‘≥∆œ÷œÛ°±ƒ⁄»ð ±£¨¿œ ¶»√Õ¨—ß√«—∞’“…̱þµƒ÷·∂‘≥∆Õº–Œ£¨–°√˜¿˚”√ ÷÷–µƒ“ª∏±»˝Ω«≥þ∫Õ“ª∏ˆ¡øΩ«∆˜£®»ÁÕºÀ˘ æ£©Ω¯––ÃΩæø£Æ
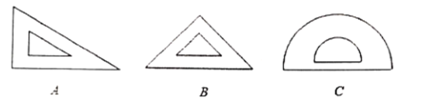
£®1£©–°√˜‘⁄’‚»˝º˛Œƒæþ÷–»Œ»°“ªº˛£¨Ω·π˚ «÷·∂‘≥∆Õº–Œµƒ∏≈¬ «_________£ª£®»°»˝º˛÷–»Œ“‚“ªº˛µƒø…ƒÐ–‘œýÕ¨£©
£®2£©–°√˜∑¢œ÷‘⁄![]() °¢
°¢![]() ¡Ω∞—»˝Ω«≥þ÷–∏˜—°“ª∏ˆΩ«∆¥‘⁄“ª∆£®ŒÞ÷ÿµ˛ŒÞ∑Ïœ∂£©ª·µ√µΩ“ª∏ˆ∏¸¥ÛµƒΩ«£¨»Ù√ø∏ˆΩ«—°»°µƒø…ƒÐ–‘œýÕ¨£¨«Î”√ª≠ ˜◊¥ÕºªÚ¡–±Ìµƒ∑Ω∑®Àµ√˜∆¥≥…µƒΩ« «∂€Ω«µƒ∏≈¬ «∂ý…Ÿ£Æ
¡Ω∞—»˝Ω«≥þ÷–∏˜—°“ª∏ˆΩ«∆¥‘⁄“ª∆£®ŒÞ÷ÿµ˛ŒÞ∑Ïœ∂£©ª·µ√µΩ“ª∏ˆ∏¸¥ÛµƒΩ«£¨»Ù√ø∏ˆΩ«—°»°µƒø…ƒÐ–‘œýÕ¨£¨«Î”√ª≠ ˜◊¥ÕºªÚ¡–±Ìµƒ∑Ω∑®Àµ√˜∆¥≥…µƒΩ« «∂€Ω«µƒ∏≈¬ «∂ý…Ÿ£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°øŒ™µ˜≤Èπ„Œ˜±±≤øÕÂÀƒ – –√Ò…œ∞ý ±◊Ó≥£”√µƒΩªÕ®π§æþµƒ«Èøˆ£¨Àʪ˙≥È»°¡ÀÀƒ –≤ø∑÷ –√ÒΩ¯––µ˜≤È£¨“™«Û±ªµ˜≤È’þ¥”°∞A£∫◊‘––≥µ£¨B£∫µÁ∂Ø≥µ£¨C£∫π´Ωª≥µ£¨D£∫º“Õ•∆˚≥µ£¨E£∫∆‰À˚°±ŒÂ∏ˆ—°œÓ÷–—°‘Ò◊Ó≥£”√µƒ“ªœÓ£¨Ω´À˘”–µ˜≤ÈΩ·π˚’˚¿Ì∫ÛªÊ÷∆≥…»Áœ¬≤ªÕÍ’˚µƒÃı–ŒÕ≥º∆Õº∫Õ…»–ŒÕ≥º∆Õº£¨«ÎΩ·∫œÕ≥º∆Õºªÿ¥œ¬¡–Œ £∫

£®1£©‘⁄’‚¥Œµ˜≤È÷–£¨“ªπ≤µ˜≤È¡À √˚ –√Ò£¨…»–ŒÕ≥º∆Õº÷–£¨C◊È∂‘”¶µƒ…»–Œ‘≤–ƒΩ« « °„£ª
£®2£©«Î≤π»´Ãı–ŒÕ≥º∆Õº£ª
£®3£©»Ùº◊°¢““¡Ω»À…œ∞ý ±¥”A°¢B°¢C°¢DÀƒ÷÷ΩªÕ®π§æþ÷–Àʪ˙—°‘Ò“ª÷÷£¨‘Úº◊°¢““¡Ω»À«°∫√—°‘ÒÕ¨“ª÷÷ΩªÕ®π§æþ…œ∞ýµƒ∏≈¬ «∂ý…Ÿ£ø«Î”√ª≠ ˜◊¥ÕºªÚ¡–±Ì∑®«ÛΩ‚£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
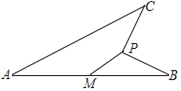
°æƒø°ø»ÁÕº£¨œþ∂ŒAB£Ω4£¨MŒ™ABµƒ÷–µ„£¨∂ص„PµΩµ„Mµƒæý¿Î «1£¨¡¨Ω”PB£¨œþ∂ŒPB»∆µ„PƒÊ ±’Ζ˝◊™90°„µ√µΩœþ∂ŒPC£¨¡¨Ω”AC£¨‘Úœþ∂ŒAC≥§∂»µƒ◊Ó¥Û÷µ «_____£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
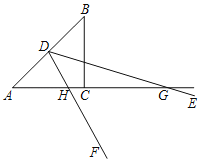
°æƒø°ø»ÁÕº£¨‘⁄µ»—¸Rt°˜ABC÷–£¨AC£ΩBC£Ω6![]() £¨°œEDFµƒ∂•µ„D «ABµƒ÷–µ„£¨«“°œEDF£Ω45°„£¨œ÷Ω´°œEDF»∆µ„D–˝◊™“ª÷У¨‘⁄–˝◊™π˝≥Ã÷–£¨µ±°œEDFµƒ¡Ω±þDE°¢DF∑÷±Ωª÷±œþAC”⁄µ„G°¢H£¨∞—°˜DGH—ÿDH’€µ˛£¨µ„G¬‰‘⁄µ„M¥¶£¨¡¨Ω”AM£¨»Ù
£¨°œEDFµƒ∂•µ„D «ABµƒ÷–µ„£¨«“°œEDF£Ω45°„£¨œ÷Ω´°œEDF»∆µ„D–˝◊™“ª÷У¨‘⁄–˝◊™π˝≥Ã÷–£¨µ±°œEDFµƒ¡Ω±þDE°¢DF∑÷±Ωª÷±œþAC”⁄µ„G°¢H£¨∞—°˜DGH—ÿDH’€µ˛£¨µ„G¬‰‘⁄µ„M¥¶£¨¡¨Ω”AM£¨»Ù![]() £Ω
£Ω![]() £¨‘ÚAHµƒ≥§Œ™_______£Æ
£¨‘ÚAHµƒ≥§Œ™_______£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
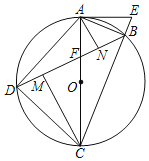
°æƒø°ø»ÁÕº£¨Àƒ±þ–ŒABCDƒ⁄Ω””⁄°—O£¨∂‘Ω«œþAC°¢BDœýΩª”⁄µ„F£¨AC «°—Oµƒ÷±æ∂£¨—”≥§CBµΩµ„E£¨¡¨Ω”AE£¨°œBAE£Ω°œADB£¨AN°ÕBD£¨CM°ÕBD£¨¥π◊„∑÷±Œ™µ„N°¢M£Æ
£®1£©÷§√˜£∫AE «°—Oµƒ«–œþ£ª
£®2£© ‘ÃΩæøDM”ÎBNµƒ ˝¡øπÿœµ≤¢÷§√˜£ª
£®3£©»ÙBD£ΩBC£¨MN£Ω2DM£¨µ±AE£Ω![]() ±£¨«ÛOFµƒ≥§£Æ
±£¨«ÛOFµƒ≥§£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø–«∆⁄ÃÏ8£∫00~8£∫30£¨»º∆¯π´Àæ∏¯∆Ω∞≤º”∆¯’浃¥¢∆¯πÞ◊¢»ÎÃÏ»ª∆¯£¨◊¢ÕÍ∆¯∫Û£¨“ªŒªπ§◊˜»À‘±“‘√ø≥µ20√◊![]() µƒº”∆¯¡ø£¨“¿¥Œ∏¯‘⁄º”∆¯’æ≈≈∂”µ»∫Úµƒ»Ù∏…¡æ≥µº”∆¯¥¢∆¯πÞ÷–µƒ¥¢∆¯¡ø
µƒº”∆¯¡ø£¨“¿¥Œ∏¯‘⁄º”∆¯’æ≈≈∂”µ»∫Úµƒ»Ù∏…¡æ≥µº”∆¯¥¢∆¯πÞ÷–µƒ¥¢∆¯¡ø![]() £®√◊
£®√◊![]() £©”Î ±º‰
£©”Î ±º‰![]() £®–° ±£©µƒ∫Ø ˝πÿœµ Ω»ÁÕºÀ˘ æ£∫
£®–° ±£©µƒ∫Ø ˝πÿœµ Ω»ÁÕºÀ˘ æ£∫
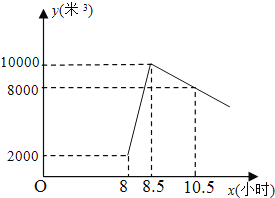
£®1£©8£∫00~8£∫30£¨»º∆¯π´ÀæœÚ¥¢∆¯πÞ◊¢»Î¡À______√◊![]() µƒÃÏ»ª∆¯£ª
µƒÃÏ»ª∆¯£ª
£®2£©µ±![]() ±£¨«Û¥¢∆¯πÞ÷–µƒ¥¢∆¯¡ø£®√◊
±£¨«Û¥¢∆¯πÞ÷–µƒ¥¢∆¯¡ø£®√◊![]() £©”Î ±º‰
£©”Î ±º‰![]() £®–° ±£©µƒ∫Ø ˝πÿœµ Ω£ª
£®–° ±£©µƒ∫Ø ˝πÿœµ Ω£ª
£®3£©’˝‘⁄≈≈∂”µ»∫Úµƒµ⁄20¡æ≥µº”ÕÍ∫Û¥¢∆¯πÞƒ⁄ªπ”–ÃÏ»ª∆¯______√◊![]() £¨’‚20¡æ≥µ‘⁄µ±ÃÏ9£∫00÷Æ«∞ƒÐº”ÕÍ∆¯¬£ø«ÎÀµ√˜¿Ì”…£Æ
£¨’‚20¡æ≥µ‘⁄µ±ÃÏ9£∫00÷Æ«∞ƒÐº”ÕÍ∆¯¬£ø«ÎÀµ√˜¿Ì”…£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø–°√˜–«∆⁄ÃÏ…œŒÁ8£∫00¥”º“≥ˆ∑¢µΩ¿Îº“36«ß√◊µƒ È≥«¬Ú È£¨À˚œ»¥”º“≥ˆ∑¢∆Ôπ´π≤◊‘––≥µµΩπ´Ωª≥µ’棨µ»¡À12∑÷÷”µƒ≥µ£¨»ª∫Û≥Àπ´Ωª≥µ”⁄9£∫48∑÷µΩ¥Ô È≥«£®ºŸ…Ë‘⁄’˚∏ˆπ˝≥Ã÷––°√˜∆Ô≥µµƒÀŸ∂»≤ª±‰£¨π´Ωª≥µ‘»ÀŸ–– ª£¨–°√˜º“°¢π´Ωª≥µ’æ°¢ È≥«“¿¥Œ‘⁄“ªÃı± ÷±µƒπ´¬∑≈‘£©£Æ»ÁÕº «–°√˜¥”º“≥ˆ∑¢¿Îπ´Ωª≥µ’浃¬∑≥Ãy£®«ß√◊£©”ÎÀ˚¥”º“≥ˆ∑¢µƒ ±º‰x£® ±£©÷ƺ‰µƒ∫Ø ˝ÕºœÛ£¨∆‰÷–œþ∂ŒAB∂‘”¶µƒ∫ØΩÃ±Ì¥Ô ΩŒ™y£Ωkx+6£Æ
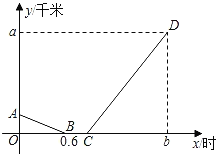
£®1£©«Û–°√˜∆Ôπ´π≤◊‘––≥µµƒÀŸ∂»£ª
£®2£©«Ûœþ∂ŒCD∂‘”¶µƒ∫Ø ˝±Ì¥Ô Ω£ª
£®3£©«Û≥ˆ∑¢ ±º‰x‘⁄ ≤√¥∑∂Œß ±£¨–°√˜¿Îπ´Ωª≥µ’浃¬∑≥Ã≤ª≥¨π˝3«ß√◊£ø
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
π˙º —ß–£”≈—° - ¡∑œ∞≤·¡–±Ì - ‘¡–±Ì
∫˛±± °ª•¡™Õ¯Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®∆Ωî | Õ¯…œ”–∫¶–≈œ¢æŸ±®◊®«¯ | µÁ–≈’©∆≠柱®◊®«¯ | …Ê¿˙ ∑–ÈŒÞ÷˜“”–∫¶–≈œ¢æŸ±®◊®«¯ | …Ê∆Û«÷»®æŸ±®◊®«¯
Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®µÁª∞£∫027-86699610 柱®” œ‰£∫58377363@163.com