
ЁОЬтФПЁПдкбЇЯАЁАжсЖдГЦЯжЯѓЁБФкШнЪБЃЌРЯЪІШУЭЌбЇУЧбАевЩэБпЕФжсЖдГЦЭМаЮЃЌаЁУїРћгУЪжжаЕФвЛИБШ§НЧГпКЭвЛИіСПНЧЦїЃЈШчЭМЫљЪОЃЉНјааЬНОПЃЎ
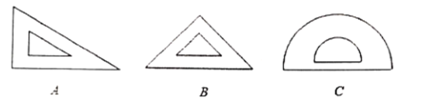
ЃЈ1ЃЉаЁУїдкетШ§МўЮФОпжаШЮШЁвЛМўЃЌНсЙћЪЧжсЖдГЦЭМаЮЕФИХТЪЪЧ_________ЃЛЃЈШЁШ§МўжаШЮвтвЛМўЕФПЩФмадЯрЭЌЃЉ
ЃЈ2ЃЉаЁУїЗЂЯждк![]() ЁЂ
ЁЂ![]() СНАбШ§НЧГпжаИїбЁвЛИіНЧЦДдквЛЦ№ЃЈЮожиЕўЮоЗьЯЖЃЉЛсЕУЕНвЛИіИќДѓЕФНЧЃЌШєУПИіНЧбЁШЁЕФПЩФмадЯрЭЌЃЌЧыгУЛЪїзДЭМЛђСаБэЕФЗНЗЈЫЕУїЦДГЩЕФНЧЪЧЖлНЧЕФИХТЪЪЧЖрЩйЃЎ
СНАбШ§НЧГпжаИїбЁвЛИіНЧЦДдквЛЦ№ЃЈЮожиЕўЮоЗьЯЖЃЉЛсЕУЕНвЛИіИќДѓЕФНЧЃЌШєУПИіНЧбЁШЁЕФПЩФмадЯрЭЌЃЌЧыгУЛЪїзДЭМЛђСаБэЕФЗНЗЈЫЕУїЦДГЩЕФНЧЪЧЖлНЧЕФИХТЪЪЧЖрЩйЃЎ
ЁОД№АИЁПЃЈ1ЃЉ![]() ЃЈ2ЃЉ
ЃЈ2ЃЉ![]()
ЁОНтЮіЁП
ЃЈ1ЃЉевЕНбиФГЬѕжБЯпелЕўЃЌжБЯпСНХдЕФВПЗжФмЙЛЛЅЯржиКЯЕФЭМаЮЪЧжсЖдГЦЭМаЮЃЌХаЖЯГіШ§ИіЭМаЮжажсЖдГЦЭМаЮЕФИіЪ§ЃЌДгЖјПЩЧѓЕУД№АИЃЛ
ЃЈ2ЃЉЛКУЪїзДЭМЃЌИљОнИХТЪЙЋЪНМЦЫуМДПЩНтД№ЃЎ
НтЃКЃЈ1ЃЉвђЮЊЃКЕШбќжБНЧШ§НЧаЮЃЌСПНЧЦїЪЧжсЖдГЦЭМаЮЃЌ
ЫљвдаЁУїдкетШ§МўЮФОпжаШЮШЁвЛМўЃЌНсЙћЪЧжсЖдГЦЭМаЮЕФИХТЪЪЧ![]()
ЙЪД№АИЮЊЃК![]()
ЃЈ2ЃЉЩш90ЁуЕФНЧМДЮЊ![]() ЃЌ60ЁуЕФНЧМЧЮЊ
ЃЌ60ЁуЕФНЧМЧЮЊ![]() ЃЌ45ЁуЕФНЧМЧЮЊ
ЃЌ45ЁуЕФНЧМЧЮЊ![]() ЃЌ30ЁуЕФНЧМЧЮЊ
ЃЌ30ЁуЕФНЧМЧЮЊ![]()
ЛЪїзДЭМШчЭМЫљЪОЃЌ
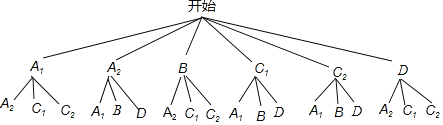
вЛЙВга18жжНсЙћЃЌУПжжНсЙћГіЯжЕФПЩФмадЪЧЯрЭЌЕФЃЌЖјЦфжаПЩвдЦДГЩЕФетИіНЧЪЧЖлНЧЕФНсЙћга12жжЃЌ ЁретИіНЧЪЧЖлНЧЕФИХТЪЪЧ![]()


 ПМЧАБиСЗЯЕСаД№АИ
ПМЧАБиСЗЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌЕуAЕФзјБъЪЧ(2ЃЌ1)ЃЌЕуBЕФзјБъЪЧ(2ЃЌ0) ЃЎзїЕуBЙигкOAЕФЖдГЦЕуBЁфЃЌдђЕуBЁфЕФзјБъЪЧ______ЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
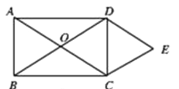
ЁОЬтФПЁПОиаЮABCDЕФЖдНЧЯпЯрНЛгкЕуOЃЎDEЁЮACЃЌCEЁЮBDЃЎ
(1)ЧѓжЄЃКЫФБпаЮOCEDЪЧСтаЮЃЛ
(2)ШєЁЯACBЃН30ЁуЃЌСтаЮOCEDЕФЖјЛ§ЮЊ![]() ЃЌЧѓACЕФГЄЃЎ
ЃЌЧѓACЕФГЄЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГаЁЮЂЦѓвЕЮЊМгПьВњвЕзЊаЭЩ§МЖВНЗЅЃЌв§НјвЛХњAЃЌBСНжжаЭКХЕФЛњЦїЃЎвбжЊвЛЬЈAаЭЛњЦїБШвЛЬЈBаЭЛњЦїУПаЁЪБЖрМгЙЄ2ИіСуМўЃЌЧввЛЬЈAаЭЛњЦїМгЙЄ80ИіСуМўгывЛЬЈBаЭЛњЦїМгЙЄ60ИіСуМўЫљгУЪБМфЯрЕШЃЎ
ЃЈ1ЃЉУПЬЈAЃЌBСНжжаЭКХЕФЛњЦїУПаЁЪБЗжБ№МгЙЄЖрЩйИіСуМўЃП
ЃЈ2ЃЉШчЙћИУЦѓвЕМЦЛЎАВХХAЃЌBСНжжаЭКХЕФЛњЦїЙВ10ЬЈвЛЦ№МгЙЄвЛХњИУСуМўЃЌЮЊСЫШчЦкЭъГЩШЮЮёЃЌвЊЧѓСНжжЛњЦїУПаЁЪБМгЙЄЕФСуМўВЛЩйгк72МўЃЌЭЌЪБЮЊСЫБЃеЯЛњЦїЕФе§ГЃдЫзЊЃЌСНжжЛњЦїУПаЁЪБМгЙЄЕФСуМўВЛФмГЌЙ§76МўЃЌФЧУДAЃЌBСНжжаЭКХЕФЛњЦїПЩвдИїАВХХЖрЩйЬЈЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
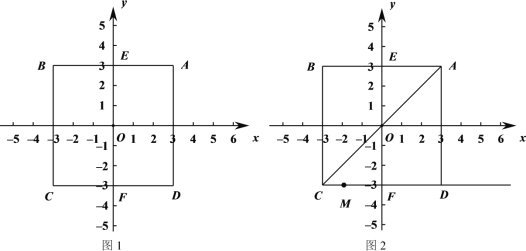
ЁОЬтФПЁПЖдгкЦНУцжБНЧзјБъЯЕxOyжаЕФЕуPКЭЭМаЮNЃЌИјГіШчЯТЖЈвхЃКШчЙћQЮЊЭМаЮNЩЯвЛИіЖЏЕуЃЌPЃЌQСНЕуМфОрРыЕФзюДѓжЕЮЊdmaxЃЌPЃЌQСНЕуМфОрРыЕФзюаЁжЕЮЊdminЃЌЮвУЧАбdmax + dminЕФжЕНаЕуPКЭЭМаЮNМфЕФЁАКЭОрРыЁБЃЌМЧзїdЃЈPЃЌЭМаЮNЃЉЃЎ
ЃЈ1ЃЉШчЭМЃЌе§ЗНаЮABCDЕФжааФЮЊЕуOЃЌA(3ЃЌ3)ЃЎ
Ђй ЕуOЕНЯпЖЮABЕФЁАКЭОрРыЁБdЃЈOЃЌЯпЖЮABЃЉ= ЃЛ
Ђк ЩшИУе§ЗНаЮгыyжсНЛгкЕуEКЭFЃЌЕуPдкЯпЖЮEFЩЯЃЌdЃЈPЃЌе§ЗНаЮABCDЃЉ=7ЃЌЧѓЕуPЕФзјБъЃЎ
ЃЈ2ЃЉШчЭМ2ЃЌдкЃЈ1ЃЉЕФЬѕМўЯТЃЌЙ§CЃЌDСНЕузїЩфЯпCDЃЌСЌНгACЃЌЕуMЪЧЩфЯпCDЩЯЕФвЛЕуЃЌШчЙћ![]() dЃЈMЃЌЯпЖЮADЃЉ
dЃЈMЃЌЯпЖЮADЃЉ![]() ЃЌжБНгаДГіMЕуКсзјБъtШЁжЕЗЖЮЇЃЎ
ЃЌжБНгаДГіMЕуКсзјБъtШЁжЕЗЖЮЇЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЮЪЬтЬсГіЃК
ШчЭМЫљЪОЃЌгаШ§ИљеыКЭЬздквЛИљеыЩЯЕФШєИЩН№ЪєЦЌЃЌАДЯТСаЙцдђЃЌАбН№ЪєЦЌДгвЛИљеыЩЯШЋВПвЦЕНСэвЛИљеыЩЯЃЎ

aЃЎУПДЮжЛФмвЦЖЏ1ИіН№ЪєЦЌЃЛ
bЃЎНЯДѓЕФН№ЪєЦЌВЛФмЗХдкНЯаЁЕФН№ЪєЦЌЩЯУцЃЎ
Аб![]() ИіН№ЪєЦЌДг1КХеывЦЕН3КХеыЃЌзюЩйвЦЖЏЖрЩйДЮЃП
ИіН№ЪєЦЌДг1КХеывЦЕН3КХеыЃЌзюЩйвЦЖЏЖрЩйДЮЃП
ЮЪЬтЬНОПЃКЮЊСЫЬНОПЙцТЩЃЌЮвУЧВЩгУвЛАуЮЪЬтЬиЪтЛЏЕФЗНЗЈЃЌЯШДгМђЕЅЕФЧщаЮШыЪжЃЌдйж№ДЮЕнНјЃЌзюКѓЕУГівЛАуадНсТлЃЎ
ЬНОПвЛЃКЕБ![]() ЪБЃЌжЛашАбН№ЪєЦЌДг1КХеывЦЕН3КХеыЃЌгУЗћКХ
ЪБЃЌжЛашАбН№ЪєЦЌДг1КХеывЦЕН3КХеыЃЌгУЗћКХ![]() БэЪОЃЌЙВвЦЖЏСЫ1ДЮЃЎ
БэЪОЃЌЙВвЦЖЏСЫ1ДЮЃЎ
ЬНОПЖўЃКЕБ![]() ЪБЃЌЮЊСЫБмУтНЋНЯДѓЕФН№ЪєЦЌЗХдкНЯаЁЕФН№ЪєЦЌЩЯУцЃЌЮвУЧРћгУ2КХеызїЮЊЁАжаМфеыЁБЃЌвЦЖЏЕФЫГађЪЧЃК
ЪБЃЌЮЊСЫБмУтНЋНЯДѓЕФН№ЪєЦЌЗХдкНЯаЁЕФН№ЪєЦЌЩЯУцЃЌЮвУЧРћгУ2КХеызїЮЊЁАжаМфеыЁБЃЌвЦЖЏЕФЫГађЪЧЃК
aЃЎАбЕк1ИіН№ЪєЦЌДг1КХеывЦЕН2КХеыЃЛ
bЃЎАбЕк2ИіН№ЪєЦЌДг1КХеывЦЕН3КХеыЃЛ
cЃЎАбЕк1ИіН№ЪєЦЌДг2КХеывЦЕН3КХеыЃЎ
гУЗћКХБэЪОЮЊЃК![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЎЙВвЦЖЏСЫ3ДЮЃЎ
ЃЎЙВвЦЖЏСЫ3ДЮЃЎ
ЬНОПШ§ЃКЕБ![]() ЪБЃЌАбЩЯУцСНИіН№ЪєЦЌзїЮЊвЛИіећЬхЃЌдђЙщНсЮЊ
ЪБЃЌАбЩЯУцСНИіН№ЪєЦЌзїЮЊвЛИіећЬхЃЌдђЙщНсЮЊ![]() ЕФЧщаЮЃЌвЦЖЏЕФЫГађЪЧЃК
ЕФЧщаЮЃЌвЦЖЏЕФЫГађЪЧЃК
aЃЎАбЩЯУцСНИіН№ЪєЦЌДг1КХеывЦЕН2КХеыЃЛ
bЃЎАбЕк3ИіН№ЪєЦЌДг1КХеывЦЕН3КХеыЃЛ
cЃЎАбЩЯУцСНИіН№ЪєЦЌДг2КХеывЦЕН3КХеыЃЎ
ЦфжаЃЈ1ЃЉКЭЃЈ3ЃЉЖМашвЊНшжњжаМфеыЃЌгУЗћКХБэЪОЮЊЃК
![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЎЙВвЦЖЏСЫ7ДЮЃЎ
ЃЎЙВвЦЖЏСЫ7ДЮЃЎ
ЃЈ1ЃЉЬНОПЫФЃКЧыЗТееЧАУцВНжшНјааНтД№ЃКЕБ![]() ЪБЃЌАбЩЯУц3ИіН№ЪєЦЌзїЮЊвЛИіећЬхЃЌвЦЖЏЕФЫГађЪЧЃК___________________________________________________ЃЎ
ЪБЃЌАбЩЯУц3ИіН№ЪєЦЌзїЮЊвЛИіећЬхЃЌвЦЖЏЕФЫГађЪЧЃК___________________________________________________ЃЎ
ЃЈ2ЃЉЬНОПЮхЃКИљОнЩЯУцЕФЙцТЩФуПЩвдЗЂЯжЕБ![]() ЪБЃЌашвЊвЦЖЏ________ДЮЃЎ
ЪБЃЌашвЊвЦЖЏ________ДЮЃЎ
ЃЈ3ЃЉЬНОПСљЃКАб![]() ИіН№ЪєЦЌДг1КХеывЦЕН3КХеыЃЌзюЩйвЦЖЏ________ДЮЃЎ
ИіН№ЪєЦЌДг1КХеывЦЕН3КХеыЃЌзюЩйвЦЖЏ________ДЮЃЎ
ЃЈ4ЃЉЬНОПЦпЃКШчЙћЮвУЧАб![]() ИіН№ЪєЦЌДг1КХеывЦЕН3КХеыЃЌзюЩйвЦЖЏЕФДЮЪ§МЧЮЊ
ИіН№ЪєЦЌДг1КХеывЦЕН3КХеыЃЌзюЩйвЦЖЏЕФДЮЪ§МЧЮЊ![]() ЃЌЕБ
ЃЌЕБ![]() ЪБШчЙћЮвУЧАб
ЪБШчЙћЮвУЧАб![]() ИіН№ЪєЦЌДг1КХеывЦЕН3КХеыЃЌзюЩйвЦЖЏЕФДЮЪ§МЧЮЊ
ИіН№ЪєЦЌДг1КХеывЦЕН3КХеыЃЌзюЩйвЦЖЏЕФДЮЪ§МЧЮЊ![]() ЃЌФЧУД
ЃЌФЧУД![]() гы
гы![]() ЕФЙиЯЕЪЧ
ЕФЙиЯЕЪЧ![]() __________ЃЎ
__________ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
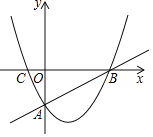
ЁОЬтФПЁПШчЭМЃЌжБЯпyЃН![]() xЉ2гыxжсНЛгкЕуBЃЌгыyжсНЛгкЕуAЃЌХзЮяЯпyЃНax2Љ
xЉ2гыxжсНЛгкЕуBЃЌгыyжсНЛгкЕуAЃЌХзЮяЯпyЃНax2Љ![]() x+cОЙ§AЃЌBСНЕуЃЌгыxжсЕФСэвЛНЛЕуЮЊCЃЎ
x+cОЙ§AЃЌBСНЕуЃЌгыxжсЕФСэвЛНЛЕуЮЊCЃЎ
ЃЈ1ЃЉЧѓХзЮяЯпЕФНтЮіЪНЃЛ
ЃЈ2ЃЉMЮЊХзЮяЯпЩЯвЛЕуЃЌжБЯпAMгыxжсНЛгкЕуNЃЌЕБ![]() ЪБЃЌЧѓЕуMЕФзјБъЃЛ
ЪБЃЌЧѓЕуMЕФзјБъЃЛ
ЃЈ3ЃЉPЮЊХзЮяЯпЩЯЕФЖЏЕуЃЌСЌНгAPЃЌЕБЁЯPABгыЁїAOBЕФвЛИіФкНЧЯрЕШЪБЃЌжБНгаДГіЕуPЕФзјБъЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌХзЮяЯпyЃНax2+bx+cОЙ§ЕуB(4ЃЌ0)ЃЌC(0ЃЌЉ2)ЃЌЖдГЦжсЮЊжБЯпxЃН1ЃЌгыxжсЕФСэвЛИіНЛЕуЮЊЕуAЃЎ
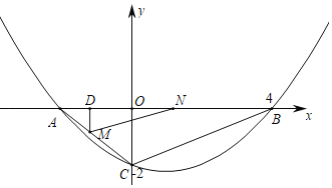
ЃЈ1ЃЉЧѓХзЮяЯпЕФНтЮіЪНЃЛ
ЃЈ2ЃЉЕуMДгЕуAГіЗЂЃЌбиACЯђЕуCдЫЖЏЃЌЫйЖШЮЊ1ИіЕЅЮЛГЄЖШ/УыЃЌЭЌЪБЕуNДгЕуBГіЗЂЃЌбиBAЯђЕуAдЫЖЏЃЌЫйЖШЮЊ2ИіЕЅЮЛГЄЖШ/УыЃЌЕБЕуMЁЂNгавЛЕуЕНДяжеЕуЪБЃЌдЫЖЏЭЃжЙЃЌСЌНгMNЃЌЩшдЫЖЏЪБМфЮЊtУыЃЌЕБtЮЊКЮжЕЪБЃЌAMNЕФУцЛ§SзюДѓЃЌВЂЧѓГіSЕФзюДѓжЕЃЛ
ЃЈ3ЃЉЕуPдкxжсЩЯЃЌЕуQдкХзЮяЯпЩЯЃЌЪЧЗёДцдкЕуPЁЂQЃЌЪЙЕУвдЕуPЁЂQЁЂBЁЂCЮЊЖЅЕуЕФЫФБпаЮЪЧЦНааЫФБпаЮЃЌШєДцдкЃЌжБНгаДГіЫљгаЗћКЯЬѕМўЕФЕуPзјБъЃЌШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
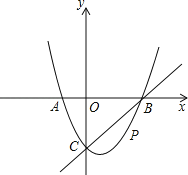
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌЖўДЮКЏЪ§yЃНx2+bx+cЕФЭМЯѓгыxжсНЛгкAЁЂBСНЕуЃЌAЕудкдЕуЕФзѓВрЃЌBЕуЕФзјБъЮЊЃЈ3ЃЌ0ЃЉЃЌгыyжсНЛгкCЃЈ0ЃЌЉ3ЃЉЕуЃЌЕуPЪЧжБЯпBCЯТЗНЕФХзЮяЯпЩЯвЛЖЏЕуЃЎ
ЃЈ1ЃЉЗжБ№ЧѓГіЭМжажБЯпКЭХзЮяЯпЕФКЏЪ§БэДяЪНЃЛ
ЃЈ2ЃЉСЌНгPOЁЂPCЃЌВЂАбЁїPOCбиC OЗелЃЌЕУЕНЫФБпаЮPOPЁфCЃЌФЧУДЪЧЗёДцдкЕуPЃЌЪЙЫФБпаЮPOPЁфCЮЊСтаЮЃПШєДцдкЃЌЧыЧѓГіДЫЪБЕуPЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com