
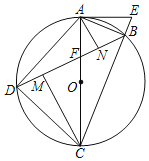
【题目】如图,四边形ABCD内接于⊙O,对角线AC、BD相交于点F,AC是⊙O的直径,延长CB到点E,连接AE,∠BAE=∠ADB,AN⊥BD,CM⊥BD,垂足分别为点N、M.
(1)证明:AE是⊙O的切线;
(2)试探究DM与BN的数量关系并证明;
(3)若BD=BC,MN=2DM,当AE=![]() 时,求OF的长.
时,求OF的长.
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案科目:初中数学 来源: 题型:
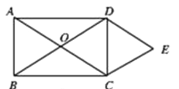
【题目】矩形ABCD的对角线相交于点O.DE∥AC,CE∥BD.
(1)求证:四边形OCED是菱形;
(2)若∠ACB=30°,菱形OCED的而积为![]() ,求AC的长.
,求AC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
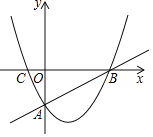
【题目】如图,直线y=![]() x﹣2与x轴交于点B,与y轴交于点A,抛物线y=ax2﹣
x﹣2与x轴交于点B,与y轴交于点A,抛物线y=ax2﹣![]() x+c经过A,B两点,与x轴的另一交点为C.
x+c经过A,B两点,与x轴的另一交点为C.
(1)求抛物线的解析式;
(2)M为抛物线上一点,直线AM与x轴交于点N,当![]() 时,求点M的坐标;
时,求点M的坐标;
(3)P为抛物线上的动点,连接AP,当∠PAB与△AOB的一个内角相等时,直接写出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c经过点B(4,0),C(0,﹣2),对称轴为直线x=1,与x轴的另一个交点为点A.
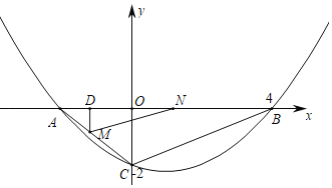
(1)求抛物线的解析式;
(2)点M从点A出发,沿AC向点C运动,速度为1个单位长度/秒,同时点N从点B出发,沿BA向点A运动,速度为2个单位长度/秒,当点M、N有一点到达终点时,运动停止,连接MN,设运动时间为t秒,当t为何值时,AMN的面积S最大,并求出S的最大值;
(3)点P在x轴上,点Q在抛物线上,是否存在点P、Q,使得以点P、Q、B、C为顶点的四边形是平行四边形,若存在,直接写出所有符合条件的点P坐标,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将矩形ABCD沿对角线BD翻折,点A落在点A′处,AD交BC于点E,点F在CD上,连接EF,且CE=3CF,如图1.
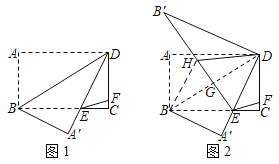
(1)试判断△BDE的形状,并说明理由;
(2)若∠DEF=45°,求tan∠CDE的值;
(3)在(2)的条件下,点G在BD上,且不与B、D两点重合,连接EG并延长到点H,使得EH=BE,连接BH、DH,将△BDH沿DH翻折,点B的对应点B′恰好落在EH的延长线上,如图2.当BH=8时,求GH的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抗击新冠肺炎期间,某小区为方便管理,为居民设计了一个身份识别图案系统:在4×4的正方形网格中,白色正方形表示数字1,黑色正方形表示数字0,将第i行第j列表示的数记为ai,j(其中i,j都是不大于4的正整数),例如,图1中,a1,2=0.对第i行使用公式Ai=ai,1×23+ai,2×22+ai,3×21+ai,4×20进行计算,所得结果A1,A2,A3,A4分别表示居民楼号,单元号,楼层和房间号.例如,图1中,A3=a3,1×23+a3,2×22+a3,3×21+a3,4×20=1×8+0×4+0×2+1×1=9,A4=0×8+0×4+1×2+1×1=3,说明该居民住在9层,3号房间,即903号.
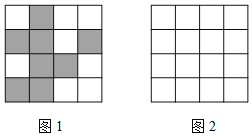
(1)图1中,a1,3= ;
(2)图1代表的居民居住在 号楼 单元;
(3)请仿照图1,在图2中画出8号楼4单元602号居民的身份识别图案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,过⊙T(半径为r)外一点P引它的一条切线,切点为Q,若0<PQ≤2r,则称点P为⊙T的伴随点.
(1)当⊙O的半径为1时,
①在点A(4,0),B(0,![]() ),C(1,
),C(1,![]() )中,⊙O的伴随点是 ;
)中,⊙O的伴随点是 ;
②点D在直线y=x+3上,且点D是⊙O的伴随点,求点D的横坐标d的取值范围;
(2)⊙M的圆心为M(m,0),半径为2,直线y=2x﹣2与x轴,y轴分别交于点E,F.若线段EF上的所有点都是⊙M的伴随点,直接写出m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
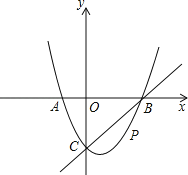
【题目】如图,在平面直角坐标系中,二次函数y=x2+bx+c的图象与x轴交于A、B两点,A点在原点的左侧,B点的坐标为(3,0),与y轴交于C(0,﹣3)点,点P是直线BC下方的抛物线上一动点.
(1)分别求出图中直线和抛物线的函数表达式;
(2)连接PO、PC,并把△POC沿C O翻折,得到四边形POP′C,那么是否存在点P,使四边形POP′C为菱形?若存在,请求出此时点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=ax2+bx+a+2(a≠0)与x轴交于点A(x1,0),点B(x2,0),(点A在点B的左侧),抛物线的对称轴为直线x=-1.
(1)若点A的坐标为(-3,0),求抛物线的表达式及点B的坐标;
(2)C是第三象限的点,且点C的横坐标为-2,若抛物线恰好经过点C,直接写出x2的取值范围;
(3)抛物线的对称轴与x轴交于点D,点P在抛物线上,且∠DOP=45°,若抛物线上满足条件的点P恰有4个,结合图象,求a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com