
【题目】将矩形ABCD沿对角线BD翻折,点A落在点A′处,AD交BC于点E,点F在CD上,连接EF,且CE=3CF,如图1.
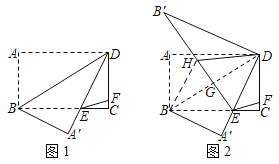
(1)试判断△BDE的形状,并说明理由;
(2)若∠DEF=45°,求tan∠CDE的值;
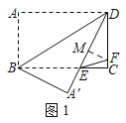
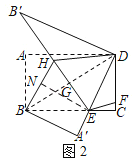
(3)在(2)的条件下,点G在BD上,且不与B、D两点重合,连接EG并延长到点H,使得EH=BE,连接BH、DH,将△BDH沿DH翻折,点B的对应点B′恰好落在EH的延长线上,如图2.当BH=8时,求GH的长.
【答案】(1)△BDE是等腰三角形;理由见解析;(2)tan∠CDE=![]() ;(3)GH=
;(3)GH=![]() .
.
【解析】
(1)根据折叠的性质和平行线的性质得:![]() ,由等角对等边可得
,由等角对等边可得![]() 是等腰三角形;
是等腰三角形;
(2)如图1,过点![]() 作
作![]() 于
于![]() ,根据等腰直角三角形的性质得:
,根据等腰直角三角形的性质得:![]() ,设
,设![]() ,
,![]() ,由勾股定理得
,由勾股定理得![]() ,
,![]() ,设
,设![]() ,根据三角函数定义可得
,根据三角函数定义可得![]() ,最后利用勾股定理列方程可得
,最后利用勾股定理列方程可得![]() 与
与![]() 的关系,从而得结论;
的关系,从而得结论;
(3)如图2,作辅助线,构建全等三角形,证明![]() ,得
,得![]() ,从而由等腰三角形三线合一的性质得
,从而由等腰三角形三线合一的性质得![]() ,证明
,证明![]() ,列比例式可得结论.
,列比例式可得结论.
解:(1)![]() 是等腰三角形,
是等腰三角形,
理由是:如图1,![]() 四边形
四边形![]() 是矩形,
是矩形,
![]() ,
,
![]() ,
,
由折叠得:![]() ,
,
![]() ,
,
![]() ,
,
![]() 是等腰三角形;
是等腰三角形;
(2)如图1,过点![]() 作
作![]() 于
于![]() ,
,
![]() ,
,
![]() ,
,
![]() 四边形
四边形![]() 是矩形,
是矩形,
![]() ,
,
![]() ,
,
![]() 设
设![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
设![]() ,
,
![]()
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,即
,即![]() ,
,
解得:![]() 或
或![]() (舍
(舍![]() ,
,
![]() ;
;
(3)如图2,过点![]() 作
作![]() ,
,
由折叠得:![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,![]() ,
,
![]() ,
,
由(2)知:![]() ,则
,则![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]()
![]() ,
,
![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,D是△ABC内一点,BD⊥CD,E、F、G、H分别是边AB、BD、CD、AC的中点.若AD=10,BD=8,CD=6,则四边形EFGH的周长是( )
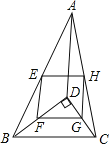
A.24B.20C.12D.10
查看答案和解析>>
科目:初中数学 来源: 题型:
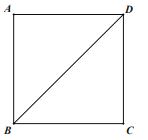
【题目】在正方形ABCD中,E是CD边上的点,过点E作EF⊥BD于F.
(1)尺规作图:在图中求作点E,使得EF=EC;(保留作图痕迹,不写作法)
(2)在(1)的条件下,连接FC,求∠BCF的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
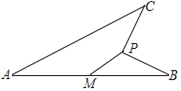
【题目】如图,线段AB=4,M为AB的中点,动点P到点M的距离是1,连接PB,线段PB绕点P逆时针旋转90°得到线段PC,连接AC,则线段AC长度的最大值是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
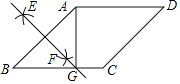
【题目】如图,在菱形ABCD中,按以下步骤作图:
①分别以点A和B为圆心,以大于![]() AB的长为半径作弧,两弧相交于点E、F;
AB的长为半径作弧,两弧相交于点E、F;
②作直线EF交BC于点G,连接AG;若AG⊥BC,CG=3,则AD的长为_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
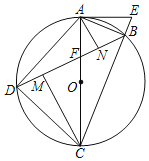
【题目】如图,四边形ABCD内接于⊙O,对角线AC、BD相交于点F,AC是⊙O的直径,延长CB到点E,连接AE,∠BAE=∠ADB,AN⊥BD,CM⊥BD,垂足分别为点N、M.
(1)证明:AE是⊙O的切线;
(2)试探究DM与BN的数量关系并证明;
(3)若BD=BC,MN=2DM,当AE=![]() 时,求OF的长.
时,求OF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解学生居家学习期间对函数知识的掌握情况,某学校数学教师对九年级全体学生进行了一次摸底测试,测试含一次函数、二次函数和反比例函数三项内容,每项满分10分.现随机抽取20名学生的成绩(成绩均为整数)进行收集、整理、描述和分析,下面给出了部分信息:
a.该20名学生一次函数测试成绩如下:7 9 10 9 7 6 8 10 10 8 6 10 10 9 10 9 9 9 10 10
b.该20名学生总成绩和二次函数测试成绩情况统计图:
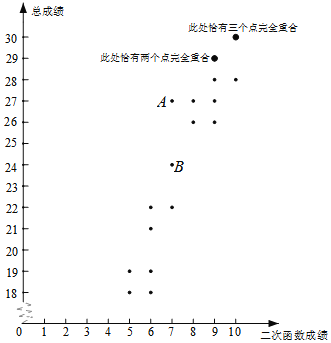
c.该20名学生总成绩平均分为25分,一次函数测试平均分为8.8分.
根据以上信息,回答下列问题:
(1)该20名学生一次函数测试成绩的中位数是 ,众数是 .
(2)若该校九年级共有400名学生,且总成绩不低于26分的学生成绩记为优秀,估计该校九年级本次测试总成绩优秀的约有 人.
(3)在总成绩和二次函数测试成绩情况统计图中,A同学的一次函数测试成绩是 分;若B同学的反比例函数测试成绩是8分,则B同学的一次函数测试成绩是 分.
(4)一次函数、二次函数和反比例函数三项内容中,学生掌握情况最不好的是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】四张大小、形状都相同的卡片上分别写有数字1,2,3,4,把它们放入不透明的盒子中摇匀.
(1)从中随机抽出1张卡片,抽出的卡片上的数字恰好是偶数的概率为 .
(2)从中随机抽出1张卡片,记录数字后放回摇匀,再抽出一张卡片,记录数字.用树状图或列表法求两次抽出的卡片上的数字恰好是两个相邻整数的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】先阅读下列材料,再解答问题.
尺规作图
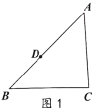
已知:△ABC,D是边AB上一点,如图1,
求作:四边形DBCF,使得四边形DBCF是平行四边形.
小明的做法如下:
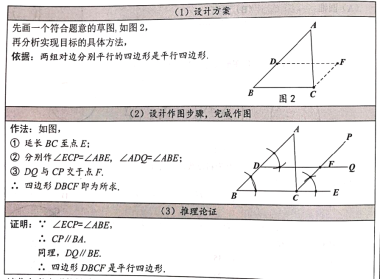
请你参考小明的做法,再设计一一种尺规作图的方法(与小明的方法不同),使得画出的四边形DBCF是平行四边形,并证明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com