
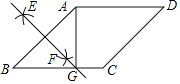
【题目】如图,在菱形ABCD中,按以下步骤作图:
①分别以点A和B为圆心,以大于![]() AB的长为半径作弧,两弧相交于点E、F;
AB的长为半径作弧,两弧相交于点E、F;
②作直线EF交BC于点G,连接AG;若AG⊥BC,CG=3,则AD的长为_______.
科目:初中数学 来源: 题型:
【题目】工厂甲、乙两个部门各有员工400人,为了解这两个部门员工的生产技能情况,进行了抽样调查,请将下列过程补充完整:
收集数据:
从甲、乙两个部门各随机抽取20名员工,进行了生产技能测试,测试成绩(百分制)如下:

整理、描述数据:
按如下分数段整理、描述这两组样本数据:
成绩 人数 部门 | 40≤x≤49 | 50≤x≤59 | 60≤x≤69 | 70≤x≤79 | 80≤x≤89 | 90≤x≤100 |
甲 | 0 | 0 | 1 | 11 | 7 | 1 |
乙 |
(说明:成绩80分及以上为生产技能优秀,70—79分为生产技能良好,60—69分为生产技能合格,60分以下为生产技能不合格)
分析数据:
两组样本数据的平均数、中位数、众数如下表所示:
部门 | 平均数 | 中位数 | 众数 |
甲 | 78.3 | 77.5 | |
乙 | 78 | 81 |
得出结论:
![]() .估计乙部门生产技能优秀的员工人数约为 .
.估计乙部门生产技能优秀的员工人数约为 .
![]() .可以推断出 部门员工的生产技能水平高.理由为 .
.可以推断出 部门员工的生产技能水平高.理由为 .
(至少从两个不同的角度说明推断的合理性)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料:以下是我们教科书中的一段内容,请仔细阅读,并解答有关问题.
公元前3世纪,古希腊学家阿基米德发现:若杠杆上的两物体与支点的距离与其重量成反比,则杠杆平衡,后来人们把它归纳为“杠杆原理”,通俗地说,杠杆原理为:
阻力×阻力臂=动力×动力臂

(问题解决)
若工人师傅欲用撬棍动一块大石头,已知阻力和阻力臂不变,分别为1500N和0.4m.
(1)动力F(N)与动力臂l(m)有怎样的函数关系?当动力臂为1.5m时,撬动石头需要多大的力?
(2)若想使动力F(N)不超过题(1)中所用力的一半,则动力臂至少要加长多少?
(数学思考)
(3)请用数学知识解释:我们使用棍,当阻力与阻力臂一定时,为什么动力臂越长越省力.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,以AB为直径的⊙O交∠BAD的角平分线于C,过C作CD⊥AD于D,交AB的延长线于E.
(1)求证:CD为⊙O的切线.
(2)若![]() ,求cos∠DAB.
,求cos∠DAB.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场销售一批名牌衬衫,平均每天能售出20件,每件盈利40元。经调查发现:如果这种衬衫的售价每降低1元时,平均每天能多售出2件.设每件衬衫降价x元.
(1)降价后,每件衬衫的利润为_____元,销量为_____件;(用含x的式子表示)
(2)为了扩大销售,尽快减少库存,商场决定釆取降价措施。但需要平均每天盈利1200元,求每件衬衫应降价多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将矩形ABCD沿对角线BD翻折,点A落在点A′处,AD交BC于点E,点F在CD上,连接EF,且CE=3CF,如图1.
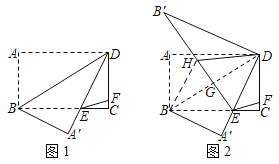
(1)试判断△BDE的形状,并说明理由;
(2)若∠DEF=45°,求tan∠CDE的值;
(3)在(2)的条件下,点G在BD上,且不与B、D两点重合,连接EG并延长到点H,使得EH=BE,连接BH、DH,将△BDH沿DH翻折,点B的对应点B′恰好落在EH的延长线上,如图2.当BH=8时,求GH的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某大学为了解学生在A,B两家餐厅用餐的满意度,从在A,B两家餐厅都用过餐的学生中随机抽取了100人,每人分别对这两家餐厅进行了评分,统计如下:
人数 满意度评分 餐厅 | 非常满意 | 较满意 | 一般 | 不太满意 | 非常不满意 | 合计 |
A | 28 | 40 | 10 | 10 | 12 | 100 |
B | 25 | 20 | 45 | 6 | 4 | 100 |
若小芸要在A,B两家餐厅中选择一家用餐,根据表格中数据,你建议她去_____餐厅(填A或B),理由是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知正方形![]() 中,
中,![]() 为对角线
为对角线![]() 上一点,过点
上一点,过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() ,
,![]() 为
为![]() 的中点,连接
的中点,连接![]() .
.
(1)如图1,求证:![]() ;
;
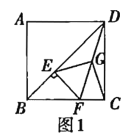
(2)将图1中的![]() 绕点
绕点![]() 逆时针旋转45°,如图2,取
逆时针旋转45°,如图2,取![]() 的中点
的中点![]() ,连接
,连接![]() .问(1)中的结论是否仍然成立?若成立,给出证明;若不成立,请说明理由.
.问(1)中的结论是否仍然成立?若成立,给出证明;若不成立,请说明理由.
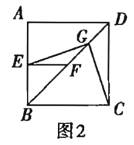
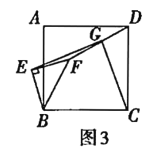
(3)将图1中的![]() 绕点
绕点![]() 逆时计旋转任意角度,如图3,取
逆时计旋转任意角度,如图3,取![]() 的中点
的中点![]() ,连接
,连接![]() .问(1)中的结论是否仍然成立?通过观察你还能得出什么结论?(均不要求证明)
.问(1)中的结论是否仍然成立?通过观察你还能得出什么结论?(均不要求证明)
查看答案和解析>>
科目:初中数学 来源: 题型:
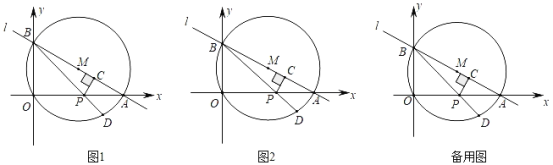
【题目】如图1,直线l:y=﹣![]() x+4与x轴交于点A,与y轴交于点B,以AB为直径作⊙M,点P为线段OA上一动点(与点O、A不重合),作PC⊥AB于C,连结BP并延长交⊙O于点D.
x+4与x轴交于点A,与y轴交于点B,以AB为直径作⊙M,点P为线段OA上一动点(与点O、A不重合),作PC⊥AB于C,连结BP并延长交⊙O于点D.
(1)求点A,B的坐标和tan∠BAO的值;
(2)设![]() =x,tan∠BPO=y.
=x,tan∠BPO=y.
①当x=1时,求y的值及点D的坐标;
②求y关于x的函数表达式;
(3)如图2,连接OC,当点P在线段OA上运动时,求OCPD的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com