
【题目】如图1,直线l:y=﹣![]() x+4与x轴交于点A,与y轴交于点B,以AB为直径作⊙M,点P为线段OA上一动点(与点O、A不重合),作PC⊥AB于C,连结BP并延长交⊙O于点D.
x+4与x轴交于点A,与y轴交于点B,以AB为直径作⊙M,点P为线段OA上一动点(与点O、A不重合),作PC⊥AB于C,连结BP并延长交⊙O于点D.
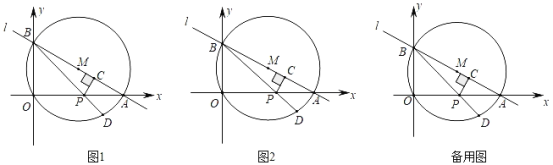
(1)求点A,B的坐标和tan∠BAO的值;
(2)设![]() =x,tan∠BPO=y.
=x,tan∠BPO=y.
①当x=1时,求y的值及点D的坐标;
②求y关于x的函数表达式;
(3)如图2,连接OC,当点P在线段OA上运动时,求OCPD的最大值.
【答案】(1)点A、B的坐标分别为:(8,0)、(0,4);![]() ;(2)①y=
;(2)①y=![]() ,点D的坐标为(
,点D的坐标为(![]() ,﹣
,﹣![]() );②y=
);②y=![]() ;(3)当x=4时,OCPD最大值为
;(3)当x=4时,OCPD最大值为![]()
【解析】
(1)对于直线l:y=﹣![]() x+4,令x=0,则y=4,令y=0,则x=8,求出点A、B的坐标,即可求解;
x+4,令x=0,则y=4,令y=0,则x=8,求出点A、B的坐标,即可求解;
(2)①当x=1时,则BC=AC,PB=PA=![]() ,进而确定直线BP的表达式;根据DM是圆的半径,即可求出点D的坐标;
,进而确定直线BP的表达式;根据DM是圆的半径,即可求出点D的坐标;
②AB=AC+BC,求得PA=![]() ,即可求解;
,即可求解;
(3)证明△OAC∽△ODP,利用二次函数求最大值的方法,即可求解.
解:(1)对于直线l:y=﹣![]() x+4,令x=0,则y=4,令y=0,则x=8,
x+4,令x=0,则y=4,令y=0,则x=8,
故点A、B的坐标分别为:(8,0)、(0,4);
∴tan∠BAO=![]() =
=![]() =
=![]() ;
;
(2)由点A、B的坐标得:AB=![]() =4
=4![]() ,则圆的半径r=2
,则圆的半径r=2![]() ,
,
①如图1,当x=1时,则BC=AC,

又∵PM⊥AB,
∴AM=BM=![]() AB=2/span>
AB=2/span>![]() ,
,
∵tan∠BAO=![]() =
=![]() =
=![]() ,则cos∠BAO=
,则cos∠BAO=![]() ,
,
PB=PA=![]() =
=![]() =5,
=5,
OP=OA﹣AP=8﹣5=3,故点P(3,0),
在Rt△BOP中,y=tan∠BPO=![]() =
=![]() ;
;
设直线BP的表达式为:y=kx+b,则![]() ,解得:
,解得: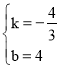 ,
,
故直线BP的表达式为:y=﹣![]() x+4,
x+4,
设点D的坐标为:(m,﹣![]() m+4),
m+4),
∵点M是AB的中点,则其坐标为:(4,2),
∵DM是圆的半径,
∴MD=(m﹣4)2+(﹣![]() m+4﹣2)2=(2
m+4﹣2)2=(2![]() )2,
)2,
解得:m=0或![]() (舍去0),
(舍去0),
故m=![]() ,
,
故点D(![]() ,﹣
,﹣![]() );
);
故y=![]() ,点D的坐标为(
,点D的坐标为(![]() ,﹣
,﹣![]() );
);
②在△Rt△ACP中,AC=![]() =
=![]() PA,
PA,
∵![]() =x,则BC=xAC,
=x,则BC=xAC,
∵AB=AC+BC=![]() PA+
PA+![]() PAx=4
PAx=4![]() ,
,
∴PA=![]() ,
,
∵OP=OA﹣PA=4﹣![]() ,
,
y=tan∠BPO=![]() =
=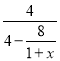 =
=![]() ;
;
(3)如图2,连接OD、OC,
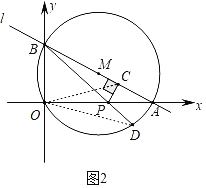
∵∠BOA=90°,∠BCP=90°,
∴O、P、C、B四点共圆,
∴∠COP=∠CBP,
而∠CBP=∠AOD,
∴∠COP=∠AOD,
而∠BDO=∠BAO,
∴△OAC∽△ODP,
∴![]() ,即OCPD=ACOP,
,即OCPD=ACOP,
设PA=x,则OP=8﹣x,
在Rt△ACP中,AC=APcos∠BAO=![]() x=
x=![]() x,
x,
∴OCPD=ACOP=![]() x(8﹣x)=﹣
x(8﹣x)=﹣![]() x2+
x2+![]() x,
x,
∵﹣![]() <0,故OCPD有最大值,
<0,故OCPD有最大值,
当x=4时,OCPD最大值为![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
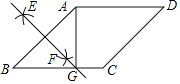
【题目】如图,在菱形ABCD中,按以下步骤作图:
①分别以点A和B为圆心,以大于![]() AB的长为半径作弧,两弧相交于点E、F;
AB的长为半径作弧,两弧相交于点E、F;
②作直线EF交BC于点G,连接AG;若AG⊥BC,CG=3,则AD的长为_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
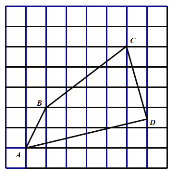
【题目】如图,在每个小正方形的边长为的网格中,点![]() 均在格点上,
均在格点上,![]() 为小正方形边中点.
为小正方形边中点.
(1)![]() 的长等于 ______;
的长等于 ______;
(2)请在如图所示的网格中,用无刻度的直尺,画出一个点![]() ,使其满足
,使其满足![]() 说明点
说明点![]() 的位置是如何找到的(不要求证明)______.
的位置是如何找到的(不要求证明)______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线![]() 为常数,
为常数,![]() )与直线
)与直线![]() 都经过
都经过![]() 两点,
两点,![]() 是该抛物线上的一个动点,过点
是该抛物线上的一个动点,过点![]() 作
作![]() 轴的垂线交直线
轴的垂线交直线![]() 于点
于点![]() ,交x轴于点H.
,交x轴于点H.
(1)求此抛物线和直线![]() 的解析式;
的解析式;
(2)当点![]() 在直线
在直线![]() 下方时,求
下方时,求![]() 取得最大值时点
取得最大值时点![]() 的坐标;
的坐标;
(3)设该抛物线的顶点为![]() 直线
直线![]() 与该抛物线的对称轴交于点
与该抛物线的对称轴交于点![]() .当
.当![]() 以点为顶点的四边形是平行四边形时,求点
以点为顶点的四边形是平行四边形时,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了解学生对“防溺水”安全知识的掌握情况,从全校1500名学生中随机抽取部分学生进行测试,并将测试成绩(百分制,得分均为整数)进行统计分析,绘制了不完整的频数表和频数直方图.
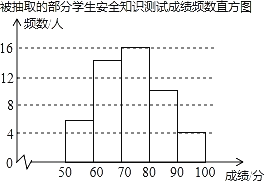
组别 | 成绩x(分) | 频数(人) | 频率 |
A组 | 50≤x<60 | 6 | 0.12 |
B组 | 60≤x<70 | a | 0.28 |
C组 | 70≤x<80 | 16 | 0.32 |
D组 | 80≤x<90 | 10 | 0.20 |
E组 | 90≤x≤100 | 4 | 0.08 |
由图表中给出的信息回答下列问题:
(1)表中的a= ;抽取部分学生的成绩的中位数在 组;
(2)把如图的频数直方图补充完整;
(3)如果成绩达到80分以上(包括80分)为优秀,请估计该校1500名学生中成绩优秀的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】先阅读下列材料,再解答问题.
尺规作图
已知:△ABC,D是边AB上一点,如图1,
求作:四边形DBCF,使得四边形DBCF是平行四边形.
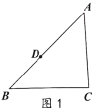
小明的做法如下:
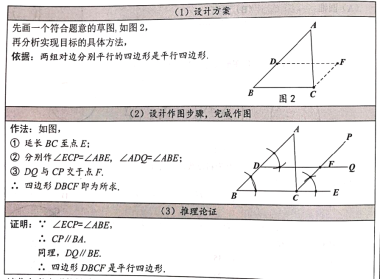
请你参考小明的做法,再设计一一种尺规作图的方法(与小明的方法不同),使得画出的四边形DBCF是平行四边形,并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于平面直角坐标系xOy中的图形W1和图形W2.给出如下定义:在图形W1上存在两点A,B(点A,B可以重合),在图形W2上存在两点M,N,(点M于点N可以重合)使得AM=2BN,则称图形W1和图形W2满足限距关系
(1)如图1,点C(1,0),D(-1,0),E(0,![]() ),点P在线段DE上运动(点P可以与点D,E重合),连接OP,CP.
),点P在线段DE上运动(点P可以与点D,E重合),连接OP,CP.
①线段OP的最小值为_______,最大值为_______;线段CP的取值范直范围是_____;
②在点O,点C中,点____________与线段DE满足限距关系;
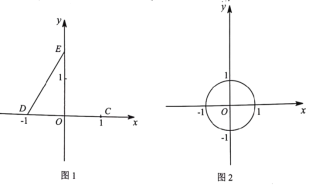
(2)如图2,⊙O的半径为1,直线![]() (b>0)与x轴、y轴分别交于点F,G.若线段FG与⊙O满足限距关系,求b的取值范围;
(b>0)与x轴、y轴分别交于点F,G.若线段FG与⊙O满足限距关系,求b的取值范围;
(3)⊙O的半径为r(r>0),点H,K是⊙O上的两个点,分别以H,K为圆心,1为半径作圆得到⊙H和K,若对于任意点H,K,⊙H和⊙K都满足限距关系,直接写出r的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
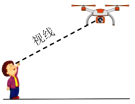
【题目】为做好疫情宣传巡查工作,各地积极借助科技手段加大防控力度.如图,亮亮在外出期间被无人机隔空喊话“戴上口罩,赶紧回家”.据测量,无人机与亮亮的水平距离是15米,当他抬头仰视无人机时,仰角恰好为![]() ,若亮亮身高1.70米,则无人机距离地面的高度约为________米.(结果精确到0.1米,参考数据:
,若亮亮身高1.70米,则无人机距离地面的高度约为________米.(结果精确到0.1米,参考数据:![]() ,
,![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com