
【题目】某校为了解学生对“防溺水”安全知识的掌握情况,从全校1500名学生中随机抽取部分学生进行测试,并将测试成绩(百分制,得分均为整数)进行统计分析,绘制了不完整的频数表和频数直方图.
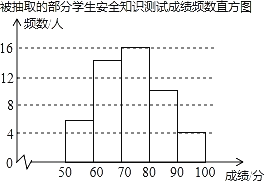
组别 | 成绩x(分) | 频数(人) | 频率 |
A组 | 50≤x<60 | 6 | 0.12 |
B组 | 60≤x<70 | a | 0.28 |
C组 | 70≤x<80 | 16 | 0.32 |
D组 | 80≤x<90 | 10 | 0.20 |
E组 | 90≤x≤100 | 4 | 0.08 |
由图表中给出的信息回答下列问题:
(1)表中的a= ;抽取部分学生的成绩的中位数在 组;
(2)把如图的频数直方图补充完整;
(3)如果成绩达到80分以上(包括80分)为优秀,请估计该校1500名学生中成绩优秀的人数.
科目:初中数学 来源: 题型:
【题目】某商场销售一批名牌衬衫,平均每天能售出20件,每件盈利40元。经调查发现:如果这种衬衫的售价每降低1元时,平均每天能多售出2件.设每件衬衫降价x元.
(1)降价后,每件衬衫的利润为_____元,销量为_____件;(用含x的式子表示)
(2)为了扩大销售,尽快减少库存,商场决定釆取降价措施。但需要平均每天盈利1200元,求每件衬衫应降价多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
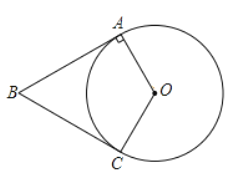
【题目】如图,D为⊙O上一点,点C在直径BA的延长线上,且∠CDA=∠CBD.
(1)求证:CD是⊙O的切线;
(2)若BC=6,tan∠CDA=![]() ,求CD的长.
,求CD的长.
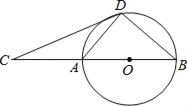
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线![]() 与
与![]() 轴交于点
轴交于点![]() ,交
,交![]() 轴于点
轴于点![]() 的长为
的长为![]() .
.
(1)求抛物线的解析式;
(2)点![]() 是第一象限抛物线上的一点,直线
是第一象限抛物线上的一点,直线![]() 交
交![]() 轴于
轴于![]() ,设点
,设点![]() 的横坐标为
的横坐标为![]() 的长为
的长为![]() ,用含
,用含![]() 的式子表示
的式子表示![]() ;
;
(3)在![]() 的条件下,过点
的条件下,过点![]() 作
作![]() 交
交![]() 轴于点
轴于点![]() ,点
,点![]() 在
在![]() 上,连接
上,连接![]() 交抛物线于点
交抛物线于点![]() ,点
,点![]() 在
在![]() 轴上,
轴上,![]() ,连接
,连接![]()
![]() ,求点
,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】五张完全相同的卡片的正面分别画有等边三角形、平行四边形、矩形、菱形、正方形,将其背面朝上放在桌面上,从中随机抽取一张,所抽取的卡片上的图形既是轴对称图形,又是中心对称图形的概率是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,直线l:y=﹣![]() x+4与x轴交于点A,与y轴交于点B,以AB为直径作⊙M,点P为线段OA上一动点(与点O、A不重合),作PC⊥AB于C,连结BP并延长交⊙O于点D.
x+4与x轴交于点A,与y轴交于点B,以AB为直径作⊙M,点P为线段OA上一动点(与点O、A不重合),作PC⊥AB于C,连结BP并延长交⊙O于点D.
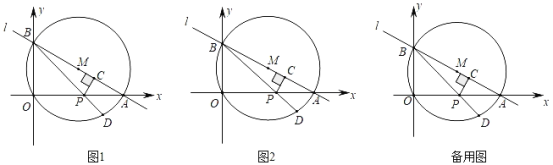
(1)求点A,B的坐标和tan∠BAO的值;
(2)设![]() =x,tan∠BPO=y.
=x,tan∠BPO=y.
①当x=1时,求y的值及点D的坐标;
②求y关于x的函数表达式;
(3)如图2,连接OC,当点P在线段OA上运动时,求OCPD的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形OABC中,![]() .OA=OC, BA=BC.以O为圆心,以OA为半径作☉O
.OA=OC, BA=BC.以O为圆心,以OA为半径作☉O
(1)求证:BC是☉O的切线:
(2)连接BO并延长交⊙O于点D,延长AO交⊙O于点E,与此的延长线交于点F若![]() .
.
①补全图形;
②求证:OF=OB.
查看答案和解析>>
科目:初中数学 来源: 题型:
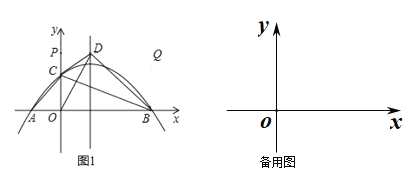
【题目】在平面直角坐标系中,抛物线![]() 与
与![]() 轴交于
轴交于![]() 两点(点
两点(点![]() 在点
在点![]() 左侧),与
左侧),与![]() 轴交于点
轴交于点![]() ,连接
,连接![]() ,将
,将![]() 沿
沿![]() 所在的直线翻折,得到
所在的直线翻折,得到![]() ,连接
,连接![]() .
.
(1)点![]() 的坐标为 ,点
的坐标为 ,点![]() 的坐标为 ;
的坐标为 ;
(2)如图1,若点![]() 落在抛物线的对称轴上,且在
落在抛物线的对称轴上,且在![]() 轴上方,求抛物线的解析式.
轴上方,求抛物线的解析式.
(3)设![]() 的面积为
的面积为![]() ,
,![]() 的面积为
的面积为![]() ,若
,若![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,一次函数![]() 的图象与y轴交于点A,过点
的图象与y轴交于点A,过点![]() ,且平行于x轴的直线与一次函数
,且平行于x轴的直线与一次函数![]() 的图象,反比例函数
的图象,反比例函数![]() 的图象分别交于点C,D.
的图象分别交于点C,D.
(1)求点D 的坐标(用含m的代数式表示);
(2)当m = 1时,用等式表示线段BD与CD长度之间的数量关系,并说明理由;
(3)当BD≤CD时,直接写出m的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com