
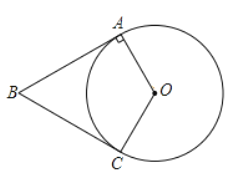
【题目】如图,四边形OABC中,![]() .OA=OC, BA=BC.以O为圆心,以OA为半径作☉O
.OA=OC, BA=BC.以O为圆心,以OA为半径作☉O
(1)求证:BC是☉O的切线:
(2)连接BO并延长交⊙O于点D,延长AO交⊙O于点E,与此的延长线交于点F若![]() .
.
①补全图形;
②求证:OF=OB.
【答案】(1)证明见解析(2)①图见解析(2)证明见解析
【解析】
(1)连接AC,根据等腰三角形的性质得到∠OAC=∠OCA,∠BAC=∠BCA,得到∠OCB=∠OAB=90°,根据切线的判定定理证明;
(2)①根据题意画出图形;
②根据切线长定理得到BA=BC,得到BD是AC的垂直平分线,根据垂径定理、圆心角和弧的关系定理得到∠AOC=120°,根据等腰三角形的判定定理证明结论.
(1)证明:如图1,连接AC,
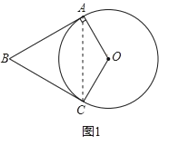
∵OA=OC,
∴∠OAC=∠OCA,
∵BA=BC,
∴∠BAC=∠BCA,
∴∠OAC+∠BCA=∠OCA+∠BCA,即∠OCB=∠OAB=90°,
∴OC⊥BC,
∴BC是⊙O的切线;
(2)①解:补全图形如图2;
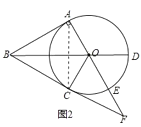
②证明:∵∠OAB=90°,
∴BA是⊙O的切线,又BC是⊙O的切线,
∴BA=BC,
∵BA=BC,OA=OC,
∴BD是AC的垂直平分线,
∴![]() ,
,
∵![]() ,
,
∴![]() =
=![]() ,
,
∴∠AOC=120°,
∴∠AOB=∠COB=∠COE=60°,
∴∠OBF=∠F=30°,
∴OF=OB.


科目:初中数学 来源: 题型:
【题目】2020年春节联欢晚会传承创新亮点多,收视率较往年大幅增长.成都高新区某学校对部分学生就2020年春晚的关注程度,采用随机抽样调査的方式,并根据收集到的信息进行统计,绘制了如图所示的两幅尚不完整的统计图(其中A表示“非常关注”;B表示“关注”;C表示“关注很少”;D表示“不关注”).
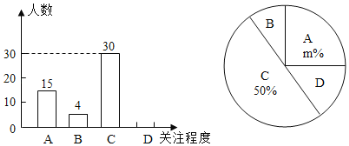
请你根据统计图中所提供的信息解答下列问题:
(1)直接写出m=______;估计该校1800名学生中“不关注”的人数是______人;
(2)在一次交流活动中,老师决定从本次调查回答“关注”的同学中随机选取2名同学来谈谈他们的想法,而本次调查回答“关注”的这些同学中只有一名男同学,请用画树状图或列表的方法求选取到两名同学中刚好有这位男同学的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了解学生对“防溺水”安全知识的掌握情况,从全校1500名学生中随机抽取部分学生进行测试,并将测试成绩(百分制,得分均为整数)进行统计分析,绘制了不完整的频数表和频数直方图.
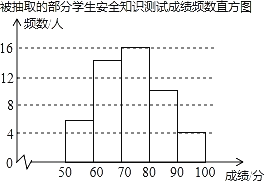
组别 | 成绩x(分) | 频数(人) | 频率 |
A组 | 50≤x<60 | 6 | 0.12 |
B组 | 60≤x<70 | a | 0.28 |
C组 | 70≤x<80 | 16 | 0.32 |
D组 | 80≤x<90 | 10 | 0.20 |
E组 | 90≤x≤100 | 4 | 0.08 |
由图表中给出的信息回答下列问题:
(1)表中的a= ;抽取部分学生的成绩的中位数在 组;
(2)把如图的频数直方图补充完整;
(3)如果成绩达到80分以上(包括80分)为优秀,请估计该校1500名学生中成绩优秀的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,点A,B,C的坐标分别是(0,4),(4,0),(8,0),⊙M是△ABC的外接圆,则点M的坐标为___________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于平面直角坐标系xOy中的图形W1和图形W2.给出如下定义:在图形W1上存在两点A,B(点A,B可以重合),在图形W2上存在两点M,N,(点M于点N可以重合)使得AM=2BN,则称图形W1和图形W2满足限距关系
(1)如图1,点C(1,0),D(-1,0),E(0,![]() ),点P在线段DE上运动(点P可以与点D,E重合),连接OP,CP.
),点P在线段DE上运动(点P可以与点D,E重合),连接OP,CP.
①线段OP的最小值为_______,最大值为_______;线段CP的取值范直范围是_____;
②在点O,点C中,点____________与线段DE满足限距关系;
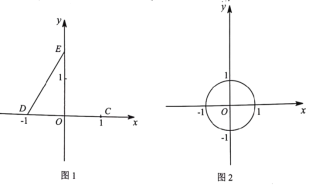
(2)如图2,⊙O的半径为1,直线![]() (b>0)与x轴、y轴分别交于点F,G.若线段FG与⊙O满足限距关系,求b的取值范围;
(b>0)与x轴、y轴分别交于点F,G.若线段FG与⊙O满足限距关系,求b的取值范围;
(3)⊙O的半径为r(r>0),点H,K是⊙O上的两个点,分别以H,K为圆心,1为半径作圆得到⊙H和K,若对于任意点H,K,⊙H和⊙K都满足限距关系,直接写出r的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2017江苏省常州市)为了解某校学生的课余兴趣爱好情况,某调查小组设计了“阅读”、“打球”、“书法”和“其他”四个选项,用随机抽样的方法调查了该校部分学生的课余兴趣爱好情况(每个学生必须选一项且只能选一项),并根据调查结果绘制了如下统计图:

根据统计图所提供的信息,解答下列问题:
(1)本次抽样调查中的样本容量是 ;
(2)补全条形统计图;
(3)该校共有2000名学生,请根据统计结果估计该校课余兴趣爱好为“打球”的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
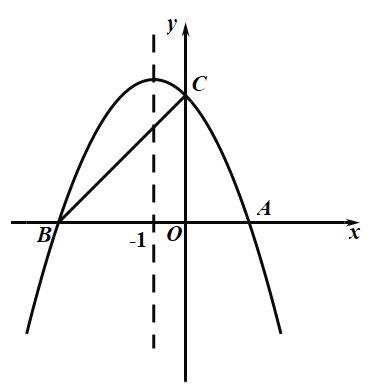
【题目】如图,抛物线![]() 的图象与
的图象与![]() 轴交于
轴交于![]() ,
,![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() ,它的对称轴是直线
,它的对称轴是直线![]() .
.
(1)求抛物线的表达式;
(2)连接![]() ,求线段
,求线段![]() 的长;
的长;
(3)若点![]() 在
在![]() 轴上,且
轴上,且![]() 为等腰三角形,请求出符合条件的所有点
为等腰三角形,请求出符合条件的所有点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知抛物线
中,已知抛物线![]() .
.
(1)抛物线的对称轴为_______;
(2)若当![]() 时,
时,![]() 的最小值是
的最小值是![]() ,求当
,求当![]() 时,
时,![]() 的最大值;
的最大值;
(3)已知直线![]() 与抛物线
与抛物线![]() 存在两个交点,设左侧的交点为点
存在两个交点,设左侧的交点为点![]() ,当
,当![]() 时,求
时,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com