
【题目】如图,D为⊙O上一点,点C在直径BA的延长线上,且∠CDA=∠CBD.
(1)求证:CD是⊙O的切线;
(2)若BC=6,tan∠CDA=![]() ,求CD的长.
,求CD的长.
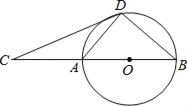
【答案】(1)证明见解析;(2)4.
【解析】
(1)连接OD,如图,先证明∠CDA=∠ODB,再根据圆周角定理得∠ADO+∠ODB=90°,则∠ADO+∠CDA=90°,即∠CDO=90°,于是根据切线的判定定理即可得到结论;
(2)由于∠CDA=∠ODB,则tan∠CDA=tan∠ABD=![]() ,根据正切的定义得到tan∠ABD=
,根据正切的定义得到tan∠ABD=![]() ,接着证明△CAD∽△CDB,由相似的性质得
,接着证明△CAD∽△CDB,由相似的性质得![]() ,然后根据比例的性质可计算出CD的长.
,然后根据比例的性质可计算出CD的长.
详(1)证明:连接OD,如图,
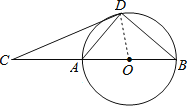
∵OB=OD,
∴∠OBD=∠BDO,
∵∠CDA=∠CBD,
∴∠CDA=∠ODB,
∵AB是⊙O的直径,
∴∠ADB=90°,即∠ADO+∠ODB=90°,
∴∠ADO+∠CDA=90°,
即∠CDO=90°,
∴OD⊥CD,
∴CD是⊙O的切线;
(2)∵∠CDA=∠ODB,
∴tan∠CDA=tan∠ABD=![]() ,
,
在Rt△ABD中,tan∠ABD=![]() ,
,
∵∠DAC=∠BDC,∠CDA=∠CBD,
∴△CAD∽△CDB,
∴![]() ,
,
∴CD=![]() ×6=4.
×6=4.


 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案科目:初中数学 来源: 题型:
【题目】一般情况下![]() 不成立,但有些数对可以使得它成立,例如:a=b=0.我们称使得
不成立,但有些数对可以使得它成立,例如:a=b=0.我们称使得![]() 成立的一对数a,b为“相伴数对”,记为(a,b).
成立的一对数a,b为“相伴数对”,记为(a,b).
(1)若(1,k)是“相伴数对”,求k的值;
(2)直接写出一个“相伴数对”(a0,b0),其中a0≠0,且a0≠1;
(3)若(m,n)是“相伴数对”,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC中,AB=AC=10cm,BC=8cm,点D为AB的中点.如果点P在线段BC上以3cm/s的速度由点B向C点运动,同时,点Q在线段CA上由点C向A点运动.

(1)若点Q的运动速度与点P的运动速度相等,经过1秒后,△BPD与△CQP是否全等,请说明理由.
(2)若点Q的运动速度与点P的运动速度不相等,当点Q的运动速度为多少时,能够使△BPD与△CQP全等?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在下列条件中,不能作为判断△ABD≌△BAC的条件是( )

A. ∠D=∠C,∠BAD=∠ABC B. ∠BAD=∠ABC,∠ABD=∠BAC
C. BD=AC,∠BAD=∠ABC D. AD=BC,BD=AC
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,过B作BE⊥CD,垂足为点E,连接AE,F为AE上一点,且∠BFE=∠C.
(1)求证:△ABF∽△EAD;
(2)若AB=4,∠BAE=30°,求AE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD的顶点A,B在圆上,BC,AD分别与该圆相交于点E,F,G是弧AF的三等分点(弧AG>弧GF),BG交AF于点H.若弧AB的度数为30°,则∠GHF等于( )

A. 40° B. 45° C. 55° D. 80°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公园门票价是每人10元,公园规定:如果一次购票满30张,每张可少收2元.
(1)若某班有18名同学去公园,则需要 元;
(2)若某班有![]() 名同学去公园共需要 元;
名同学去公园共需要 元;
(3)若某班有27名同学去公园,怎样买票更合算?最少需要多少元?
(4)若某班去公园共交费240元,则该班可能有多少人去公园?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,
,![]() 平分
平分![]() 交
交![]() 于点
于点![]() .
.
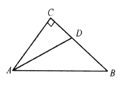
(1)若BC=7,BD=4,则点![]() 到
到![]() 的距离是________;
的距离是________;
(2)若![]() ,点
,点![]() 到
到![]() 的距离是8,则
的距离是8,则![]() 的长是________.
的长是________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com