
����Ŀ���Ķ����ϣ����������ǽ̿����е�һ�����ݣ�����ϸ�Ķ���������й����⣮
��Ԫǰ3���ͣ���ϣ��ѧ�Ұ����·��֣����ܸ��ϵ���������֧��ľ������������ɷ��ȣ���ܸ�ƽ�⣬�������ǰ�������Ϊ���ܸ�ԭ������ͨ��˵���ܸ�ԭ��Ϊ��
������������=������������

����������
������ʦ�������˹���һ���ʯͷ����֪�����������۲��䣬�ֱ�Ϊ1500N��0.4m��
��1������F��N���붯����l��m���������ĺ�����ϵ����������Ϊ1.5mʱ���˶�ʯͷ��Ҫ��������
��2������ʹ����F��N���������⣨1������������һ�룬����������Ҫ�ӳ����٣�
����ѧ˼����
��3��������ѧ֪ʶ���ͣ�����ʹ�ù�����������������һ��ʱ��Ϊʲô������Խ��Խʡ����

���𰸡�400N��1.5�ף�������
��������
����(1)�����ݸܸ˶�����ú����Ľ���ʽ�����l=1.5������Ĵ�С���ɣ�(2)������õĺ�������ʽ���κ���ö����۵Ĵ�С��Ȼ��������ӵij��ȣ�(3)�����÷�����������֪ʶ��ϸܸ˶��ɽ���˵�����ɣ�
���������(1)���������ܸ˶�������FL=1500��0.4�� �������Ľ���ʽΪF=![]() ��
��
��L=1.5ʱ��F=![]() =400�� ��ˣ��˶�ʯͷ��Ҫ400N������
=400�� ��ˣ��˶�ʯͷ��Ҫ400N������
(2)����(1)֪FL=600�� ����������ʽ���Ա�ʾΪ��L=![]() �� ��F=400��
�� ��F=400��![]() =200ʱ��L=3��
=200ʱ��L=3��
3��1.5=1.5��m���� ���������������400N��һ�룬����������Ҫ�ӳ�1.5�ף�
(3)����Ϊ�˹�����ԭ����ѭ���ܸ˶���������������������һ��ʱ����˻�Ϊ����������Ϊk������F�붯����L�ĺ�����ϵʽΪF=![]() �����ݷ��������������ʿ�֪������F�涯����l���������С�����Զ�����Խ��Խʡ����
�����ݷ��������������ʿ�֪������F�涯����l���������С�����Զ�����Խ��Խʡ����


 ��������ܸ�ϰϵ�д�
��������ܸ�ϰϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ھ���ABCD�У��Խ���AC��BD�ཻ�ڵ�O������O��OE��BC��E�㣬����DE��OC��F�㣬��FG��BC��G�㣬����ABC����FGC��λ��ͼ�������ǣ���˵��λ�����ģ���������Ʊȣ������ǣ���˵�����ɣ�
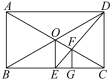
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��O�İ뾶Ϊ10��Բ��O����AB�ľ���Ϊ5������AB���Ե�Բ�ܽǵĶ����ǣ�������
A. 30�� B. 60�� C. 30����150�� D. 60����120��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ���⽻ͨӵ�£�ij����ƻ���һ����ͨ������ͨ��һ���ֵĽ�����ͼ��ʾ(ͼ�е���![]() ��ͨ��
��ͨ��![]() ƽ��)��ͨ��ˮƽ����
ƽ��)��ͨ��ˮƽ����![]() Ϊ8�ף�
Ϊ8�ף� ![]() ��ͨ��б��
��ͨ��б��![]() �ij�Ϊ6�ף�ͨ��б��
�ij�Ϊ6�ף�ͨ��б��![]() ���¶�
���¶�![]() .
.
(1)��ͨ��б��![]() �ij�Ϊ ��;
�ij�Ϊ ��;
(2)Ϊ�����������ߵ����ʶȣ��⽫���ͼ�е�ͨ��б��![]() ���¶ȱ仺���ĺ��ͨ��б��
���¶ȱ仺���ĺ��ͨ��б��![]() ���½�Ϊ30�������ʱ
���½�Ϊ30�������ʱ![]() �ij�.(�����������)
�ij�.(�����������)
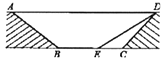
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ,һ��ֱ�����ǰ��ֱ�Ƕ���P���ھ���ABCD��BC����,����ʹһ��ֱ�DZ߾�����D,��һ��ֱ�DZ���AB���ڵ�Q.
��1������д��һ������������,������֤��;
��2����AB=6,BC=8,��PD=3PQʱ,��PC�ij�.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��ó��˾����ij��ˮ���ijɱ�Ϊ20Ԫ/ǧ�ˣ������г����з��֣�����ˮ����δ��48����ۼ�p(Ԫ/ǧ��)��ʱ��t(��)֮��ĺ�������ʽΪ
p��
������������y(kg)��ʱ��t(��)�Ĺ�ϵ���±���
ʱ��t(��) | 1 | 3 | 6 | 10 | 20 | 40 | �� |
��������y(kg) | 118 | 114 | 108 | 100 | 80 | 40 | �� |
(1)��֪y��t֮��ı仯���ɷ���һ�κ�����ϵ�������30������������Ƕ��٣�
(2)�ʣ���һ���������������������������Ϊ���٣�
(3)��ʵ�����۵�ǰ24���У���˾����ÿ����1 kgˮ���;���nԪ����(n��9)��������ƶ�������ַ��֣���ǰ24���У�ÿ��۳��������������������ʱ��t�������������n��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������![]() ��x�ύ��A��B���㣬��ֱ��
��x�ύ��A��B���㣬��ֱ��![]() �ཻ��B��C���㣬����A��C���㡣
�ཻ��B��C���㣬����A��C���㡣
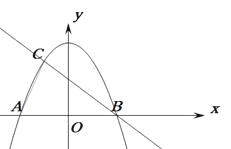
��1��д��ֱ��BC�Ľ���ʽ
��2������ABC�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ij��ҵ����65�����������ס������ֲ�Ʒ��ÿ��ÿ������2����1���ң��ײ�Ʒÿ���ɻ���15Ԫ�������г�������������飬�Ҳ�Ʒÿ�����������5������ÿ������5��ʱ��ÿ���ɻ���120Ԫ��ÿ����1��������ƽ��ÿ����������2Ԫ����ÿ�찲��x�������Ҳ�Ʒ��
��1��������Ϣ���
��Ʒ���� | ÿ�칤�������ˣ� | ÿ����������� | ÿ����Ʒ�ɻ�����Ԫ�� |
�� | 15 | ||
�� |
|
|
��2����ÿ�������ײ�Ʒ�ɻ�õ�����������Ҳ�Ʒ�ɻ�õ������550Ԫ����ÿ���Ҳ�Ʒ�ɻ�õ�����
��3������ҵ�ڲ����ӹ��˵�����£�������������Ʒ��Ҫ��ÿ��ס������ֲ�Ʒ�IJ�����ȣ���֪ÿ��ÿ�������1������ÿ��ÿ��ֻ������һ����Ʒ��������Ʒÿ���ɻ���30Ԫ����ÿ���������ֲ�Ʒ�ɻ�õ�������W��Ԫ�������ֵ����Ӧ��xֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ֱ��y����x��3��y�ύ�ڵ�A���뷴��������y��![]() (k��0)��ͼ���ڵ�C������C��CB��x���ڵ�B��AO��3BO�����������Ľ���ʽΪ( )
(k��0)��ͼ���ڵ�C������C��CB��x���ڵ�B��AO��3BO�����������Ľ���ʽΪ( )

A. y��![]() B. y����
B. y����![]() C. y��
C. y��![]() D. y����
D. y����![]()
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com