
【题目】如图,抛物线![]() 与x轴交于A,B两点,与直线
与x轴交于A,B两点,与直线![]() 相交于B,C两点,连结A,C两点。
相交于B,C两点,连结A,C两点。
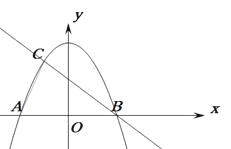
(1)写出直线BC的解析式
(2)求△ABC的面积
【答案】(1)y=-![]() x+
x+![]() ;(2)
;(2)![]() .
.
【解析】
试题(1)利用抛物线,令y=0,解方程求出点A、B的坐标,然后把点B的坐标代入直线BC的解析式求出b的值,即可得解;
(2)根据点A、B的坐标求出AB的长度,再把抛物线解析式与直线BC的解析式联立求解得到点C的坐标,然后根据三角形的面积公式列式计算即可得解;
试题解析:(1)令y=0,则﹣![]() x2+3=0,
x2+3=0,
解得x1=﹣2,x2=2,
所以,点A(﹣2,0),B(2,0),
所以,﹣![]() ×2+b=0,
×2+b=0,
解得b=![]() ,
,
所以,直线BC的解析式为y=﹣![]() x+
x+![]() ;
;
(2)∵点A(﹣2,0),B(2,0),
∴AB=2﹣(﹣2)=2+2=4,
联立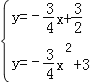 ,
,
解得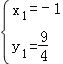 ,
,![]() (为点B坐标,舍去),
(为点B坐标,舍去),
所以,点C的坐标为(﹣1,![]() ),
),
所以,△ABC的面积=![]() ×4×
×4×![]() =
=![]() ;
;


科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,∠A=36°,BD、CE分别是∠ABC、∠BCD的角平分线,则图中的等腰三角形有( )

A. 5个 B. 4个 C. 3个 D. 2个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为响应荆州市“创建全国文明城市”号召,某单位不断美化环境,拟在一块矩形空地上修建绿色植物园,其中一边靠墙,可利用的墙长不超过18m,另外三边由36m长的栅栏围成.设矩形ABCD空地中,垂直于墙的边AB=xm,面积为ym2(如图).
(1)求y与x之间的函数关系式,并写出自变量x的取值范围;
(2)若矩形空地的面积为160m2,求x的值;
(3)若该单位用8600元购买了甲、乙、丙三种绿色植物共400棵(每种植物的单价和每棵栽种的合理用地面积如下表).问丙种植物最多可以购买多少棵?此时,这批植物可以全部栽种到这块空地上吗?请说明理由.
甲 | 乙 | 丙 | |
单价(元/棵) | 14 | 16 | 28 |
合理用地(m2/棵) | 0.4 | 1 | 0.4 |

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料:以下是我们教科书中的一段内容,请仔细阅读,并解答有关问题.
公元前3世纪,古希腊学家阿基米德发现:若杠杆上的两物体与支点的距离与其重量成反比,则杠杆平衡,后来人们把它归纳为“杠杆原理”,通俗地说,杠杆原理为:
阻力×阻力臂=动力×动力臂

(问题解决)
若工人师傅欲用撬棍动一块大石头,已知阻力和阻力臂不变,分别为1500N和0.4m.
(1)动力F(N)与动力臂l(m)有怎样的函数关系?当动力臂为1.5m时,撬动石头需要多大的力?
(2)若想使动力F(N)不超过题(1)中所用力的一半,则动力臂至少要加长多少?
(数学思考)
(3)请用数学知识解释:我们使用棍,当阻力与阻力臂一定时,为什么动力臂越长越省力.

查看答案和解析>>
科目:初中数学 来源: 题型:
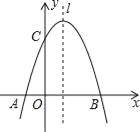
【题目】如图,已知抛物线y=![]() +mx+3与x轴交于A,B两点,与y轴交于点C,点B的坐标为(3,0),
+mx+3与x轴交于A,B两点,与y轴交于点C,点B的坐标为(3,0),
(1)求m的值及抛物线的顶点坐标.
(2)点P是抛物线对称轴l上的一个动点,当PA+PC的值最小时,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
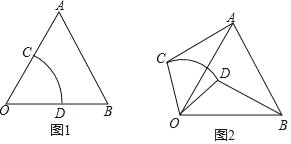
【题目】在等边△AOB中,将扇形COD按图1摆放,使扇形的半径OC、OD分别与OA、OB重合,OA=OB=2,OC=OD=1,固定等边△AOB不动,让扇形COD绕点O逆时针旋转,线段AC、BD也随之变化,设旋转角为α.(0<α≤360°)
(1)当OC∥AB时,旋转角α= 度;
发现:(2)线段AC与BD有何数量关系,请仅就图2给出证明.
应用:(3)当A、C、D三点共线时,求BD的长.
拓展:(4)P是线段AB上任意一点,在扇形COD的旋转过程中,请直接写出线段PC的最大值与最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知在关于x的分式方程![]() ①和一元二次方程(2﹣k)x2+3mx+(3﹣k)n=0②中,k、m、n均为实数,方程①的根为非负数.
①和一元二次方程(2﹣k)x2+3mx+(3﹣k)n=0②中,k、m、n均为实数,方程①的根为非负数.
(1)求k的取值范围;
(2)当方程②有两个整数根x1、x2,k为整数,且k=m+2,n=1时,求方程②的整数根;
(3)当方程②有两个实数根x1、x2,满足x1(x1﹣k)+x2(x2﹣k)=(x1﹣k)(x2﹣k),且k为负整数时,试判断|m|≤2是否成立?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数的图象与抛物线y=-3x2的开口大小和方向都相同,并且在x轴上截得的线段长为3.又知图象过(0,6)点,则该二次函数的表达式为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)的部分图象如图所示,图象过点(﹣1,0),对称轴为直线x=2,下列结论:(1)4a+b=0;(2)9a+c>3b;(3)8a+7b+2c>0;(4)若点A(﹣3,y1)、点B(﹣![]() ,y2)、点C(
,y2)、点C(![]() ,y3)在该函数图象上,则y1<y3<y2;(5)若方程a(x+1)(x﹣5)=﹣3的两根为x1和x2,且x1<x2,则x1<﹣1<5<x2.其中正确的结论有( )
,y3)在该函数图象上,则y1<y3<y2;(5)若方程a(x+1)(x﹣5)=﹣3的两根为x1和x2,且x1<x2,则x1<﹣1<5<x2.其中正确的结论有( )

A. 2个 B. 3个 C. 4个 D. 5个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com