
【题目】已知二次函数的图象与抛物线y=-3x2的开口大小和方向都相同,并且在x轴上截得的线段长为3.又知图象过(0,6)点,则该二次函数的表达式为_____.
科目:初中数学 来源: 题型:
【题目】已知⊙O的半径为10,圆心O到弦AB的距离为5,则弦AB所对的圆周角的度数是( )
A. 30° B. 60° C. 30°或150° D. 60°或120°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】温州某企业安排65名工人生产甲、乙两种产品,每人每天生产2件甲或1件乙,甲产品每件可获利15元.根据市场需求和生产经验,乙产品每天产量不少于5件,当每天生产5件时,每件可获利120元,每增加1件,当天平均每件获利减少2元.设每天安排x人生产乙产品.
(1)根据信息填表
产品种类 | 每天工人数(人) | 每天产量(件) | 每件产品可获利润(元) |
甲 | 15 | ||
乙 |
|
|
(2)若每天生产甲产品可获得的利润比生产乙产品可获得的利润多550元,求每件乙产品可获得的利润.
(3)该企业在不增加工人的情况下,增加生产丙产品,要求每天甲、丙两种产品的产量相等.已知每人每天可生产1件丙(每人每天只能生产一件产品),丙产品每件可获利30元,求每天生产三种产品可获得的总利润W(元)的最大值及相应的x值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象交于点A、B两点,与
的图象交于点A、B两点,与![]() 轴交于点D,过点B作BC⊥
轴交于点D,过点B作BC⊥![]() 轴于点C,点O是线段DC的中点,
轴于点C,点O是线段DC的中点,![]() ,
,![]() .
.
(1)求该反比例函数和一次函数的解析式;
(2)直接写出当![]() 为何值时,
为何值时,![]() ≥
≥![]() .
.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某地特产槟榔芋深受欢迎,某商场以7元/千克收购了3 000千克优质槟榔芋,若现在马上出售,每千克可获得利润3元.根据市场调查发现,近段时间内槟榔芋的售价每天上涨0.2元/千克,为了获得更大利润,商家决定先贮藏一段时间后再出售.根据以往经验,这批槟榔芋的贮藏时间不宜超过100天,在贮藏过程中平均每天损耗约10千克.
(1)若商家将这批槟榔芋贮藏x天后一次性出售,请完成下列表格:
每千克槟榔芋售价 (单位:元) | 可供出售的槟榔芋重量 (单位:千克) | |
现在出售 | 3 000 | |
x天后出售 |
(2)将这批槟榔芋贮藏多少天后一次性出售最终可获得总利润29 000元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=-x+3与y轴交于点A,与反比例函数y=![]() (k≠0)的图象交于点C,过点C作CB⊥x轴于点B,AO=3BO,则反比例函数的解析式为( )
(k≠0)的图象交于点C,过点C作CB⊥x轴于点B,AO=3BO,则反比例函数的解析式为( )

A. y=![]() B. y=-
B. y=-![]() C. y=
C. y=![]() D. y=-
D. y=-![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
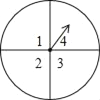
【题目】如图,把一个转盘分成四等份,依次标上数字1、2、3、4,若连续自由转动转盘二次,指针指向的数字分别记作a、b,把a、b作为点A的横、纵坐标.
(1)求点A(a,b)的个数;
(2)求点A(a,b)在函数y=x的图象上的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com