练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】某大学为了解学生在A，B两家餐厅用餐的满意度，从在A，B两家餐厅都用过餐的学生中随机抽取了100人，每人分别对这两家餐厅进行了评分，统计如下：

    人数

    满意度评分

    餐厅

    非常满意

    较满意

    一般

    不太满意

    非常不满意

    合计

    A

    28

    40

    10

    10

    12

    100

    B

    25

    20

    45

    6

    4

    100

    若小芸要在A，B两家餐厅中选择一家用餐，根据表格中数据，你建议她去_____餐厅（填A或B），理由是_____．

    【答案】A 在A餐厅用餐非常满意和较满意的人员比例更大

    【解析】

    根据表格中的数据可知非常满意和较满意的人数A餐厅较多，即可解答本题．

    A餐厅：非常满意和较满意的人数占比为

    B餐厅：非常满意和较满意的人数占比为

    若小芸要在A，B两家餐厅中选择一家用餐，建议她去A餐厅

    理由是：在A餐厅用餐非常满意和较满意的人员比例更大

    故答案为：A，在A餐厅用餐非常满意和较满意的人员比例更大．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，在平面直角标系中，抛物线C：y＝与x轴交于A、B两点（点A在点B的左侧），与y轴交于点C，点D为y轴正半轴上一点．且满足OD＝OC，连接BD，

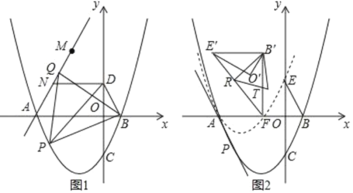
    （1）如图1，点P为抛物线上位于x轴下方一点，连接PB，PD，当S△PBD最大时，连接AP，以PB为边向上作正△BPQ，连接AQ，点M与点N为直线AQ上的两点，MN＝2且点N位于M点下方，连接DN，求DN+MN+AM的最小值

    （2）如图2，在第（1）问的条件下，点C关于x轴的对称点为E，将△BOE绕着点A逆时针旋转60°得到△B′O′E′，将抛物线y＝沿着射线PA方向平移，使得平移后的抛物线C′经过点E，此时抛物线C′与x轴的右交点记为点F，连接E′F，B′F，R为线段E’F上的一点，连接B′R，将△B′E′R沿着B′R翻折后与△B′E′F重合部分记为△B′RT，在平面内找一个点S，使得以B′、R、T、S为顶点的四边形为矩形，求点S的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

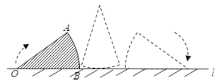
    【题目】如图，在扇形铁皮AOB中，OA=30，∠AOB=36°，OB在直线l上．将此扇形沿l按顺时针方向旋转（旋转过程中无滑动），当OA第一次落在l上时，停止旋转．则点O所经过的路线长为（　　）

    A.B.C.D.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

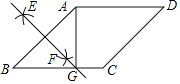
    【题目】如图，在菱形ABCD中，按以下步骤作图：

    ①分别以点A和B为圆心，以大于AB的长为半径作弧，两弧相交于点E、F；

    ②作直线EF交BC于点G，连接AG；若AG⊥BC，CG＝3，则AD的长为_______．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】2020年春节联欢晚会传承创新亮点多，收视率较往年大幅增长．成都高新区某学校对部分学生就2020年春晚的关注程度，采用随机抽样调査的方式，并根据收集到的信息进行统计，绘制了如图所示的两幅尚不完整的统计图（其中A表示“非常关注”；B表示“关注”；C表示“关注很少”；D表示“不关注”）．

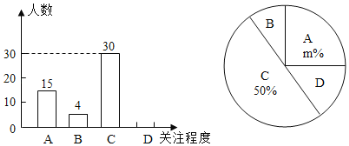
    请你根据统计图中所提供的信息解答下列问题：

    （1）直接写出m＝______；估计该校1800名学生中“不关注”的人数是______人；

    （2）在一次交流活动中，老师决定从本次调查回答“关注”的同学中随机选取2名同学来谈谈他们的想法，而本次调查回答“关注”的这些同学中只有一名男同学，请用画树状图或列表的方法求选取到两名同学中刚好有这位男同学的概率．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】为了解学生居家学习期间对函数知识的掌握情况，某学校数学教师对九年级全体学生进行了一次摸底测试，测试含一次函数、二次函数和反比例函数三项内容，每项满分10分．现随机抽取20名学生的成绩（成绩均为整数）进行收集、整理、描述和分析，下面给出了部分信息：

    a．该20名学生一次函数测试成绩如下：7 9 10 9 7 6 8 10 10 8 6 10 10 9 10 9 9 9 10 10

    b．该20名学生总成绩和二次函数测试成绩情况统计图：

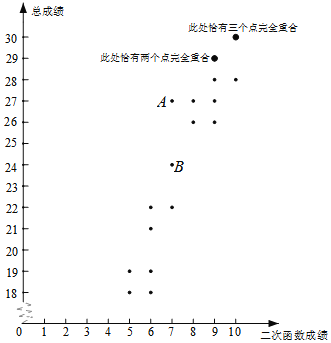
    c．该20名学生总成绩平均分为25分，一次函数测试平均分为8.8分．

    根据以上信息，回答下列问题：

    （1）该20名学生一次函数测试成绩的中位数是　 　，众数是　 　．

    （2）若该校九年级共有400名学生，且总成绩不低于26分的学生成绩记为优秀，估计该校九年级本次测试总成绩优秀的约有　 　人．

    （3）在总成绩和二次函数测试成绩情况统计图中，A同学的一次函数测试成绩是　 　分；若B同学的反比例函数测试成绩是8分，则B同学的一次函数测试成绩是　 　分．

    （4）一次函数、二次函数和反比例函数三项内容中，学生掌握情况最不好的是　 　．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在菱形ABCD中，，AD的垂直平分线交对角线BD于点P，垂足为E，连接CP，则________度．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

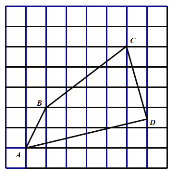
    【题目】如图，在每个小正方形的边长为的网格中，点均在格点上，为小正方形边中点．

    （1）的长等于 ______；

    （2）请在如图所示的网格中，用无刻度的直尺，画出一个点,使其满足说明点的位置是如何找到的(不要求证明)______．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】对于平面直角坐标系xOy中的图形W1和图形W2．给出如下定义：在图形W1上存在两点A，B（点A，B可以重合），在图形W2上存在两点M，N，（点M于点N可以重合）使得AM=2BN，则称图形W1和图形W2满足限距关系

    (1)如图1，点C(1，0)，D(-1，0)，E(0，)，点P在线段DE上运动(点P可以与点D，E重合)，连接OP，CP．

    ①线段OP的最小值为_______，最大值为_______；线段CP的取值范直范围是_____；

    ②在点O，点C中，点____________与线段DE满足限距关系；

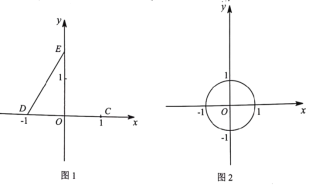
    (2)如图2，⊙O的半径为1，直线(b>0)与x轴、y轴分别交于点F，G．若线段FG与⊙O满足限距关系，求b的取值范围；

    (3)⊙O的半径为r(r>0)，点H，K是⊙O上的两个点，分别以H，K为圆心，1为半径作圆得到⊙H和K，若对于任意点H，K，⊙H和⊙K都满足限距关系，直接写出r的取值范围．

    查看答案和解析>>

    同步练习册答案