
【题目】已知关于![]() 的一元二次方程
的一元二次方程![]()
(1)若方程有实数根,求实数![]() 的取值范围;
的取值范围;
(2)若方程两实数根分别为![]() ,且满足
,且满足![]() ,求实数
,求实数![]() 的值。
的值。
【答案】(1)m≥-1;(2)m=1.
【解析】
(1)根据判别式的意义得到△=[2(m+1)]2-4(m2-1)≥0,然后解不等式即可;(2)根据根与系数的关系得到x1+x2=-(2m+1),x1x2=m2-1,再利用完全平方公式变形![]() ,得到(x1+x2)2-3x1x2-16=0,则[-2(m+1)]2-3(m2-1)-16=0,解方程得m=-9或m=1,然后利用m的取值范围确定满足条件的m的值即可.
,得到(x1+x2)2-3x1x2-16=0,则[-2(m+1)]2-3(m2-1)-16=0,解方程得m=-9或m=1,然后利用m的取值范围确定满足条件的m的值即可.
(1)由题意有△=[2(m+1)]2-4(m2-1)≥0,
整理得8m+8≥0,
解得m≥-1,
∴实数m的取值范围是m≥-1;
(2)由两根关系,得x1+x2=-(2m+1),x1x2=m2-1,
(x1-x2)2=16-x1x2,
(x1+x2)2-3x1x2-16=0,
∴[-2(m+1)]2-3(m2-1)-16=0,
∴m2+8m-9=0,
解得m=-9或m=1,
∵m≥-1,
∴m=1.


 智能训练练测考系列答案
智能训练练测考系列答案科目:初中数学 来源: 题型:
【题目】某企业设计了一款工艺品,每件的成本是![]() 元,为了合理定价,投放市场进行试销.据市场调查,销售单价是
元,为了合理定价,投放市场进行试销.据市场调查,销售单价是![]() 元时,每天的销售量是
元时,每天的销售量是![]() 件,而销售单价每降低
件,而销售单价每降低![]() 元,每天就可多售出
元,每天就可多售出![]() 件,但要求销售单价不得低于成本.求销售单价为多少元时,每天的销售利润最大?最大利润是多少?
件,但要求销售单价不得低于成本.求销售单价为多少元时,每天的销售利润最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场销售一批名牌衬衫,平均每天可售出20件,每件盈利45元,为了扩大销售、增加盈利尽快减少库存,商场决定采取适当的降价措施,经调查发现,如果每件衬衫每降价1元,商场平均每天可多售出4件,若商场平均每天盈利2100元,每件衬衫应降价多少元?请完成下列问题:
(1)未降价之前,某商场衬衫的总盈利为 元.
(2)降价后,设某商场每件衬衫应降价x元,则每件衬衫盈利 元,平均每天可售出 件(用含x的代数式进行表示)
(3)请列出方程,求出x的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AC=BC,∠ACB=90°,D为AB边的中点,以D为直角顶点的Rt△DEF的另两个顶点E,F分别落在边AC,CB(或它们的延长线)上.
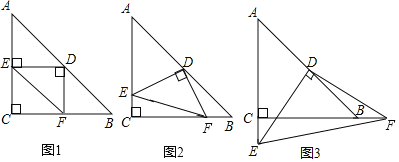
(1)如图1,若Rt△DEF的两条直角边DE,DF与△ABC的两条直角边AC,BC互相垂直,则S△DEF+S△CEF=![]() S△ABC,求当S△DEF=S△CEF=2时,AC边的长;
S△ABC,求当S△DEF=S△CEF=2时,AC边的长;
(2)如图2,若Rt△DEF的两条直角边DE,DF与△ABC的两条直角边AC,BC不垂直,S△DEF+S△CEF=![]() S△ABC,是否成立?若成立,请给予证明;若不成立,请直接写出S△DEF,S△CEF,S△ABC之间的数量关系;
S△ABC,是否成立?若成立,请给予证明;若不成立,请直接写出S△DEF,S△CEF,S△ABC之间的数量关系;
(3)如图3,若Rt△DEF的两条直角边DE,DF与△ABC的两条直角边AC,BC不垂直,且点E在AC的延长线上,点F在CB的延长线上,S△DEF+S△CEF=![]() S△ABC是否成立?若成立,请给予证明;若不成立,请直接写出S△DEF,S△CEF,S△ABC之间的数量关系.
S△ABC是否成立?若成立,请给予证明;若不成立,请直接写出S△DEF,S△CEF,S△ABC之间的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形 ABCD 的对角线 AC 与 BD 相交于点 O,CE∥BD, DE∥AC , AD=2![]() , DE=2,则四边形 OCED 的面积为( )
, DE=2,则四边形 OCED 的面积为( )

A. 2![]() B. 4 C. 4
B. 4 C. 4![]() D. 8
D. 8
查看答案和解析>>
科目:初中数学 来源: 题型:
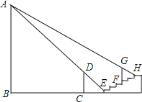
【题目】如图,水平地面上竖立着一盏明亮的路灯![]() ,
,![]() 垂直地面
垂直地面![]() 于
于![]() .旁边有
.旁边有![]() 级台阶.每级台阶高
级台阶.每级台阶高![]() 米,宽
米,宽![]() 米,现有身高
米,现有身高![]() 米的小明垂直站立在离第一级台阶
米的小明垂直站立在离第一级台阶![]() 米的
米的![]() 处时.小明的影子刚好落在第一级台阶的边缘
处时.小明的影子刚好落在第一级台阶的边缘![]() 处.身高
处.身高![]() 米的小华垂直站立在第四级台阶的边缘
米的小华垂直站立在第四级台阶的边缘![]() 处.其影子刚好落在第六级台阶的边缘
处.其影子刚好落在第六级台阶的边缘![]() 处.求路灯
处.求路灯![]() 的高.
的高.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂计划生产甲、乙两种产品共2500吨,每生产1吨甲产品可获得利润0.3万元,每生产1吨乙产品可获得利润0.4万元.设该工厂生产了甲产品x(吨),生产甲、乙两种产品获得的总利润为y(万元).
(1)求y与x之间的函数表达式;
(2)若每生产1吨甲产品需要A原料0.25吨,每生产1吨乙产品需要A原料0.5吨.受市场影响,该厂能获得的A原料至多为1000吨,其它原料充足.求出该工厂生产甲、乙两种产品各为多少吨时,能获得最大利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
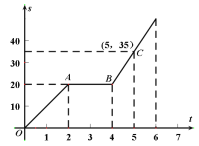
【题目】小明骑自行车从甲地到乙地,图中的折线表示小明行驶的路程![]() 与所用时间
与所用时间![]() 之间的函数关系.试根据函数图像解答下列问题:
之间的函数关系.试根据函数图像解答下列问题:
(1)小明在途中停留了____![]() ,小明在停留之前的速度为____
,小明在停留之前的速度为____![]() ;
;
(2)求线段![]() 的函数表达式;
的函数表达式;
(3)小明出发1小时后,小华也从甲地沿相同路径匀速向乙地骑行,![]()
![]() 时,两人同时到达乙地,求
时,两人同时到达乙地,求![]() 为何值时,两人在途中相遇.
为何值时,两人在途中相遇.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com