
【题目】某工厂计划生产甲、乙两种产品共2500吨,每生产1吨甲产品可获得利润0.3万元,每生产1吨乙产品可获得利润0.4万元.设该工厂生产了甲产品x(吨),生产甲、乙两种产品获得的总利润为y(万元).
(1)求y与x之间的函数表达式;
(2)若每生产1吨甲产品需要A原料0.25吨,每生产1吨乙产品需要A原料0.5吨.受市场影响,该厂能获得的A原料至多为1000吨,其它原料充足.求出该工厂生产甲、乙两种产品各为多少吨时,能获得最大利润.
【答案】(1)![]() ;(2)工厂生产甲产品1000吨,乙产品1500吨时,能获得最大利润.
;(2)工厂生产甲产品1000吨,乙产品1500吨时,能获得最大利润.
【解析】
(1)利润y(元)=生产甲产品的利润+生产乙产品的利润;而生产甲产品的利润=生产1吨甲产品的利润0.3万元×甲产品的吨数x,即0.3x万元,生产乙产品的利润=生产1吨乙产品的利润0.4万元×乙产品的吨数(2500﹣x),即0.4(2500﹣x)万元.
(2)由(1)得y是x的一次函数,根据函数的增减性,结合自变量x的取值范围再确定当x取何值时,利润y最大.
(1)![]() .
.
(2)由题意得:![]() ,解得
,解得![]() .
.
又因为![]() ,所以
,所以![]() .
.
由(1)可知,![]() ,所以
,所以![]() 的值随着
的值随着![]() 的增加而减小.
的增加而减小.
所以当![]() 时,
时,![]() 取最大值,此时生产乙种产品
取最大值,此时生产乙种产品![]() (吨).
(吨).
答:工厂生产甲产品1000吨,乙产品1500吨,时,能获得最大利润.


科目:初中数学 来源: 题型:
【题目】某公司根据市场计划调整投资策略,对![]() ,
,![]() 两种产品进行市场调查,收集数据如表:
两种产品进行市场调查,收集数据如表:
项目 产品 | 年固定成本 (单位:万元) | 每件成本 (单位:万元) | 每件产品销售价 (万元) | 每年最多可生产的件数 |
|
|
|
|
|
|
|
|
|
|
其中![]() 是待定常数,其值是由生产
是待定常数,其值是由生产![]() 的材料的市场价格决定的,变化范围是
的材料的市场价格决定的,变化范围是![]() ,销售
,销售![]() 产品时需缴纳
产品时需缴纳![]() 万元的关税,其中
万元的关税,其中![]() 为生产产品的件数,假定所有产品都能在当年售出,设生产
为生产产品的件数,假定所有产品都能在当年售出,设生产![]() ,
,![]() 两种产品的年利润分别为
两种产品的年利润分别为![]() 、
、![]() (万元),写出
(万元),写出![]() 、
、![]() 与
与![]() 之间的函数关系式,注明其自变量
之间的函数关系式,注明其自变量![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学要印制期末考试卷,甲印刷厂提出:每套试卷收0.6元印刷费,另收400元制版费;乙印刷厂提出:每套试卷收1元印刷费,不再收取制版费.
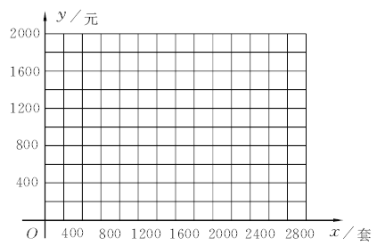
(1)分别写出两个厂的收费y(元)与印刷数量x(套)之间的函数关系式;
(2)请在上面的直角坐标系中分别作出(1)中两个函数的图象;
(3)若学校有学生2000人,为保证每个学生均有试卷,则学校至少要付出印刷费多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 已知,如图边长为2的正方形ABCD中,∠MAN的两边分别交BC、CD边于M、N两点, 且∠MAN=45.

(1)求证:MN=BM+DN.
(2)若AM、AN交对角线BD于E、F两点,设BF=y,DE=x,求y与x的函数关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
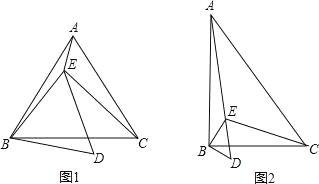
【题目】已知点E在△ABC内,∠ABC=∠EBD=α,∠ACB=∠EDB=60°,∠AEB=150°,∠BEC=90°.
(1)当α=60°时(如图1),
①判断△ABC的形状,并说明理由;
②求证:BD=![]() AE;
AE;
(2)当α=90°时(如图2),求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】等边三角形ABC的边长为6,在AC,BC边上各取一点E,F,连接AF,BE相交于点P.

(1)若AE=CF;
①求证:AF=BE,并求∠APB的度数;
②若AE=2,试求APAF的值;
(2)若AF=BE,当点E从点A运动到点C时,试求点P经过的路径长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,BC是⊙O的切线,切点为B,OC相交于点D,且CD=2,BC=4,
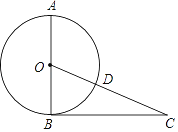
(1)求⊙O的半径;
(2)连接AD并延长,交BC于点E,取BE的中点F,连接DF,试判断DF与⊙O的位置关系,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com