
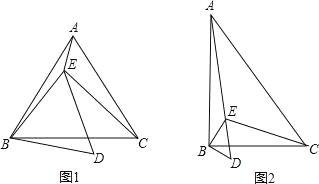
【题目】已知点E在△ABC内,∠ABC=∠EBD=α,∠ACB=∠EDB=60°,∠AEB=150°,∠BEC=90°.
(1)当α=60°时(如图1),
①判断△ABC的形状,并说明理由;
②求证:BD=![]() AE;
AE;
(2)当α=90°时(如图2),求![]() 的值.
的值.
【答案】(1) ①等边三角形;理由见解析; ②证明见解析;(2)
【解析】
试题分析:(1)①由三角形ABC中有两个60°而求得它为等边三角形;②由△EBD也是等边三角形,连接DC,证得△ABE≌△CBD,在直角三角形中很容易证得结论.
(2)连接DC,证得△ABC∽△EBD,设BD=x在Rt△EBD中DE=2x由相似比即得到比值.
试题解析:(1)①判断:△ABC是等边三角形.
理由:∵∠ABC=∠ACB=60°
∴∠BAC=180°-∠ABC-∠ACB=60°=∠ABC=∠ACB
∴△ABC是等边三角形
②证明:同理△EBD也是等边三角形
连接DC,
则AB=BC,BE=BD,∠ABE=60°-∠EBC=∠CBD
∴△ABE≌△CBD
∴AE=CD,∠AEB=∠CDB=150°
∴∠EDC=150°-∠BDE=90°∠CED=∠BEC-∠BED=90°-60°=30°
在Rt△EDC中,![]() ,
,
∴![]() ,即BD=
,即BD=![]() AE.
AE.
(2)连接DC,
∵∠ABC=∠EBD=90°,∠ACB=∠EDB=60°
∴△ABC∽△EBD
∴![]() ,即
,即![]()
又∵∠ABE=90°-∠EBC=∠CBD
∴△ABE∽△CBD,∠AEB=∠CDB=150°,![]()
∴∠EDC=150°-∠BDE=90°∠CED=∠BEC-∠BED=90°-(90°-∠BDE)=60°
设BD=x在Rt△EBD中DE=2x,BE=![]()
在Rt△EDC中CD=DE×tan60°=2![]()
∴![]() ,
,
即![]() .
.


 轻松暑假总复习系列答案
轻松暑假总复习系列答案科目:初中数学 来源: 题型:
【题目】列式计算
(1)-个数与-5的差为-8,求这个数;
(2)-个数与9的差为-5,求这个数.
(3)温度由-9℃上升了3℃后的温度是多少?
(4)甲地的海拔是-63米,乙地比甲地高24米,则乙地的海拔为多少?
(5)土星表面夜间的平均气温为-150℃,白天的平均气温比夜间高27℃,那么白天的平均气温是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
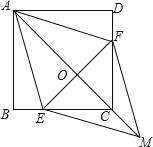
【题目】如图,在正方形ABCD中,点E、F分别在BC和CD上,AE=AF.
(1)求证:CE=CF.
(2)连接AC交EF于点O,延长OC至点M,使OM=OA,连接EM、FM.判断四边形AEMF是什么特殊四边形?并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
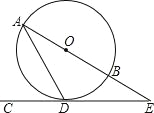
【题目】如图,AB是⊙O的直径,CD是⊙O的切线,切点为D,CD与AB的延长线相交于点E,∠ADC=60°.
(1)求证:△ADE是等腰三角形;
(2)若AD=2![]() ,求BE的长.
,求BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在下列执行异号两数相加的步骤中,错误的是( )
①求两个有理数的绝对值;
②比较两个有理数绝对值的大小;
③将绝对值较大数的符号作为结果的符号;
④将两个有理数绝对值的和作为结果的绝对值
A. ① B. ② C. ③ D. ④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com