
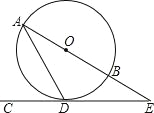
【题目】如图,AB是⊙O的直径,CD是⊙O的切线,切点为D,CD与AB的延长线相交于点E,∠ADC=60°.
(1)求证:△ADE是等腰三角形;
(2)若AD=2![]() ,求BE的长.
,求BE的长.
【答案】(1)证明见解析;(2)2.
【解析】
试题分析:(1)连接OD,根据CD是⊙O的切线,推出∠ODC=90°,求出∠OAD=∠ODA=30°,根据三角形的外角性质求出∠E=∠A,即可得出答案;
(2)由(1)知,DE=DA=2![]() ,根据三角函数的定义求出OD,进一步求出OE,即可得到答案.
,根据三角函数的定义求出OD,进一步求出OE,即可得到答案.
试题解析:(1)连接OD,
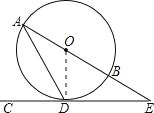
∵CD是⊙O的切线,
∴OD⊥CD,即∠ODC=90°,
∵∠ADC=60°,
∴∠ODA=30°,
在⊙O中OA=OD,
∴∠OAD=∠ODA=30°,
∴∠E=∠ADC-∠EAD=60°-30°=30°=∠EAD,
∴DA=DE,
即△ADE是等腰三角形.
(2)由(1)知,DE=DA=2![]() ,
,
在Rt△ODE中,OD=DE×tan30°=![]() =2,
=2,
OE=2OD=4,
∴BE=OE-OB=OE-OD=4-2=2,
答:BE的长是2.


 教材全解字词句篇系列答案
教材全解字词句篇系列答案科目:初中数学 来源: 题型:
【题目】甲、乙、丙、丁四位同学五次100米跑成绩统计如下表.如果从这四位同学中,选出一位成绩较好且状态稳定的同学参加县运动会,那么应选( )
甲 | 乙 | 丙 | 丁 | |
平均数(秒) | 16 | 15 | 15 | 16 |
方差 | 30 | 30 | 35 | 42 |
A. 甲B. 乙C. 丙D. 丁
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知该抛物线y=x2+bx+c,经过点B(-4,0)和点A(1,0)与y轴交于点C.
(1)确定抛物线的表达式,并求出C点坐标;
(2)如图1,经过点B的直线l交抛物线于点E,且满足∠EBO=∠ACB,求出所有满足条件的点E的坐标,并说明理由;
(3)如图2,M,N是抛物线上的两动点(点M在左,点N在右),分别过点M,N作PM∥x轴,PN∥y轴,PM,PN交于点P.点M,N运动时,且始终保持MN=![]() 不变,当△MNP的面积最大时,请直接写出直线MN的表达式.
不变,当△MNP的面积最大时,请直接写出直线MN的表达式.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将背面完全相同,正面分别写有数字-2、1、-4的三张卡片混合后,小峰从中随机抽取一张,把卡片上的数字作为积的一个因式.将形状、大小完全相同,分别标有数字-1、3、4的三个小球混合后,小华随机抽取一个,把小球上的数字作为积的另一个因式,然后计算这两个数的乘积.
(1)请用列表法或画树状图的方法求出两个数的乘积是非负数的概率.
(2)小峰和小华做游戏,规则是:若这两数的积是非负数,则小峰赢;否则小华赢.你认为这个游戏公平吗?请说明理由,如果不公平,请你修改游戏规则,使游戏公平.
查看答案和解析>>
科目:初中数学 来源: 题型:
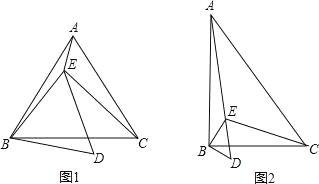
【题目】已知点E在△ABC内,∠ABC=∠EBD=α,∠ACB=∠EDB=60°,∠AEB=150°,∠BEC=90°.
(1)当α=60°时(如图1),
①判断△ABC的形状,并说明理由;
②求证:BD=![]() AE;
AE;
(2)当α=90°时(如图2),求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一元二次方程3x2-2x-1=0的二次项系数、一次项系数、常数项分别为( ).
A.3,2,1 B.-3,2,1 C.3,-2,-1 D.-3,-2,-1
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com