
【题目】已知该抛物线y=x2+bx+c,经过点B(-4,0)和点A(1,0)与y轴交于点C.
(1)确定抛物线的表达式,并求出C点坐标;
(2)如图1,经过点B的直线l交抛物线于点E,且满足∠EBO=∠ACB,求出所有满足条件的点E的坐标,并说明理由;
(3)如图2,M,N是抛物线上的两动点(点M在左,点N在右),分别过点M,N作PM∥x轴,PN∥y轴,PM,PN交于点P.点M,N运动时,且始终保持MN=![]() 不变,当△MNP的面积最大时,请直接写出直线MN的表达式.
不变,当△MNP的面积最大时,请直接写出直线MN的表达式.

【答案】(1)y=x2+3x-4,C点坐标为(0,-4);(2)E1(![]() ,
,![]() ),E2(-
),E2(-![]() ,-
,-![]() );(3)y=x-4或y=-x-
);(3)y=x-4或y=-x-![]() .
.
【解析】
试题分析:(1)根据待定系数法,可得函数解析式,根据自变量与函数值的对应关系,可得答案;
(2)根据勾股定理,可得BC的长,根据等角的正切值相等,可得HO的长,根据待定系数法,可得BE的解析式,根据解方程组,可得E点坐标;
(3)由题意△PMN是等腰直角三角形,得PM=PN=1,设M(a,a2+3a-4)则N(a+1,a2+3a+1)或(a+1,a2+3a-5),代入抛物线的解析式即可求解.
试题解析:(1)y=x2+bx+c,经过点B(-4,0)和点A(1,0),得
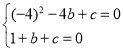 ,解得
,解得![]() ,
,
抛物线的解析式为y=x2+3x-4,
当x=0时,y=-4,
C点坐标为(0,-4);
(2)如图:

由题意,得OB=OC=4,BC=4![]() ,
,
设l1与y轴交于点H,过A作AD⊥BC于点D,△ADB是等腰直角三角形,.
∵AD=BD=ABsin45°=![]() ,CD=
,CD=![]() ,∠ACB=
,∠ACB=![]() .
.
∵∠ACB=∠EBA,
∴HO=![]() ,H(0,
,H(0,![]() ),
),
设直线l1的解析式为y=kx+b,将B、C点坐标代入,得
k=![]() ,
,
l1的解析式为y=![]() x+
x+![]() ,
,
联立抛物线与l1,得![]() x+
x+![]() =x2+3x-4,
=x2+3x-4,
解得x=![]() ,E1(
,E1(![]() ,
,![]() );
);
同理l2:y=-![]() x-
x-![]() ,
,
-![]() x-
x-![]() =x2+3x-4,
=x2+3x-4,
解得x=-![]() ,E2(-
,E2(-![]() ,-
,-![]() ),
),
综上所述:E1(![]() ,
,![]() ),E2(-
),E2(-![]() ,-
,-![]() );
);
(3)∵△PMN是直角三角形,斜边MN=![]() ,
,
∴当△PMN面积最大时,△PMN是等腰直角三角形,PM=PN=1,
由题意设M(a,a2+3a-4)则N(a+1,a2+3a-3)或(a+1,a2+3a-5),
∴a2+3a-3=(a+1)2+3(a+1)-4或a2+3a-5=(a+1)2+3(a+1)-4,
∴a=0或-![]() .
.
①当a=0时,M(0,-4),N(1,-3),设直线MN为y=kx+b,则![]() ,解得
,解得![]() ,所以直线MN为y=x-4.
,所以直线MN为y=x-4.
②当a=-![]() 时,M(-
时,M(-![]() ,-
,-![]() ),N(-
),N(-![]() ,-
,-![]() ),
),
设直线MN为y=k′x+b′,则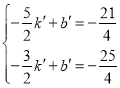 解得
解得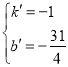 ,
,
所以直线MN为y=-x-![]() .
.


 全能测控期末小状元系列答案
全能测控期末小状元系列答案科目:初中数学 来源: 题型:
【题目】列式计算
(1)-个数与-5的差为-8,求这个数;
(2)-个数与9的差为-5,求这个数.
(3)温度由-9℃上升了3℃后的温度是多少?
(4)甲地的海拔是-63米,乙地比甲地高24米,则乙地的海拔为多少?
(5)土星表面夜间的平均气温为-150℃,白天的平均气温比夜间高27℃,那么白天的平均气温是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某电视台为了解观众对“跑男”综艺节目的喜爱情况,随机抽取某社区部分观众,进行问卷调查,整理绘制了如下不完整的条形统计图和扇形统计图:

请根据以上信息,解答下列问题:
(1)求被调查的男观众中,表示“不喜欢”的男观众所占的百分比是多少?
(2)求这次调查的女观众人数,并直接补全条形统计图.
(3)在扇形统计图中,“一般”所对应的圆心角为 度.
(4)若该社区有女观众约1000人,估计该社区女观众喜欢看“跑男”综艺节目的有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有一组数据为88,96,109,109,122,141,则这组数据的众数和中位数分别是( )
A. 122,109 B. 109,122 C. 109,109 D. 141,109
查看答案和解析>>
科目:初中数学 来源: 题型:
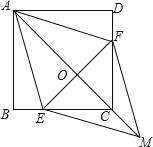
【题目】如图,在正方形ABCD中,点E、F分别在BC和CD上,AE=AF.
(1)求证:CE=CF.
(2)连接AC交EF于点O,延长OC至点M,使OM=OA,连接EM、FM.判断四边形AEMF是什么特殊四边形?并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
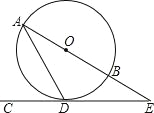
【题目】如图,AB是⊙O的直径,CD是⊙O的切线,切点为D,CD与AB的延长线相交于点E,∠ADC=60°.
(1)求证:△ADE是等腰三角形;
(2)若AD=2![]() ,求BE的长.
,求BE的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com