
【题目】如图,AB是⊙O的直径,BC是⊙O的切线,切点为B,OC相交于点D,且CD=2,BC=4,
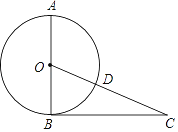
(1)求⊙O的半径;
(2)连接AD并延长,交BC于点E,取BE的中点F,连接DF,试判断DF与⊙O的位置关系,并说明理由.
【答案】(1)3;(2)DF与⊙O相切;理由见解析;
【解析】
(1)设⊙O的半径为R,由切线的性质得出∠OBC=90°,由勾股定理得出方程,解方程即可;
(2)连接BD,由等腰三角形的性质得出∠OBD=∠ODB,由圆周角定理得出∠ADB=90°,求出∠BDE=90°,由直角三角形的性质得出DF=![]() BE=BF,得出∠DBF=∠BDF,证出∠BDF+∠ODB=90°,即可得出结论.
BE=BF,得出∠DBF=∠BDF,证出∠BDF+∠ODB=90°,即可得出结论.
(1)设⊙O的半径为R,
∵BC是⊙O的切线,
∴∠OBC=90°,
∴OB2+BC2=OC2 ,
即R2+42=(R+2)2 ,
解得:R=3,
即⊙O的半径为3
(2)DF与⊙O相切;理由如下: 如图所示:连接BD,
∵OB=OD,
∴∠OBD=∠ODB,
∵AB是⊙O的直径,
∴∠ADB=90°,
∴∠BDE=90°,
∵F是BE的中点,
∴DF=![]() BE=BF,
BE=BF,
∴∠DBF=∠BDF,
∵∠DBF+∠OBD=90°,
∴∠BDF+∠ODB=90°,
∴DF⊥OD,
∴DF与⊙O相切.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】某工厂计划生产甲、乙两种产品共2500吨,每生产1吨甲产品可获得利润0.3万元,每生产1吨乙产品可获得利润0.4万元.设该工厂生产了甲产品x(吨),生产甲、乙两种产品获得的总利润为y(万元).
(1)求y与x之间的函数表达式;
(2)若每生产1吨甲产品需要A原料0.25吨,每生产1吨乙产品需要A原料0.5吨.受市场影响,该厂能获得的A原料至多为1000吨,其它原料充足.求出该工厂生产甲、乙两种产品各为多少吨时,能获得最大利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
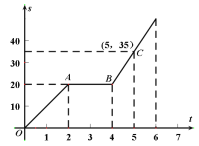
【题目】小明骑自行车从甲地到乙地,图中的折线表示小明行驶的路程![]() 与所用时间
与所用时间![]() 之间的函数关系.试根据函数图像解答下列问题:
之间的函数关系.试根据函数图像解答下列问题:
(1)小明在途中停留了____![]() ,小明在停留之前的速度为____
,小明在停留之前的速度为____![]() ;
;
(2)求线段![]() 的函数表达式;
的函数表达式;
(3)小明出发1小时后,小华也从甲地沿相同路径匀速向乙地骑行,![]()
![]() 时,两人同时到达乙地,求
时,两人同时到达乙地,求![]() 为何值时,两人在途中相遇.
为何值时,两人在途中相遇.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某日上午![]() 点钟,
点钟,![]() 市气象局测得在城市正东方向
市气象局测得在城市正东方向![]() 处
处![]() 点有一台风中心正在以
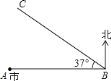
点有一台风中心正在以![]() 千米/时的速度沿西偏北
千米/时的速度沿西偏北![]() 的
的![]() 方向迅速移动(如图所示).据资料表明,在距离台风中心
方向迅速移动(如图所示).据资料表明,在距离台风中心![]() 范围内为严重影响区域(假定台风中心移动方向不变,影响力不变).(参考数据:
范围内为严重影响区域(假定台风中心移动方向不变,影响力不变).(参考数据:![]() ,
,![]() ).
).
(1)![]() 市会不会受这次台风的严重影响,为什么;
市会不会受这次台风的严重影响,为什么;
(2)如果![]() 市会受严重影响,那么这次台风对
市会受严重影响,那么这次台风对![]() 市严重影响多长时间?
市严重影响多长时间?
(3)![]() 市规定台风严重影响前一小时向市民发出预警警报.如果
市规定台风严重影响前一小时向市民发出预警警报.如果![]() 市会受这次台风严重影响,那么
市会受这次台风严重影响,那么![]() 市应在几点钟发出预警警报?
市应在几点钟发出预警警报?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,BD为△ABC的角平分线,且BD=BC,E为BD延长线上的一点,BE=BA,过E作EF⊥AB,F为垂足,下列结论:①△ABD≌△EBC;②∠BCE+∠BCD=180°;③AD=EF=EC;④AE=EC,其中正确的是________(填序号)

查看答案和解析>>
科目:初中数学 来源: 题型:
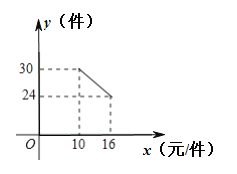
【题目】一名在校大学生利用“互联网+”自主创业,销售一种产品,这种产品成本价10元/件,已知销售价不低于成本价,且物价部门规定这种产品的销售价不高于16元/件,市场调查发现,该产品每天的销售量y(件)与销售价x(元/件)之间的函数关系如图所示.
(1)求y与x之间的函数关系式,并写出自变量x的取值范围;
(2)求每天的销售利润W(元)与销售价x(元/件)之间的函数关系式,并求出每件销售价为多少元时,每天的销售利润最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
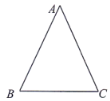
【题目】求证:等腰三角形两腰上的中线相等.
(1)请用尺规作出△ABC两腰上的中线BD、CE(保留痕迹,不写作法);
(2)结合图形,写出已知、求证和证明过程.
查看答案和解析>>
科目:初中数学 来源: 题型:
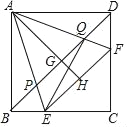
【题目】如图,正方形ABCD的边长为10,点E、F分别在边BC、CD上,且∠EAF=45°,AH⊥EF于点H,AH=10,连接BD,分别交AE、AH、AF于点P、G、Q.
(1)求△CEF的周长;
(2)若E是BC的中点,求证:CF=2DF;
(3)连接QE,求证:AQ=EQ.
查看答案和解析>>
科目:初中数学 来源: 题型:
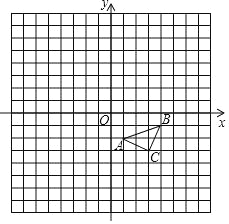
【题目】如图.在平面直角坐标系内,△ABC三个顶点的坐标分别为A(1,﹣2),B(4,﹣1),C(3,﹣3)(正方形网格中,每个小正方形的边长都是1个单位长度).
(1)作出△ABC向左平移5个单位长度,再向下平移3个单位长度得到的△A1B1C1;
(2)以坐标原点O为位似中心,相似比为2,在第二象限内将△ABC放大,放大后得到△A2B2C2作出△A2B2C2;
(3)以坐标原点O为旋转中心,将△ABC逆时针旋转90°,得到△A3B3C3,作出△A3B3C3,并求线段AC扫过的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com