
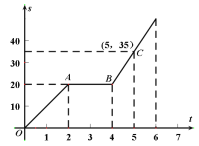
【题目】小明骑自行车从甲地到乙地,图中的折线表示小明行驶的路程![]() 与所用时间
与所用时间![]() 之间的函数关系.试根据函数图像解答下列问题:
之间的函数关系.试根据函数图像解答下列问题:
(1)小明在途中停留了____![]() ,小明在停留之前的速度为____
,小明在停留之前的速度为____![]() ;
;
(2)求线段![]() 的函数表达式;
的函数表达式;
(3)小明出发1小时后,小华也从甲地沿相同路径匀速向乙地骑行,![]()
![]() 时,两人同时到达乙地,求
时,两人同时到达乙地,求![]() 为何值时,两人在途中相遇.
为何值时,两人在途中相遇.
【答案】2; 10;
(2)s=15t-40![]() ;
;
(3)t=3h或t=6h.
【解析】
(1)由图象中的信息可知:小明从第2小时到第4小时行驶的路程没有发生变化,所以途中停留了2![]() ;小明2小时内行驶的路程是20 km,据此可以求出他的速度;
;小明2小时内行驶的路程是20 km,据此可以求出他的速度;
(2)由图象可知:B(4,20),C(5,35),设线段![]() 的函数表达式为s=kt+b,代入后得到方程组,解方程组即可;
的函数表达式为s=kt+b,代入后得到方程组,解方程组即可;
(3)先求出从甲地到乙地的总路程,现求小华的速度,然后分三种情况讨论两人在途中相遇问题.当![]() 时, 10t=10(t-1);当
时, 10t=10(t-1);当![]() 时, 20=10(t-1);当
时, 20=10(t-1);当![]() 时, 15t-40=10(t-1);逐一求解即可.
时, 15t-40=10(t-1);逐一求解即可.
解:(1)由图象可知:小明从第2小时到第4小时行驶的路程没有发生变化,所以途中停留了2![]() ;
;
由图象可知:小明2小时内行驶的路程是20 km,
所以他的速度是![]() (km/ h);
(km/ h);
故答案是:2;10.
(2)设线段![]() 的函数表达式为s=kt+b,
的函数表达式为s=kt+b,
由图象可知:B(4,20),C(5,35),
∴![]() ,
,
∴![]() ,
,
∴线段![]() 的函数表达式为s=15t-40
的函数表达式为s=15t-40![]() ;
;
(3)在s=15t-40中,当t=6时,s=15×6-40=50,
∴从甲地到乙地全程为50 km,
∴小华的速度=![]() (km/ h),
(km/ h),
下面分三种情况讨论两人在途中相遇问题:
当![]() 时,两人在途中相遇,则
时,两人在途中相遇,则
10t=10(t-1),方程无解,不合题意,舍去;
当![]() 时,两人在途中相遇,则
时,两人在途中相遇,则
20=10(t-1),解得t=3;
当![]() 时,两人在途中相遇,则
时,两人在途中相遇,则
15t-40=10(t-1),解得t=6;
∴综上所述,当t=3h或t=6h时,两人在途中相遇.


科目:初中数学 来源: 题型:
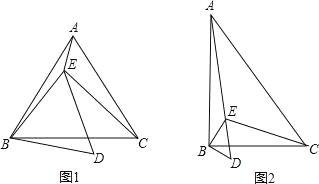
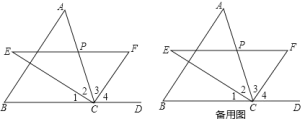
【题目】已知点E在△ABC内,∠ABC=∠EBD=α,∠ACB=∠EDB=60°,∠AEB=150°,∠BEC=90°.
(1)当α=60°时(如图1),
①判断△ABC的形状,并说明理由;
②求证:BD=![]() AE;
AE;
(2)当α=90°时(如图2),求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】等边三角形ABC的边长为6,在AC,BC边上各取一点E,F,连接AF,BE相交于点P.

(1)若AE=CF;
①求证:AF=BE,并求∠APB的度数;
②若AE=2,试求APAF的值;
(2)若AF=BE,当点E从点A运动到点C时,试求点P经过的路径长.
查看答案和解析>>
科目:初中数学 来源: 题型:
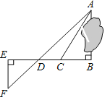
【题目】为了测量被池塘隔开的![]() 、
、![]() 两点之间的距离,根据实际情况,作出如图所示的图形,其中
两点之间的距离,根据实际情况,作出如图所示的图形,其中![]() ,
,![]() ,
,![]() 交
交![]() 于
于![]() ,
,![]() 在
在![]() 上.有四位同学分别测量出以下四组数据:①
上.有四位同学分别测量出以下四组数据:①![]() ,
,![]() ; ②
; ②![]() ,
,![]() ,
,![]() ;③
;③![]() ,
,![]() ,
,![]() ;④
;④![]() ,
,![]() ,
,![]() .根据所测数据,能出
.根据所测数据,能出![]() ,
,![]() 间距离的有________(填上所有能求出
间距离的有________(填上所有能求出![]() 、
、![]() 间距离的序号)
间距离的序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形![]() 是由两个小正方形和两个小长方形组成的,根据图形解答下列问题:
是由两个小正方形和两个小长方形组成的,根据图形解答下列问题:
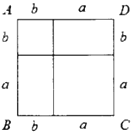
(1)请用两种不同的方法表示正方形![]() 的面积,并写成一个等式;
的面积,并写成一个等式;
(2)运用(1)中的等式,解决以下问题:
①已知![]() ,
,![]() ,求
,求![]() 的值;
的值;
②已知![]() ,
,![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,BC是⊙O的切线,切点为B,OC相交于点D,且CD=2,BC=4,
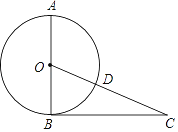
(1)求⊙O的半径;
(2)连接AD并延长,交BC于点E,取BE的中点F,连接DF,试判断DF与⊙O的位置关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 中,点
中,点![]() 是
是![]() 边上一个动点,过
边上一个动点,过![]() 作直线
作直线![]() ,交
,交![]() 的平分线于点
的平分线于点![]() ,交
,交![]() 的外角
的外角![]() 平分线于点
平分线于点![]() .
.
![]() 请说明:
请说明:![]() ;
;
![]() 当点
当点![]() 在
在![]() 边上运动到何处时,四边形
边上运动到何处时,四边形![]() 是矩形?为什么?
是矩形?为什么?
![]() 在
在![]() 的条件下,
的条件下,![]() 满足什么条件时,四边形
满足什么条件时,四边形![]() 是正方形?为什么?
是正方形?为什么?
![]() 当点
当点![]() 在边
在边![]() 上运动时,四边形
上运动时,四边形![]() 可能是菱形吗?请说明理由.
可能是菱形吗?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com