
【题目】如图,正方形![]() 是由两个小正方形和两个小长方形组成的,根据图形解答下列问题:
是由两个小正方形和两个小长方形组成的,根据图形解答下列问题:
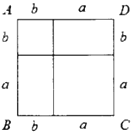
(1)请用两种不同的方法表示正方形![]() 的面积,并写成一个等式;
的面积,并写成一个等式;
(2)运用(1)中的等式,解决以下问题:
①已知![]() ,
,![]() ,求
,求![]() 的值;
的值;
②已知![]() ,
,![]() ,求
,求![]() 的值.
的值.
科目:初中数学 来源: 题型:
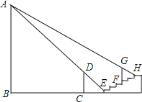
【题目】如图,水平地面上竖立着一盏明亮的路灯![]() ,
,![]() 垂直地面
垂直地面![]() 于
于![]() .旁边有
.旁边有![]() 级台阶.每级台阶高
级台阶.每级台阶高![]() 米,宽
米,宽![]() 米,现有身高
米,现有身高![]() 米的小明垂直站立在离第一级台阶
米的小明垂直站立在离第一级台阶![]() 米的
米的![]() 处时.小明的影子刚好落在第一级台阶的边缘
处时.小明的影子刚好落在第一级台阶的边缘![]() 处.身高
处.身高![]() 米的小华垂直站立在第四级台阶的边缘
米的小华垂直站立在第四级台阶的边缘![]() 处.其影子刚好落在第六级台阶的边缘
处.其影子刚好落在第六级台阶的边缘![]() 处.求路灯
处.求路灯![]() 的高.
的高.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,点D、E、F分别在AB、BC、AC上,且∠ADF+∠DEC=180°,∠AFE=∠BDE.
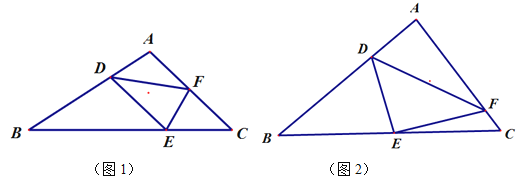
(1)如图1,当DE=DF时,图1中是否存在于AB相等的线段?若存在,请找出并加以证明.若不存在说明理由.
(2)如图2,当DE=kDF(其中0<k<1)时,若∠A=90°,AF=m,求BD的长(用含k,m的式子表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
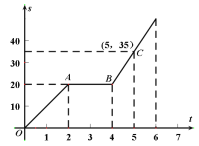
【题目】小明骑自行车从甲地到乙地,图中的折线表示小明行驶的路程![]() 与所用时间
与所用时间![]() 之间的函数关系.试根据函数图像解答下列问题:
之间的函数关系.试根据函数图像解答下列问题:
(1)小明在途中停留了____![]() ,小明在停留之前的速度为____
,小明在停留之前的速度为____![]() ;
;
(2)求线段![]() 的函数表达式;
的函数表达式;
(3)小明出发1小时后,小华也从甲地沿相同路径匀速向乙地骑行,![]()
![]() 时,两人同时到达乙地,求
时,两人同时到达乙地,求![]() 为何值时,两人在途中相遇.
为何值时,两人在途中相遇.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市每天都用360元从批发商城批发甲乙两种型号“垃圾分类”垃圾桶进行零售,批发价和零售价如下表所示:
批发价(元个) | 零售价(元/个) | |
甲型号垃圾桶 | 12 | 16 |
乙型号垃圾桶 | 30 | 36 |
若设该超市每天批发甲型号“垃圾分类”垃圾桶x个,乙型号“垃圾分类”垃圾桶y个,
(1)求y关于x的函数表达式.
(2)若某天该超市老板想将两种型号的“垃圾分类”垃圾桶全部售完后,所获利润率不低于30%,则该超市至少批发甲型号“垃圾分类”垃圾桶多少个?(利润率=利润/成本).
查看答案和解析>>
科目:初中数学 来源: 题型:
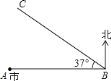
【题目】某日上午![]() 点钟,
点钟,![]() 市气象局测得在城市正东方向
市气象局测得在城市正东方向![]() 处
处![]() 点有一台风中心正在以
点有一台风中心正在以![]() 千米/时的速度沿西偏北
千米/时的速度沿西偏北![]() 的
的![]() 方向迅速移动(如图所示).据资料表明,在距离台风中心
方向迅速移动(如图所示).据资料表明,在距离台风中心![]() 范围内为严重影响区域(假定台风中心移动方向不变,影响力不变).(参考数据:
范围内为严重影响区域(假定台风中心移动方向不变,影响力不变).(参考数据:![]() ,
,![]() ).
).
(1)![]() 市会不会受这次台风的严重影响,为什么;
市会不会受这次台风的严重影响,为什么;
(2)如果![]() 市会受严重影响,那么这次台风对
市会受严重影响,那么这次台风对![]() 市严重影响多长时间?
市严重影响多长时间?
(3)![]() 市规定台风严重影响前一小时向市民发出预警警报.如果
市规定台风严重影响前一小时向市民发出预警警报.如果![]() 市会受这次台风严重影响,那么
市会受这次台风严重影响,那么![]() 市应在几点钟发出预警警报?
市应在几点钟发出预警警报?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,BD为△ABC的角平分线,且BD=BC,E为BD延长线上的一点,BE=BA,过E作EF⊥AB,F为垂足,下列结论:①△ABD≌△EBC;②∠BCE+∠BCD=180°;③AD=EF=EC;④AE=EC,其中正确的是________(填序号)

查看答案和解析>>
科目:初中数学 来源: 题型:
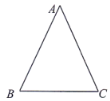
【题目】求证:等腰三角形两腰上的中线相等.
(1)请用尺规作出△ABC两腰上的中线BD、CE(保留痕迹,不写作法);
(2)结合图形,写出已知、求证和证明过程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,E、F分别是边AD、CD上的点,AE=ED,DF=![]() DC,连接EF并延长交BC的延长线于点G.
DC,连接EF并延长交BC的延长线于点G.
(1)求证:△ABE∽△DEF;
(2)若正方形的边长为4,求BG的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com