
【题目】如图,在△ABC中,点D、E、F分别在AB、BC、AC上,且∠ADF+∠DEC=180°,∠AFE=∠BDE.
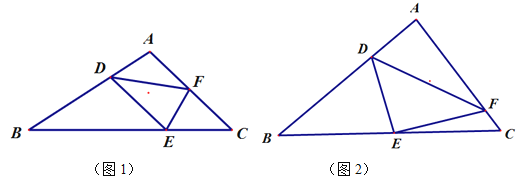
(1)如图1,当DE=DF时,图1中是否存在于AB相等的线段?若存在,请找出并加以证明.若不存在说明理由.
(2)如图2,当DE=kDF(其中0<k<1)时,若∠A=90°,AF=m,求BD的长(用含k,m的式子表示).
【答案】(1)存在,AB=BE,理由见解析;(2)BD= ;
;
【解析】试题(1)存在,AB=BE,理由如下:
延长BA、EF交于点G,连接AE,由已知可得∠EDG=∠AFG,又∠G=∠G为公共角,从而可得△GAF∽△GED,所以![]() ,又∠G=∠G,从而可得△GAE∽△GFD,所以有∠ADF=∠AEF,由∠ADF+∠DEC=180°,∠DEC+∠BED=180°,可得∠AEF=∠DEB,从而得∠BEA=∠DEF,由于DE=DF,可得∠DEF=∠DFE,从而可得∠DAE=∠BEA,继而得AB=EB;
,又∠G=∠G,从而可得△GAE∽△GFD,所以有∠ADF=∠AEF,由∠ADF+∠DEC=180°,∠DEC+∠BED=180°,可得∠AEF=∠DEB,从而得∠BEA=∠DEF,由于DE=DF,可得∠DEF=∠DFE,从而可得∠DAE=∠BEA,继而得AB=EB;
(2)连接AE,由(1)知,∠AEF=∠DEB,∠AFE=∠BDE,从而可得△EDB∽△EFA,继而可得![]() ,∠B=∠EAF,由∠BAC=90°,从而可得∴∠AEB=90°继而可得∠DEF=90°,由DE=kDF,可得EF=
,∠B=∠EAF,由∠BAC=90°,从而可得∴∠AEB=90°继而可得∠DEF=90°,由DE=kDF,可得EF=![]() DF,从而可得BD=
DF,从而可得BD= .
.
试题解析:(1)存在,AB=BE,理由如下:
延长BA、EF交于点G,连接AE,∵∠BDE+∠EDG=180°,∠AFE+∠AFG=180°,∠AFE=∠BDE,∴∠EDG=∠AFG,又∵∠G=∠G,∴△GAF∽△GED,∴![]() ,又∵∠G=∠G,∴△GAE∽△GFD,∴∠ADF=∠AEF,∵∠ADF+∠DEC=180°,∠DEC+∠BED=180°,∴∠AEF=∠DEB,∴∠BEA=∠DEF,∵DE=DF,∴∠DEF=∠DFE,∵∠DAE=∠G+∠AEF,∠DFE=∠G+∠ADF,∴∠DAE=∠BEA,∴AB=EB;
,又∵∠G=∠G,∴△GAE∽△GFD,∴∠ADF=∠AEF,∵∠ADF+∠DEC=180°,∠DEC+∠BED=180°,∴∠AEF=∠DEB,∴∠BEA=∠DEF,∵DE=DF,∴∠DEF=∠DFE,∵∠DAE=∠G+∠AEF,∠DFE=∠G+∠ADF,∴∠DAE=∠BEA,∴AB=EB;
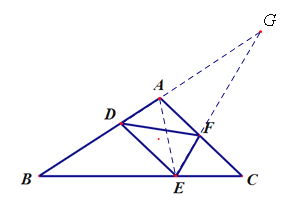
(2)连接AE,由(1)知,∠AEF=∠DEB,∠AFE=∠BDE,∴△EDB∽△EFA,∴![]() ,∠B=∠EAF,∵∠BAE+∠EAF=∠BAC=90°,∴∠B+∠BAE=90°,∴∠AEB=90°,即∠BED+∠AED=90°,∴∠AED+∠AEF=90°,即∠DEF=90°,∴EF2=DF2-DE2,∵DE=kDF,∴EF=
,∠B=∠EAF,∵∠BAE+∠EAF=∠BAC=90°,∴∠B+∠BAE=90°,∴∠AEB=90°,即∠BED+∠AED=90°,∴∠AED+∠AEF=90°,即∠DEF=90°,∴EF2=DF2-DE2,∵DE=kDF,∴EF=![]() DF,∴
DF,∴ ,即
,即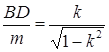 ,∴BD=
,∴BD=


科目:初中数学 来源: 题型:
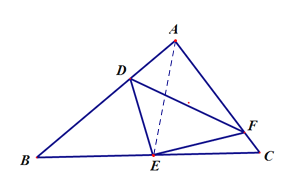
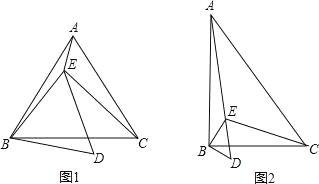
【题目】已知点E在△ABC内,∠ABC=∠EBD=α,∠ACB=∠EDB=60°,∠AEB=150°,∠BEC=90°.
(1)当α=60°时(如图1),
①判断△ABC的形状,并说明理由;
②求证:BD=![]() AE;
AE;
(2)当α=90°时(如图2),求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
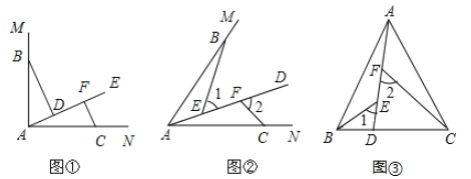
【题目】(1)如图①,![]() ,射线
,射线![]() 在这个角的内部,点
在这个角的内部,点![]() 、
、![]() 分别在
分别在![]() 的边
的边![]() 、
、![]() 上,且
上,且![]() ,
,![]() 于点
于点![]() ,
,![]() 于点
于点![]() .求证:
.求证:![]() ;
;
(2)如图②,点![]() 、
、![]() 分别在
分别在![]() 的边
的边![]() 、
、![]() 上,点
上,点![]() 、
、![]() 都在
都在![]() 内部的射线
内部的射线![]() 上,
上,![]() 、
、![]() 分别是
分别是![]() 、
、![]() 的外角.已知
的外角.已知![]() ,且
,且![]() .求证:
.求证:![]() ;
;
(3)如图③,在![]() 中,
中,![]() ,
,![]() .点
.点![]() 在边
在边![]() 上,
上,![]() ,点
,点![]() 、
、![]() 在线段
在线段![]() 上,
上,![]() .若
.若![]() 的面积为15,求
的面积为15,求![]() 与
与![]() 的面积之和.
的面积之和.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】等边三角形ABC的边长为6,在AC,BC边上各取一点E,F,连接AF,BE相交于点P.

(1)若AE=CF;
①求证:AF=BE,并求∠APB的度数;
②若AE=2,试求APAF的值;
(2)若AF=BE,当点E从点A运动到点C时,试求点P经过的路径长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形![]() 是由两个小正方形和两个小长方形组成的,根据图形解答下列问题:
是由两个小正方形和两个小长方形组成的,根据图形解答下列问题:
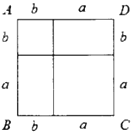
(1)请用两种不同的方法表示正方形![]() 的面积,并写成一个等式;
的面积,并写成一个等式;
(2)运用(1)中的等式,解决以下问题:
①已知![]() ,
,![]() ,求
,求![]() 的值;
的值;
②已知![]() ,
,![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
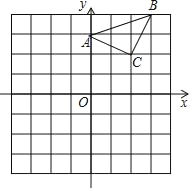
【题目】已知:△ABC在直角坐标平面内,三个顶点的坐标分别为A(0,3)、B(3,4)、C(2,2)(正方形网格中每个小正方形的边长是一个单位长度).
(1)画出△ABC向下平移4个单位长度得到的△A1B1C1,点C1的坐标是 ;
(2)以点B为位似中心,在网格内画出△A2B2C2,使△A2B2C2与△ABC位似,且位似比为2:1,点C2的坐标是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com