
【题目】关于![]() 的方程
的方程![]() 有两个不相等的实数根
有两个不相等的实数根![]() ,
,![]() .
.
![]() 求
求![]() 的取值范围.
的取值范围.
![]() 若
若![]() ,试说明此方程有两个负根.
,试说明此方程有两个负根.
![]() 在
在![]() 的条件下,若
的条件下,若![]() ,求
,求![]() 的值.
的值.
【答案】(1)![]() ;(2)详见解析;(3)
;(2)详见解析;(3)![]() .
.
【解析】
(1)根据判别式的意义得到△=4(k-1)2-4k2>0,然后解不等式即可;
(2)根据根与系数的关系得到x1+x2=2(k-1),x1x2=k2,由于k<![]() ,k≠0,所以x1+x2=2(k-1)<0,x1x2=k2>0,然后根据有理数乘法的运算性质得到x1,x2都为负数;
,k≠0,所以x1+x2=2(k-1)<0,x1x2=k2>0,然后根据有理数乘法的运算性质得到x1,x2都为负数;
(3)先根据x1,x2都为负数,去绝对值得到-x1+x2=4,两边平方后变形得到(x1+x2)2-4x1x2=16,则4(k-1)2-4k2=16,然后解方程即可.
(1)根据题意得![]() ,
,
解得![]() ;
;
(2)∵![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,![]() 都为负数,即此方程有两个负根;
都为负数,即此方程有两个负根;
(3)∵![]() ,
,![]() 都为负数,
都为负数,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】在一款名为超级玛丽的游戏中,玛丽到达一个高为10米的高台A,利用旗杆顶部的绳索,划过90°到达与高台A水平距离为17米,高为3米的矮台B,求旗杆的高度OM和玛丽在荡绳索过程中离地面的最低点的高度MN.

查看答案和解析>>
科目:初中数学 来源: 题型:
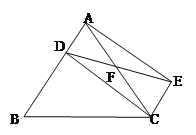
【题目】如图,D是△ABC的边AB上一点,CE∥AB,DE交AC于点F,若FA=FC.
(1)求证:四边形ADCE是平行四边形;
(2)若AE⊥EC,EF=EC=1,求四边形ADCE的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某企业设计了一款工艺品,每件的成本是![]() 元,为了合理定价,投放市场进行试销.据市场调查,销售单价是
元,为了合理定价,投放市场进行试销.据市场调查,销售单价是![]() 元时,每天的销售量是
元时,每天的销售量是![]() 件,而销售单价每降低
件,而销售单价每降低![]() 元,每天就可多售出
元,每天就可多售出![]() 件,但要求销售单价不得低于成本.求销售单价为多少元时,每天的销售利润最大?最大利润是多少?
件,但要求销售单价不得低于成本.求销售单价为多少元时,每天的销售利润最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
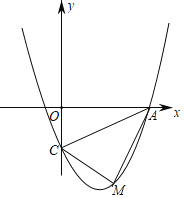
【题目】如图,抛物线经过点A(4,0)、B(﹣2,0)、C(0,﹣4)
(1)求抛物线的解析式;
(2)在抛物线AC段上是否存在点M,使△ACM的面积为3,求出在此时M的坐标,若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场销售一批名牌衬衫,平均每天可售出20件,每件盈利45元,为了扩大销售、增加盈利尽快减少库存,商场决定采取适当的降价措施,经调查发现,如果每件衬衫每降价1元,商场平均每天可多售出4件,若商场平均每天盈利2100元,每件衬衫应降价多少元?请完成下列问题:
(1)未降价之前,某商场衬衫的总盈利为 元.
(2)降价后,设某商场每件衬衫应降价x元,则每件衬衫盈利 元,平均每天可售出 件(用含x的代数式进行表示)
(3)请列出方程,求出x的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AC=BC,∠ACB=90°,D为AB边的中点,以D为直角顶点的Rt△DEF的另两个顶点E,F分别落在边AC,CB(或它们的延长线)上.
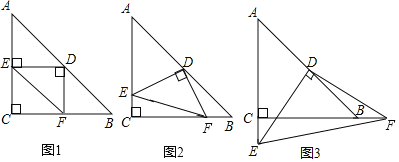
(1)如图1,若Rt△DEF的两条直角边DE,DF与△ABC的两条直角边AC,BC互相垂直,则S△DEF+S△CEF=![]() S△ABC,求当S△DEF=S△CEF=2时,AC边的长;
S△ABC,求当S△DEF=S△CEF=2时,AC边的长;
(2)如图2,若Rt△DEF的两条直角边DE,DF与△ABC的两条直角边AC,BC不垂直,S△DEF+S△CEF=![]() S△ABC,是否成立?若成立,请给予证明;若不成立,请直接写出S△DEF,S△CEF,S△ABC之间的数量关系;
S△ABC,是否成立?若成立,请给予证明;若不成立,请直接写出S△DEF,S△CEF,S△ABC之间的数量关系;
(3)如图3,若Rt△DEF的两条直角边DE,DF与△ABC的两条直角边AC,BC不垂直,且点E在AC的延长线上,点F在CB的延长线上,S△DEF+S△CEF=![]() S△ABC是否成立?若成立,请给予证明;若不成立,请直接写出S△DEF,S△CEF,S△ABC之间的数量关系.
S△ABC是否成立?若成立,请给予证明;若不成立,请直接写出S△DEF,S△CEF,S△ABC之间的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
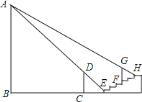
【题目】如图,水平地面上竖立着一盏明亮的路灯![]() ,
,![]() 垂直地面
垂直地面![]() 于
于![]() .旁边有
.旁边有![]() 级台阶.每级台阶高
级台阶.每级台阶高![]() 米,宽
米,宽![]() 米,现有身高
米,现有身高![]() 米的小明垂直站立在离第一级台阶
米的小明垂直站立在离第一级台阶![]() 米的
米的![]() 处时.小明的影子刚好落在第一级台阶的边缘
处时.小明的影子刚好落在第一级台阶的边缘![]() 处.身高
处.身高![]() 米的小华垂直站立在第四级台阶的边缘
米的小华垂直站立在第四级台阶的边缘![]() 处.其影子刚好落在第六级台阶的边缘
处.其影子刚好落在第六级台阶的边缘![]() 处.求路灯
处.求路灯![]() 的高.
的高.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,点D、E、F分别在AB、BC、AC上,且∠ADF+∠DEC=180°,∠AFE=∠BDE.
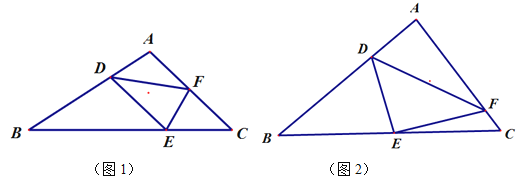
(1)如图1,当DE=DF时,图1中是否存在于AB相等的线段?若存在,请找出并加以证明.若不存在说明理由.
(2)如图2,当DE=kDF(其中0<k<1)时,若∠A=90°,AF=m,求BD的长(用含k,m的式子表示).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com