
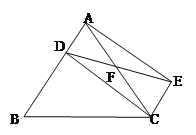
【题目】如图,D是△ABC的边AB上一点,CE∥AB,DE交AC于点F,若FA=FC.
(1)求证:四边形ADCE是平行四边形;
(2)若AE⊥EC,EF=EC=1,求四边形ADCE的面积.
【答案】(1)见解析 (2)![]()
【解析】(1)首先利用ASA得出△DAF≌△ECF,进而利用全等三角形的性质得出CE=AD,即可得出四边形ACDE是平行四边形;
(2)由AE⊥EC,四边形ADCE是平行四边形,可推出四边形ADCE是矩形,由F为AC的中点,求出AC,根据勾股定理即可求得AE,由矩形面积公式即可求得结论.
(1) ∵CE∥AB,
∴∠EDA=∠DEC.
∵FA=FC ∠DFA=∠CFE,
∴△ADF≌△CEF(ASA) ,
∴AF=CF,
∴四边形ADCE是平行四边形;
(2)∵AE⊥EC,
综合(1)四边形ADCE是平行四边形,
∴四边形ADCE是矩形,
∴DE=2EF=2 ∠DCE=![]() ,
,
∴DC=![]() ,
,
四边形ADCE的面积=CE·DC=![]() .
.


 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程x2﹣4x﹣m2=0
(1)求证:该方程有两个不等的实根;
(2)若该方程的两个实数根x1、x2满足x1+2x2=9,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】平面内,如图,在ABCD中,AB=10,AD=15,tanA= ![]() ,点P为AD边上任意点,连接PB,将PB绕点P逆时针旋转90°得到线段PQ.
,点P为AD边上任意点,连接PB,将PB绕点P逆时针旋转90°得到线段PQ.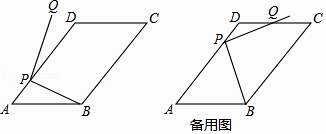
(1)当∠DPQ=10°时,求∠APB的大小;
(2)当tan∠ABP:tanA=3:2时,求点Q与点B间的距离(结果保留根号);
(3)若点Q恰好落在ABCD的边所在的直线上,直接写出PB旋转到PQ所扫过的面积.(结果保留π)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,正方形ABCD中,E为BC上一点,过B作BG⊥AE于G,延长BG至点F使∠CFB=45°
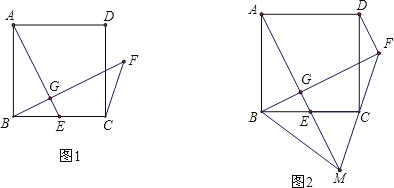
(1)求证:AG=FG;
(2)如图2延长FC、AE交于点M,连接DF、BM,若C为FM中点,BM=10,求FD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A、M、B、N、C在同一直线上顺次排列,点M是线段AB的中点,点N是线段MC的中点,点N在点B的右边.
![]()
(1)填空:图中共有线段 条;
(2)若AB=6,MC=7,求线段BN的长;
(3)若AB=a,MC=7,将线段BN的长用含a的代数式表示出来.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在数轴上,点A表示1,现将点A沿x轴做如下移动,第一次点A向左移动2个单位长度到达点 A1,第二次将点A1,向右移动4个单位长度到达点A2,第三次将点A2向左移动6个单位长度到达点A3,按照这种移动规律移动下去,第n次移动到点An,如果点An与原点的距离等于19,那么n的值是__.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,弦CD⊥AB于点G,点F是CD上一点,且满足 ![]() ,连接AF并延长交⊙O于点E,连接AD、DE,若CF=3,AF=4.
,连接AF并延长交⊙O于点E,连接AD、DE,若CF=3,AF=4. 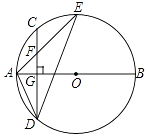
(1)求证:△ADF∽△AED;
(2)求FG的长;
(3)求tan∠E的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com