
【题目】如图1,正方形ABCD中,E为BC上一点,过B作BG⊥AE于G,延长BG至点F使∠CFB=45°
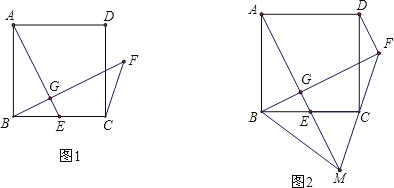
(1)求证:AG=FG;
(2)如图2延长FC、AE交于点M,连接DF、BM,若C为FM中点,BM=10,求FD的长.
【答案】(1)证明见解析;(2)2![]() .
.
【解析】
试题分析:(1)过C点作CH⊥BF于H点,根据已知条件可证明△AGB≌△BHC,所以AG=BH,BG=CH,又因为BH=BG+GH,所以可得BH=HF+GH=FG,进而证明AG=FG;
(2)过D作DQ⊥MF交MF延长线于Q,根据全等三角形的性质和等腰三角形的性质即可求出FD的长.
试题解析:(1)过C点作CH⊥BF于H点,
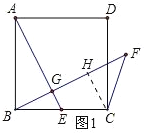
∵∠CFB=45°
∴CH=HF,
∵∠ABG+∠BAG=90°,∠FBE+∠ABG=90°
∴∠BAG=∠FBE,
∵AG⊥BF,CH⊥BF,
∴∠AGB=∠BHC=90°,
在△AGB和△BHC中,
∵∠AGB=∠BHC,∠BAG=∠HBC,AB=BC,
∴△AGB≌△BHC,
∴AG=BH,BG=CH,
∵BH=BG+GH,
∴BH=HF+GH=FG,
∴AG=FG;
(2)∵CH⊥GF,
∴CH∥GM,
∵C为FM的中点,
∴CH=![]() GM,
GM,
∴BG=![]() GM,
GM,
∵BM=10,
∴BG=2![]() ,GM=4
,GM=4![]() ,
,
∴AG=4![]() ,AB=10,
,AB=10,
∴HF=2![]() ,
,
∴CF=2![]() ×
×![]() =2
=2![]() ,
,
∴CM=2![]() ,
,
过B点作BK⊥CM于K,
∵CK=![]() CM=
CM=![]() CF=
CF=![]() ,
,
∴BK=3![]() ,
,
过D作DQ⊥MF交MF延长线于Q,
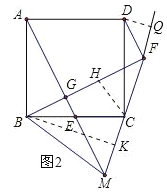
∴△BKC≌△CQD
∴CQ=BK=3![]() ,
,
DQ=CK=![]() ,
,
∴QF=3![]() -2
-2![]() =
=![]() ,
,
∴DF=![]() =2
=2![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,△ABC中,E为BC边的中点,CD⊥AB,AB=2,AC=1,DE= ![]() ,则∠CDE+∠ACD=( )
,则∠CDE+∠ACD=( ) 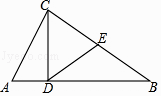
A.60°
B.75°
C.90°
D.105°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】列方程解应用题
(1)为了迎接新年的到来,学校准备向每位同学赠送一张贺年卡,甲、乙两家都可以印制这种贺年卡,甲厂要收制版费600元,且印制每张0.35元,乙厂要收制版费500元,且印制每张0.40元,两厂制作的贺年卡的质量一样.
①当印制多少张时,甲、乙两厂的收费一样?
②如果要印制2500张,选择哪一家合算?
③根据你的计算和判断,你认为印制多少张时,选择甲厂更合算?印制多少张时,选择乙厂更合算?
(2)我校每天中午总是在规定时间打开学校大门,七年级新生小明每天中午同一时间从家骑自行车到学校,星期一中午他以每小时15千米的速度到校,结果在校门口等了6分钟才开门,星期二中午他以每小时9千米的速度到校,结果校门刚好已开了6分钟,星期三中午小明想准时到达学校门口,那么小明骑自行车的速度应该为每小时多少千米?
根据下面思路,请完成此题的解答过程:
解:设星期三中午小明从家骑自行车准时到达学校门口所用时间为t小时,则星期一中午小明从家骑自行车到达学校门口所用时间为 小时,星期二中午小明从家骑自行车到达学校门口所用时间为 小时,由题意列方程得:

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某开发公司生产的960件新产品,需要精加工后,才能投放市场。现有甲、乙两个工厂都想加工这批产品,已知甲工厂单独加工完这批产品比乙工厂单独加工完这批产品多用20天,而乙工厂每天比甲工厂多加工8件产品,公司需付甲工厂加工费用每天80元,乙工厂加工费用每天120元。
(1)求甲、乙两个工厂每天各能加工多少件新产品。
(2)公司制定产品加工方案如下:可以由每个厂家单独完成;也可以由两个厂家同时合作完成。在加工过程中,公司需派一名工程师每天到厂进行技术指导,并负担每天5元的误餐补助费。 请你帮助公司选择一种既省时又省钱的加工方案,并说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
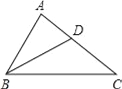
【题目】如图,在△ABC中,BD平分∠ABC,∠A=2∠C.
(1)若∠C=38°,则∠ABD= ;
(2)求证:BC=AB+AD;
(3)求证:BC2=AB2+ABAC.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】填空或填写理由.
(1)如图甲,∵∠ =∠ (已知);
∴AB∥CD( )
(2)如图乙,已知直线a∥b,∠3=80°,求∠1,∠2的度数.
解:∵a∥b,( )
∴∠1=∠4( )
又∵∠3=∠4( )
∠3=80°(已知)
∴∠1=( )(等量代换)
又∵∠2+∠3=180°
∴∠2=( )(等式的性质)

查看答案和解析>>
科目:初中数学 来源: 题型:
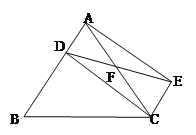
【题目】如图,D是△ABC的边AB上一点,CE∥AB,DE交AC于点F,若FA=FC.
(1)求证:四边形ADCE是平行四边形;
(2)若AE⊥EC,EF=EC=1,求四边形ADCE的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(11·湖州)(本小题10分)
如图,已知E、F分别是□ABCD的边BC、AD上的点,且BE=DF。
⑴求证:四边形AECF是平行四边形;
⑵若BC=10,∠BAC=90°,且四边形AECF是菱形,求BE的长。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示的圆柱形容器的容积为81升,它的底面直径是高的2倍.(π取3)
(1)这个圆柱形容器的底面直径为多少分米?
(2)若这个圆柱形容器的两个底面与侧面都是用铁皮制作的,则制作这个圆柱形容器需要铁皮多少平方分米?(不计损耗)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com